Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Что и требовалось доказать
|
|
Следствие. (Формула Муавра). Если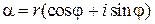 
и nÎN, то
.
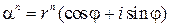Доказательство. Достаточно в теореме положить 
и умножить последовательно число 
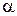само на себя n раз.
Пример. (-1+i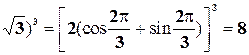 
Аналогично доказывается формула:
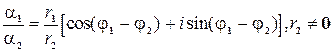
Определение. Корнем натуральной степени n из комплексного числа 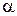(обозначается 
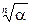) называется комплексное число 
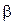такое, что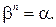 
Теорема. (Извлечение корня) Корень степени n из комплексного числа 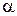имеет n значений, определяемых по формуле:
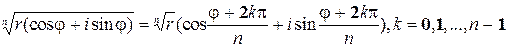
Доказательство. По определению корня имеем: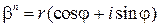 
. Положим 
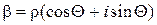. Тогда 
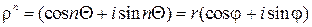. Откуда 
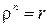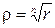или 
и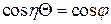 
; следовательно n 
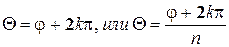. В силу периодичности функций sin и cos значения 
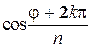и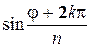 
будут различны при 
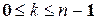, что и требовалось доказать.
Пример. Решить уравнение: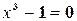 
,
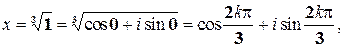
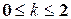
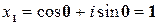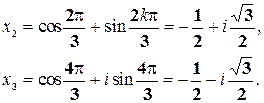
Задание 1. Показать, что число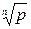 
, p - простое число, n>1 иррационально.
Задание 2. Сравнить числа: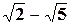 
и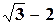 
.
Задание 3. Доказать, что:
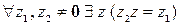
(число z называется частным от деления z 1 на z2 и обозначается символом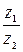 
)
Задание 4. Доказать равенство и выяснить его геометрический смысл:
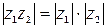
Задание 5. Доказать, что величина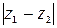 
равна расстоянию на комплексной плоскости между точкам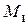и 
и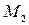 
, изображающими комплексные числа z 1 и z2.
Date: 2015-07-02; view: 637; Нарушение авторских прав