
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Многочлен в комплексной области. Теорема Безу. Основная теорема алгебры
|
|
Рассмотрим комплекснозначные функции комплексной переменной 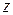 , имеющей вид:
, имеющей вид:
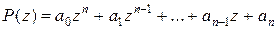 (6)
(6)
где 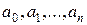 - заданные комплексные числа
- заданные комплексные числа 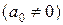 . Такие функции называются многочленами n-й степени. Комплексное число
. Такие функции называются многочленами n-й степени. Комплексное число 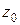 называется корнем (или нулем) многочлена
называется корнем (или нулем) многочлена 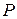 , если
, если 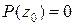 .
.
Справедливо следующее утверждение.
Теорема (теорема Безу). Комплексное число 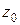 является корнем многочлена
является корнем многочлена 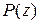 тогда и только тогда, когда существует такой многочлен
тогда и только тогда, когда существует такой многочлен 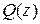 , что
, что
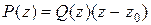 . (7)
. (7)
Доказательство. Из школьного курса алгебры известно, что всякий многочлен 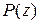 можно разделить на любой многочлен
можно разделить на любой многочлен 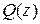 с остатком. Это значит, что для любых многочленов
с остатком. Это значит, что для любых многочленов 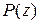 и
и 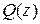 существуют такие многочлены
существуют такие многочлены 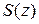 и
и 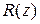 , что
, что
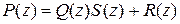 (8)
(8)
причем степень многочлена 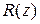 меньше степени многочлена
меньше степени многочлена 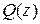 (представление
(представление 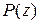 в виде (8) получается при делении
в виде (8) получается при делении 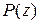 на
на 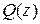 «углом»). В школьном курсе рассматриваются многочлены с действительными коэффициентами, однако аналогичное утверждение справедливо и для многочленов с комплексными коэффициентами.
«углом»). В школьном курсе рассматриваются многочлены с действительными коэффициентами, однако аналогичное утверждение справедливо и для многочленов с комплексными коэффициентами.
Для случая 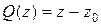 формула (8) примет вид
формула (8) примет вид
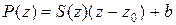 (9)
(9)
здесь 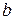 - многочлен, степень которого меньше единицы (степени
- многочлен, степень которого меньше единицы (степени 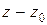 ), т.е. постоянное число. Полагая в равенстве (9)
), т.е. постоянное число. Полагая в равенстве (9) 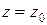 , получим
, получим
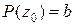 (10)
(10)
Итак, если 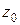 - корень
- корень 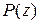 , т.е.
, т.е. 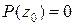 , то и
, то и 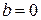 и формула (9) совпадает с (7). Обратно, если
и формула (9) совпадает с (7). Обратно, если 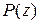 делится без остатка на
делится без остатка на 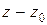 , то
, то 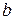 в формуле (9) равно нулю и в силу равенства (10) имеем
в формуле (9) равно нулю и в силу равенства (10) имеем 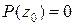 .
.
Лемма (условие тождественности двух многочленов). Две функции
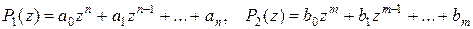 (11)
(11)
совпадают тогда и только тогда, когда 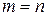 и
и 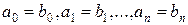 .
.
Теорема (основная теорема алгебры). Всякое уравнение вида
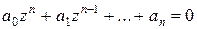 ,
,
где 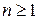 , а
, а 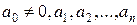 - комплексные числа, имеет решения в поле
- комплексные числа, имеет решения в поле 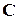 комплексных чисел.
комплексных чисел.
Date: 2015-07-02; view: 2535; Нарушение авторских прав