Легко проверить, что для сложения и умножения комплексных чисел справедливы коммутативный, ассоциативный и дистрибутивный законы

Комплексные числа, их изображение на плоскости. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа.

Комплексные числа были введены в математику в середине 16 века в связи с решениями квадратных и кубических уравнений. Их вве­дение дало возможность решить уравнение x²+1=0.

Комплексные числа нашли применение в самых различных об­ластях науки и техники, в том числе в электротехнике и аэрогидроди­намике.

Определение. Точки числовой плоскости R² называются ком­плексными числами, если равенство, сложение и умножение точек определены следующим образом:

1).(a,b)=(c,d) тогда и только тогда, когда a=c, b=d;

2). (a,b)+(c,d)= (a+c,b+d);

3). (a,b)(c,d)=(ac-bd,ad+bc).

Множество R² при этом называется множеством ком­плекс­ных чисел или комплексной плоскостью и обо­значается бук­вой С.

Под точкой (а,0), лежащей на оси абсцисс, как и прежде, будем пони­мать вещественное число а, то есть а=(а,0).

Ясно, что для вещественных чисел выполняются условия 1)-3) (проверить); следовательно, R 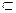C, то есть всякое вещественное число явля­ется и комплексным.

Точка i=(0,1) называется мнимой единицей. Из условия 3) сле­дует основное в теории комплексных чисел равенство i²=-1, так как

i²=(0,1)(0,1)=(1,0)=-1.

Легко проверить, что для сложения и умножения комплексных чисел справедливы коммутативный, ассоциативный и дистрибутивный законы.

Покажем, что любое комплексное число z=(x,y) можно предста­вить в виде арифметической комбинации из действительных чисел x и y и мнимой единицы i:

(x,y)=(x,0)+(0,y)=(x,0)+(0,1)(0,y)=x+iy.

Двучлен x+iy называется алгебраической формой ком­плексного числа (x,y); число х называется действительной ча­стью, а y - мнимой частью комплексного числа z=(x,y)=x+iy; при этом ис­пользуются обозначения:

x=Rez, y=Imz.

Свойства 1).-3)., отнесенные к алгебраической форме комплекс­ного числа, выглядят более привычно:

1). a+ib=c+id тогда и только тогда, когда действительная и мнимая части первого числа равны соответственно действительной и мнимой части второго числа;

2). (a+ib)+(c+id)=(a+c)+i(b+d), то есть чтобы сложить два комплекс­ных числа, нужно сложить соответственно их действительные и мни­мые части;

3). (a+ib)(c+id)=(ac-bd)+i(ad+bc), то есть умножение комплексных чи­сел производится по правилу умножения двучлена на двучлен с доба­воч­ным условием i²=-1.

4). (a+ib)-(c+id)=(a-c)+i(b-d), то есть чтобы найти разность двух ком­плексных чисел, нужно соответственно из действительной и мнимой частей уменьшаемого вычесть действительную и мнимую части вычи­таемого.

5).Частным комплексных чисел z₁ и z₂ называется такое комплексное число z= 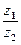, что z₁=zz₂.

Пусть z₁=c+id, z₂=a+ib, z=x+iy. Тогда c+id=(x+iy)(a+ib).

Пользуясь свойствами 3) и 1), найдем это частное:

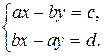
Решив систему, получим:

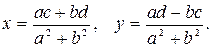
Итак,

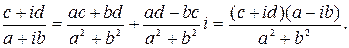(1)

Пусть 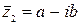. Тогда z₂ 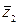=a²+b². Поэтому формулу (1) можно запи­сать в виде

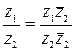
Определение. Число a-ib называется сопряженным числу a+ib.

Пример.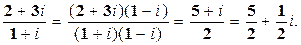

Из выше сказанного вытекает: множество С - это поле, являющееся расширением поля действительных чисел R, в котом каждый элемент z=(x,y) представим в виде z=x+iy, где i²=-1.

Выберем на плоскости R² декартову прямоугольную систему ко­орди­нат XOY

При геометрическом изображении комплексных чисел 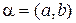ось OX называют действительной осью, ось OY - мнимой осью, а сис­тема ко­ординат ХОY - комплексной плоскостью. Обозначим через r длину радиус-вектора точки (a,b) и через 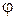- угол, образованный им с положительным направлением действительной оси (рис.1). Ясно, что

a=r cos 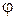b=r sin 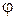r=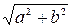

Рис. 1

Откуда

(a+b)=a+bi=r(cos 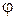+i sin 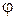), (2)

Где

cos 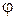= 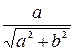, а sin = .

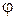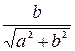Число r = 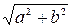называется модулем комплексного числа 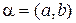и обозначается символом 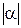; угол 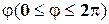называется ар­гументом комплексного числа 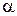и обозначается символом arg .

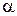Правая часть равества (2) называется тригонометрической формой комплексного числа a+bi.

Пример 1. Представить в тригонометрической форме:

, ,

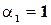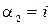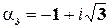
а) 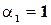; 1=1+Oi; r=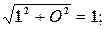

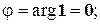
1=cos0+isin0

б) 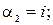i=o+1i; r=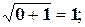

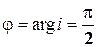
i = cos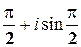

в) 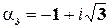-1+i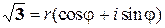

r=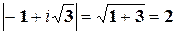

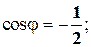
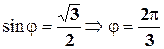
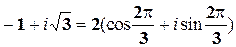
Date: 2015-07-02; view: 923; Нарушение авторских прав