Комплексные числа. 1. Понятие комплексного числа

1. Понятие комплексного числа. Из школьного курса математики известно, что действительных чисел недостаточно для решения квадратных уравнений. Простейшее из квадратных уравнений 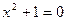не имеет корней среди действительных чисел. Попробуем расширить систему действительных чисел до такой системы чисел, чтобы это уравнение имело решение.

Выберем на плоскости прямоугольную систему координат с осью абсцисс 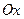и осью ординат 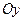. Будем обозначать 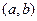точку с абсциссой 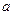и ординатой 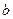. Определим на множестве точек плоскости (другими словами, на упорядоченных парах действительных чисел) операции сложения и умножения следующим образом:

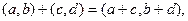
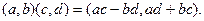
Заметим, что

,

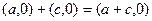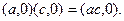
Поэтому точки, лежащие на оси 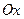можно считать точками действительной оси, и мы не будем различать точку 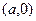и действительное число .

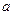Кроме того,

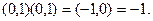
Традиционно эту точку обозначают буквой .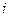

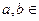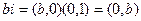Учитывая, что для R и 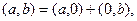получаем:

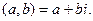
В этой записи операции сложения и умножения выглядят так:

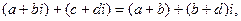
т.е. эти операции выполняются как с обычными двучленами с учетом равенства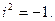

Пусть дано число 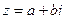. Назовем число 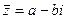сопряженным числу 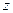. Заметим, что

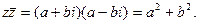
Определив операции сложения и умножения, естественно ввести обратные операции вычитания и деления:

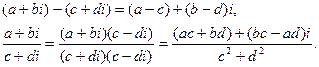
Последняя формула довольно громоздка, и запоминать ее не стоит. Следует только знать, что для вычисления дроби нужно числитель и знаменатель умножить на сопряженное знаменателю число.

Итак, построенная система чисел с алгебраическими операциями называется множеством комплексных чисел и обозначается С.

2. Тригонометрическая форма записи комплексного числа. Форма записи комплексного числа 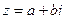называется алгебраической. Число 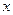называется действительной частью комплексного числа 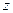, 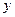- мнимой частью. Обозначение:

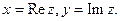
Кроме этой формы существует другая – тригонометрическая. Сначала введем некоторые понятия.

Модулем комплексного числа называется неотрицательное действительное число

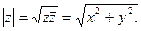
Геометрический смысл модуля прост – это расстояние от начала координат до точки плоскости, соответствующей комплексному числу .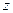

Аргументом 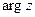комплексного числа 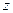называют угол между положительным направлением оси 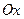и радиус-вектором точки 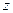(отсчитываемый в положительном направлении):

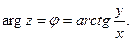
Аргумент может принимать любые значения, но при заданном модуле углы, отличающиеся на 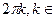Z, соответствуют одному и тому же числу .

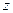Для числа 0 аргумент не определен.

Действительная и мнимая части комплексного числа связаны с модулем и аргументом очевидными соотношениями:

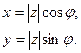
Тогда

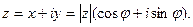
Это и есть тригонометрическая форма записи комплексного числа .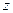

Заметим, что операции сложения и вычитания выглядят в алгебраической форме просто и естественно, но формулы для умножения и деления кажутся весьма громоздкими. Если же мы перейдем к тригонометрической форме записи комплексного числа, то получим:

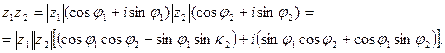
Итак, модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов сомножителей.

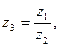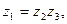Несложно показать, что при делении модули делятся, а аргументы вычитаются: так как то поэтому и 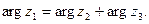Значит, 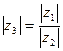и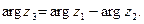

3. Возведение комплексного числа в степень и извлечение корня. Из формулы для умножения комплексных чисел в тригонометрической форме сразу же следует формула для возведения комплексного числа в степень – формула Муавра:

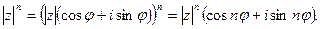
Теперь попробуем извлечь из комплексного числа корень произвольной степени. В отличие от действительных чисел это всегда возможно. Пусть дано комплексное число 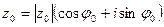. Мы должны найти такое комплексное числ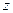о ,что 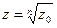, т.е. 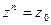. Это означает, что 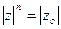и 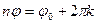. Отсюда 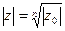и 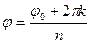. Если при одном и том же модуле аргументы отличаются на 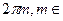Z, то они определяют одно и то же комплексное число. Значит, различные корни мы получим, когда 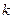пробегает числа 0,1,… 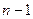. Остальные значения 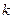новых корней не дадут.

Геометрически это выглядит так: корни 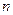-й степени из комплексного числа 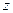находятся на окружности с центром в начале координат радиуса 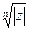в вершинах правильного 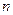-угольника.

4. Важное замечание. Мы расширили систему действительных чисел с целью иметь возможность решить уравнение 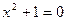и, как следствие, все квадратные уравнения. Как мы видим, в построенной системе комплексных чисел можно еще и извлекать корни любой степени, т.е.решать алгебраические уравнения вида 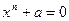. Оказывается, произвольный многочлен с комплексными коэффициентами имеет комплексный корень, более того, он имеет ровно 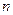комплексных корней с учетом их кратностей. Это утверждение называется основной теоремой алгебры, но доказательство этой теоремы выходит за рамки нашего курса.

Date: 2015-07-02; view: 585; Нарушение авторских прав