
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комплексные числа и арифметические действия над ними
|
|
КОМПЛЕКСНЫЕ ЧИСЛА
Различают прямые и обратные действия (операции) над числами. Например, сложению соответствует обратная операция - вычитание, умножению - деление, возведению в целую положительную степень - извлечение корня.
Обратные операции приводят к необходимости постепенного расширения понятия числа. Так, действительных чисел недостаточно для того, чтобы извлечь корень четной степени из отрицательного числа. Следовательно, действительных чисел недостаточно даже для того, чтобы решить любое квадратное уравнение, например, 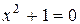 .
.
Этот и прочие вопросы математики приводят к необходимости расширения множества действительных чисел до множества так называемых комплексных чисел.
Геометрическим образом действительного числа является точка прямой. Мы введем такое множество чисел, геометрическими образами которых будут точки плоскости, а множество действительных чисел будет входить в это множество как подмножество.
Определение. Комплексным числом называется символ 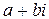 , где a и b действительные числа. a называется действительной частью, а b мнимой частью комплексного числа, число i определяется таким образом
, где a и b действительные числа. a называется действительной частью, а b мнимой частью комплексного числа, число i определяется таким образом 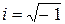 и называется мнимой единицей.
и называется мнимой единицей.
Символ 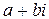 будем пока что рассматривать как цельный.
будем пока что рассматривать как цельный.
Множество действительных чисел входит в множество комплексных чисел с помощью условия
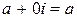 . (1)
. (1)
Комплексные числа 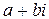 и
и 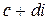 считаются равными[1] одно другому тогда и только тогда, когда
считаются равными[1] одно другому тогда и только тогда, когда 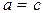 и
и 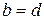 . В частности,
. В частности, 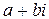 = 0 тогда и только тогда, когда
= 0 тогда и только тогда, когда 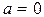 и
и 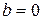 . Действительно, из равенства (1) вытекает
. Действительно, из равенства (1) вытекает 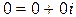 .
.
Введем над комплексными числами арифметические операции так, чтобы они при применении к действительным числам давали бы те же результаты, как и в арифметике действительных чисел.
1) Операцию сложения двух комплексных чисел 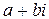 и
и 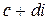 определим равенством
определим равенством
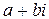 +
+ 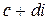 =
= 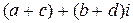 .
.
Применяя это определение к действительным числам, получаем
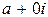 +
+ 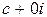 =
= 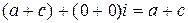 ,
,
то есть это определение не противоречит сложению действительных чисел.
2) Операцию умножения двух комплексных чисел определим равенством
(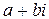 )(
)(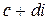 ) =
) = 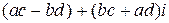 .
.
Применяя это определение к действительным числам, получим
(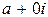 )(
)(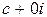 ) =
) = 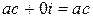 .
.
Это определения также не противоречит умножению действительных чисел.
Легко показать, что для операций сложения и умножения комплексных чисел справедливые все пять законов арифметики:
1.  (переместительное свойство сложения);
(переместительное свойство сложения);
2. 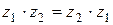 (переместительное свойство умножения);
(переместительное свойство умножения);
3. 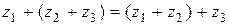 (соединенное свойство сложения);
(соединенное свойство сложения);
4. 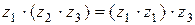 (соединенное свойство умножения);
(соединенное свойство умножения);
5. 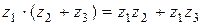 (распределительное свойство умножения),
(распределительное свойство умножения),
где 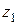 ,
, 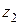 ,
, 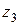 - комплексные числа.
- комплексные числа.
В операциях над комплексными числами особую роль играет число 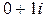 , которое определяют просто как i. Если возвести это число в квадрат, получим
, которое определяют просто как i. Если возвести это число в квадрат, получим 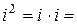
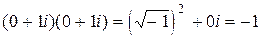 и, таким образом,
и, таким образом, 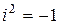 .
.
Произведение действительного числа 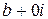 и мнимой единицы
и мнимой единицы 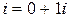 называют мнимым числом и обозначают через
называют мнимым числом и обозначают через 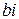 , то есть
, то есть 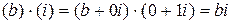 .
.
Всякое комплексное число 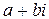 можно рассматривать как сумму числа a и произведения
можно рассматривать как сумму числа a и произведения 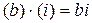 , то есть как сумму действительного числа a и мнимого числа
, то есть как сумму действительного числа a и мнимого числа 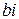 . Действительно,
. Действительно,
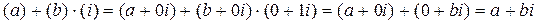 .
.
Используют также обозначение: 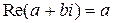 - действительная часть комплексного числа,
- действительная часть комплексного числа, 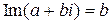 - мысленная часть комплексного числа.
- мысленная часть комплексного числа.
Очевидна также, справедливость таких равенств:
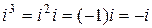 ,
,
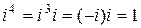 ,
,
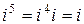 ,
,
и вообще
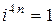 ,
, 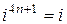 ,
, 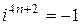 ,
, 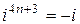 . (2)
. (2)
Замечание. На практике комплексные числа перемножают по правилу умножения двучленов с учетом равенства 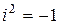 , то есть, (
, то есть, (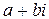 )
) 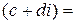
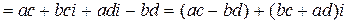 .
.
При возведении в целую положительную степень n комплексного числа 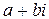 к выражению
к выражению 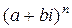 применяют формулу разложения бинома Ньютона, а потом уже используют равенства (2).
применяют формулу разложения бинома Ньютона, а потом уже используют равенства (2).
Пример 1. Вычислить 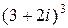 . Имеем:
. Имеем:
.
Два комплексных числа 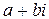 и
и 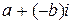 , которые отличаются лишь знаком мнимой части, называются комплексно сопряженными. Для таких чисел выполняются очевидные соотношения:
, которые отличаются лишь знаком мнимой части, называются комплексно сопряженными. Для таких чисел выполняются очевидные соотношения:
(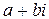 )
) 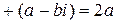 , (
, (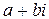 )(
)(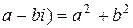 .
.
3) Вычитание определяется как операция обратная сложению, то есть разностью двух чисел 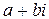 и
и 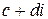 называется такое число
называется такое число 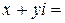
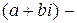
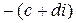 , что
, что
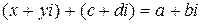 . (3)
. (3)
Покажем, что разность всегда существует и единственна.
На основании определения сложения равенство (3) можно записать так: 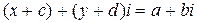 , откуда
, откуда 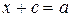 ,
, 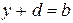 . Итак,
. Итак, 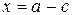 ,
, 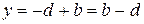 . Таким образом, операция вычитания определяется равенством
. Таким образом, операция вычитания определяется равенством 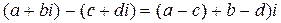 , причем разность определяется однозначно. Действительно, если предположить, что
, причем разность определяется однозначно. Действительно, если предположить, что 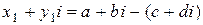 , то отнимая одно представление разности из второго получим
, то отнимая одно представление разности из второго получим 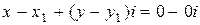 , что означает
, что означает 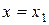 ,
, 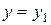 , то есть разность единственна.
, то есть разность единственна.
4) Частным чисел 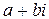 и
и 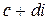 называют такое число
называют такое число 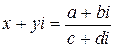 , что произведение чисел
, что произведение чисел 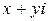 и
и 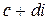 равняется
равняется 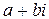 , то есть если
, то есть если
(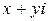 )(
)(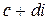 ) =
) = 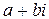 (4)
(4)
Покажем, что частное существует и единственно, если  или c 2 + d 2
или c 2 + d 2 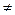 0. Равенство (4) можно переписать так
0. Равенство (4) можно переписать так 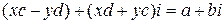 . Из последнего равенства вытекает справедливость уравнений:
. Из последнего равенства вытекает справедливость уравнений: 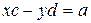 ,
, 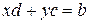 . Решая эти уравнения, получаем:
. Решая эти уравнения, получаем:
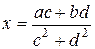 ,
, 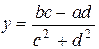 .
.
Таким образом, деления определяется равенством:
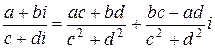 ,
,  ,
,
причем частное определяется однозначно.
Замечание. На практике частное двух комплексных чисел находят так
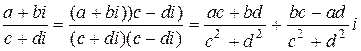 .
.
Справедливая теорема:
Теорема. Если в сумме, разности, произведении и частном каждое комплексное число заменить сопряженным с ним, то и результаты заменятся сопряженными числами, то есть:
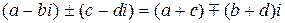 ,
,
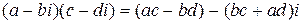 ,
,
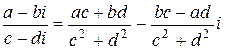 .
.
Доказательство непосредственно вытекает из рассмотрения равенств, которые определяют эти операции.
2. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
 Возьмем на плоскости декартову прямоугольную систему координат Хo. Комплексное число
Возьмем на плоскости декартову прямоугольную систему координат Хo. Комплексное число 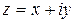 изображают точкой плоскости (х, у) или радиусом-вектором. Между точками плоскости и бесконечным множеством всех комплексных чисел существует взаимно однозначное соответствие.
изображают точкой плоскости (х, у) или радиусом-вектором. Между точками плоскости и бесконечным множеством всех комплексных чисел существует взаимно однозначное соответствие.
Действительные числа откладываются на оси oХ (см. Рис.1), мнимые на оси oУ. Поэтому ось oХ называется действительной осью, а ось oУ мнимой. Началу координат отвечает число ²0².
Кроме декартовой формы комплексного числа очень употребительной является еще одна форма – тригонометрическая.
 Y z = x + iy
Y z = x + iy


 y
y
r
 |
 j
j
0 x X
Рис. 1.
Пусть (х, у) декартовые координаты точки, которая изображает комплексное число 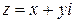 , а
, а 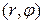 ее полярные координаты. Тогда
ее полярные координаты. Тогда
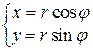 и, итак,
и, итак,
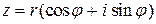 . (5)
. (5)
Выражение (5) называется тригонометрической формой комплексного числа. Величины r и j называются соответственно модулем и аргументом комплексного числа, и обозначают 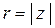 ,
, 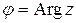 . Модуль комплексного числа определяется однозначно, с помощью формулы
. Модуль комплексного числа определяется однозначно, с помощью формулы 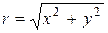 , аргумент для каждого комплексного числа имеет бесконечно большое множество значений, любые два из которых отличаются на число кратное
, аргумент для каждого комплексного числа имеет бесконечно большое множество значений, любые два из которых отличаются на число кратное 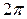 , то есть
, то есть 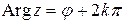 ,
, 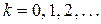 . Обычно используется так называемое главное значение аргумента
. Обычно используется так называемое главное значение аргумента 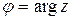 , которое определяется дополнительным условием
, которое определяется дополнительным условием 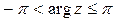 , или
, или 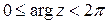 .
.
Аргумент числа нуль – не обусловлен.
Отметим, что аргумент комплексного числа является корнем системы уравнений:
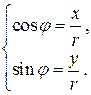
Из этой системы находим 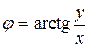 .
.
Пример 2: Представить комплексное число 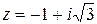 в тригонометрической форме.
в тригонометрической форме.

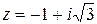 Y
Y



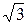

 j
j

-1 X
Мал. 2.
Имеем 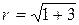 =2,
=2, 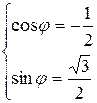 , Можем взять
, Можем взять 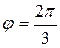 .
.
Итак, 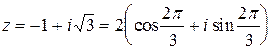 .
.
3. Геометрическое толкование сложения и умножения (теоремы о модулях и аргументах).
1. Пусть даны два комплексных числа  и
и  . Их суммой будет
. Их суммой будет 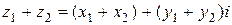 ; Нас будет интересовать геометрическое толкование этого результата.
; Нас будет интересовать геометрическое толкование этого результата.
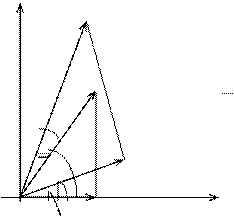
Известно, что при сложении векторов соответствующие проекции их складываются. Ведь вектор, который изображает комплексное число  получается складыванием векторов, которые изображают векторы
получается складыванием векторов, которые изображают векторы 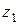 и
и 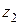 . Из геометрического содержания
. Из геометрического содержания 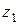 и
и 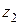 вытекает следующее неравенство для модулей (первая теорема о модулях):
вытекает следующее неравенство для модулей (первая теорема о модулях): 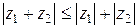 (см. Рис. 3).
(см. Рис. 3).
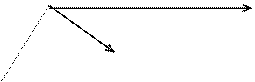
Вычитание можно рассматривать как сложение (см. Рис. 4), то есть 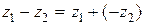 ,
,
Из геометрического содержания вычитания вытекает, что 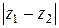 подает собою отстань между точками, которые изображают числа
подает собою отстань между точками, которые изображают числа 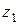 и
и 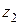 . Отсюда вытекает, что (вторая теорема о модулях)
. Отсюда вытекает, что (вторая теорема о модулях)

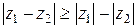
Y
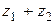
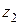
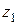





 0
0
X
Рис. 3.
 Y
Y

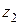




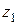
 |
0 X
 |
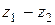
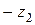
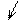
Рис. 4.
.
2. Перемножим теперь два комплексных числа 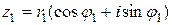 и
и 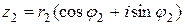 ,
,
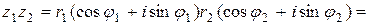
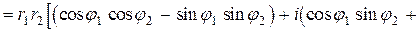
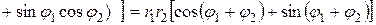 ;
;
Отсюда вытекает, что
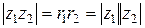 ,
, 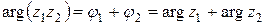 (6),
(6),
то есть (первая теорема о модулях и аргументах) при умножении комплексных чисел модули перемножаются, а аргументы складываются.
Вектор, который изображает 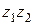 может быть получен из вектора, который изображает число
может быть получен из вектора, который изображает число 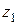 (
(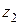 ), поворотом на
), поворотом на 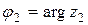 (
(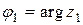 ) и растягиванием в
) и растягиванием в 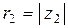 (
(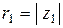 ) раз (см. Мал. 5), или вектор, который изображает
) раз (см. Мал. 5), или вектор, который изображает 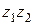 , может быть получен из вектора, который изображает единицу, поворотом на угол
, может быть получен из вектора, который изображает единицу, поворотом на угол 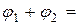
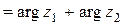 и растягиванием в
и растягиванием в 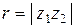 раз (см. Рис. 6).
раз (см. Рис. 6).





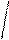


 Y
Y
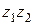

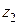
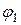

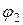

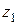
0 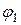 1 X
1 X
Рис. 5.
Y 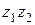
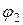
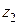
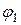
0 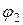 1 X
1 X
Рис. 6.
Формулы (6) можно распространить на любое число сомножителей, то есть: 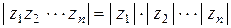 ,
, 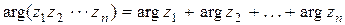 . В частности, если
. В частности, если 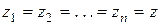 , то
, то 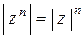 ,
, 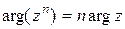 . В результате имеем
. В результате имеем
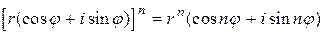 . (7)
. (7)
Это есть так называемая формула Муавра[2].
Поделим два комплексных числа одно на другое. Будем иметь:
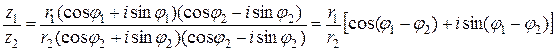 .
.
Итак,
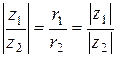 ,
, 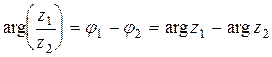 ,
,
то есть (вторая теорема о модулях и аргументах) при делении модули делятся, а аргументы вычитаются.
Отметим, что формула Муавра может иметь место для любого целого показателя, если ввести обозначение: 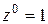 ,
, 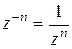 . Действительно,
. Действительно,

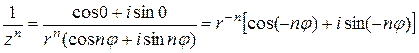 .
.
[1] Понятие больше - меньше для комплексных чисел не определяется.
[2] Муавр (Moivre) Абрахам (1687-1754), англ. математик. По национальности француз. Нашел правило возведения в степень комплексного числа. В теории вероятностей доказал частный случай так называемой теоремы Лапласа
Date: 2015-07-02; view: 1183; Нарушение авторских прав