Корни многочленов

В разделе "Решение квадратных уравнений с вещественными коэффициентами" мы видели, что в поле комплексных чисел любой квадратный трехчлен с вещественными коэффициентами имеет корни, этих корней два, если дискриминант отличен от нуля, и один в противном случае. Теперь, когда мы имеем возможность извлекать корни из комплексных чисел, мы можем найти корни квадратного трехчлена с комплексными коэффициентами, то есть решить уравнение

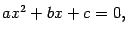
где 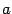, , 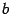-- комплексные числа, .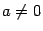

Выполняя те же действия, что и в разделе "Решение квадратных уравнений с вещественными коэффициентами", приходим к уравнению

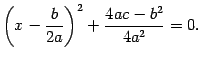
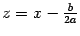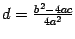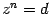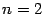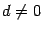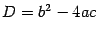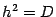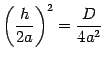Обозначив , , получим уравнение , где . Такое уравнение мы умеем решать. В результате получатся два корня, если , и один, если . Так как тогда и только тогда, когда дискриминант равен нулю, то количество корней определяется тем же условием: равен дискриминант нулю или нет. Кроме того, заметим, что если , то и 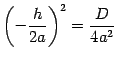. Поэтому корни уравнения 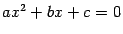можно записать в виде

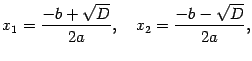
(17.16)

где 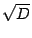означает одно из решений (любое!) уравнения 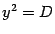. Отметим, что формулы (17.5) также можно записать в виде (17.16), так как при вещественном 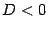выполнено .

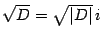Пример 17.10 Решите уравнение .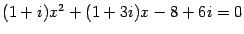

Решение. Находим дискриминант:

Решим уравнение 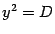. Для этого находим 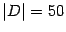. Пусть 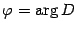. Тогда 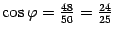. Достаточно найти только одно решение. Второе получим умножением его на 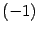. По формуле (17.15)

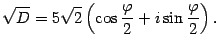
По формулам половинного аргумента с учетом того, что 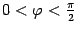, получим

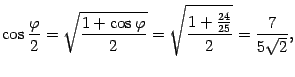
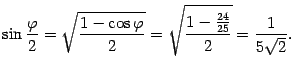
Таким образом, .

По формулам (17.16)

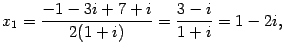
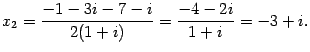
Ответ: , .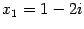

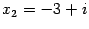Оказывается, что в поле комплексных чисел корни всегда существуют не только у квадратного трехчлена, но и у любого многочлена.

Теорема 17.1 Любой многочлен ненулевой степени с коэффициентами из поля комплексных чисел имеет в этом поле хотя бы один корень.

Данная теорема по традиции называется основной теоремой алгебры. Доказательство ее достаточно сложное и поэтому здесь оно не приводится.

Интересно выяснить, сколько корней имеет многочлен степени 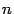. Мы уже знаем, что если 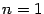, то корень один, если 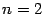, то, как учили в школе, корней два. Кроме того, мы уже выяснили, что многочлен имеет ровно 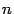различных корней, если .

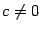Теорема 17.2 Для любого многочлена ненулевой степени в поле комплексных чисел справедливо разложение на множители:

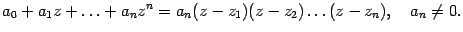
(17.17)

Доказательство пропускаем. Читатель может найти его в [5].

Очевидно, что в указанном разложении числа 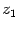, ,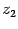..., 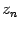являются корнями многочлена и других корней у него быть не может. Однако среди чисел 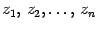могут быть и одинаковые. Поэтому корней может быть меньше, чем 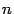. Число одинаковых скобок в разложении (17.17) называется кратностью соответствующего корня. Например, если

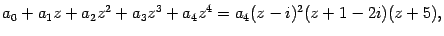
то 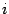-- корень кратности 2, и 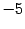-- корни кратности 1 или, иначе, простые корни.

Из предыдущей теоремы легко получить теорему, дающую ответ на вопрос о числе корней многочлена.

Теорема 17.3 В поле комплексных чисел любой многочлен ненулевой степени 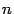имеет ровно 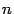корней, если каждый корень считать столько раз, какова его кратность.

По вопросу практического нахождения корней стоит отметить следующее. Для нахождения корней многочленов третьей и четвертой степеней существуют формулы, позволяющие выразить корни многочлена через его коэффициенты. Для многочлена третьей степени -- это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов.

Однако, даже для многочленов третьей и четвертой степени, как правило, корни находят без использования указанных выше формул, так как те дают очень громоздкие выражения. Обычно корни находят приближенно, с помощью различных вычислительных алгоритмов (см. главу 9).

Date: 2015-07-02; view: 969; Нарушение авторских прав