Построение поля комплексных чисел

Из курса школьной математики известно, что любое уравнение 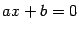имет решение при 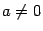. С другой стороны, квадратное уравнение не всегда имеет решение. Например, решения не имеет уравнение 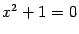. Возникает вопрос, нельзя ли сделать так, чтобы любое квадратное уравнение имело решение?

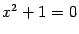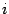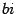Предположим, что уравнение имет решение. Число (абстрактный элемент, не принадлежащий полю вещественных чисел), которое является решением, обозначим буквой , то есть . Мы должны иметь возможность умножать это число на любое вещественное число. Значит, должны появиться числа вида , где 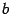-- вещественное число. Для них должна быть возможность сложения с любым вещественным числом. Поэтому должны появиться числа вида .

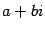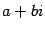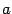Определение 17.1 Числа вида , где и 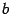-- вещественные числа, называются комплексными числами.

Посмотрим, какие действия арифметики можно производить с комплексными числами. Сложение чисел должно удовлетворять обычным правилам, поэтому:

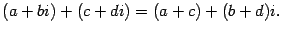
(17.1)

При вычислении произведения скобки раскроем привычным способом:

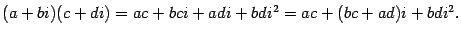
Так как , то получим

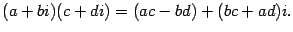
(17.2)

Итак, результаты сложения и умножения комплексных чисел снова оказались комплексными числами. Операцию вычитания определить не сложно:

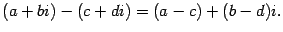
(17.3)

Рассмотрим операцию деления. Учтем, что при умножении числителя и знаменателя дроби на одно и то же число дробь не меняется:

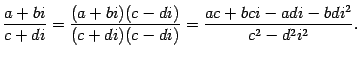
Так как , то

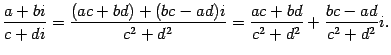
(17.4)

Результат деления двух комплексных чисел оказывается снова комплексным числом. Как видно из полученной формулы, деление нельзя выполнить лишь в том случае, когда 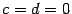, но в этом случае делитель 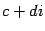тоже равен нулю. Следовательно, невозможно лишь деление на нуль, что соответствует обычным правилам действий с числами.

Итак, мы вроде бы расширили множество вещественных чисел. Но есть в этом построении один существенный пробел. Мы предположили, что есть такое числ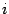о , что . А, может быть, его на самом деле нет?² Чтобы исправить это упущение, используем для построения комплексных чисел уже существующее множество.

Пусть 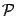-- множество пар вещественных чисел: 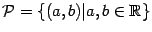. На этом множестве определим операции

1. сложения:

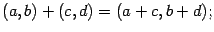
1. вычитания:

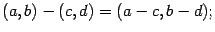
1. умножения:

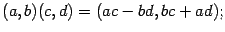
1. деления:

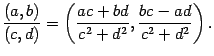
Очевидно, что комплексное число, как оно было определено раньше, -- просто другая форма записи пары вещественных чисел 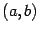, где вместо запятой стоит "+", а второй элемент пары выделяется умножением на букву 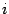. В новой форме записи вещественные числа -- это пары , числу 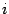соответствует пара 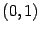, сложение, вычитание, умножение и деление пар чисел и комплексных чисел происходят по одинаковым правилам. Таким образом, комплексные числа стали реально существующим множеством.

Однако в математике, в силу традиции, используется запись комплексного числа 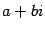, введенная в начале раздела³. Причем принято считать, что

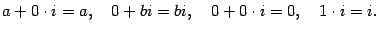
Можно проверить, что комплексные числа образуют поле. В нем обратным элементом к комплексному числу 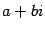служит результат деления 1 на :

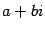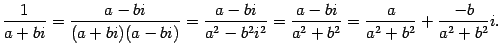
Это поле называется полем комплексных чисел и обозначается .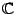

Число 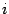называется мнимой единицей, числа 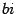-- мнимыми числами. Если 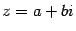, то число 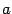называется вещественной частью комплексного числа и обозначается 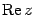, число 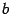называется мнимой частью и обозначается . Число 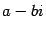называется сопряженным числу 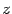и обозначается 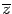, то есть .

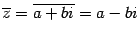Замечание 17.1 В электротехнике, где буква 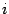обозначает ток, мнимую единицу обозначают буквой .

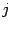Если операции сложения, вычитания и умножения комплексных чисел соответствуют обычным правилам раскрытия скобок, то для выполнения деления нужно или запомнить формулу (17.4), или, что проще, каждый раз при выполнении деления умножать числитель и знаменатель дроби на число, сопряженное знаменателю.

Пример 17.1 Пусть 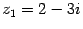, 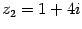. Тогда:

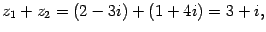
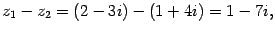
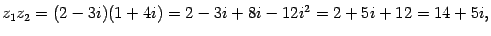
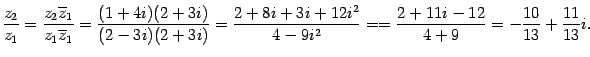
Вычислим еще :

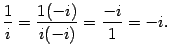
Date: 2015-07-02; view: 2454; Нарушение авторских прав