
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение квадратных уравнений с вещественными коэффициентами
|
|
Вернемся к задаче, поставленной в начале главы: можно ли в поле комплексных чисел решить любое квадратное уравнение (пока только с вещественными коэффициентами)? Для квадратного уравнения 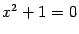 мы одно решение знаем:
мы одно решение знаем: 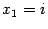 . Очевидно, что
. Очевидно, что  , поэтому
, поэтому  . Следовательно, оба корня такого уравнения известны.
. Следовательно, оба корня такого уравнения известны.
Замечание 17.2 Числа 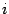 и
и 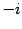 в поле комплексных чисел абсолютно равноправны. Если бы число
в поле комплексных чисел абсолютно равноправны. Если бы число 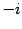 обозначить
обозначить 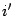 и построить с этим обозначением новое поле комплексных чисел, то оно будет в точности таким же, как и исходное.
и построить с этим обозначением новое поле комплексных чисел, то оно будет в точности таким же, как и исходное.
Рассмотрим уравнение 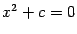 , где
, где  -- вещественное положительное число. Легко проверить, что его корни
-- вещественное положительное число. Легко проверить, что его корни 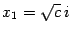 ,
, 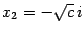 , где
, где 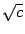 -- обычный арифметический корень.
-- обычный арифметический корень.
Решим уравнение 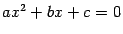 , где
, где  -- вещественные числа,
-- вещественные числа, 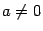 ,
, 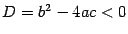 . Для этого выделим в правой части полный квадрат (см. пример 12.1):
. Для этого выделим в правой части полный квадрат (см. пример 12.1):
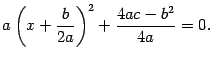
Откуда
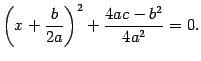
Если  обозначить
обозначить 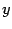 , а
, а 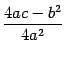 обозначить
обозначить 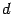 , то получим уравнение предыдущего типа, его решения:
, то получим уравнение предыдущего типа, его решения:
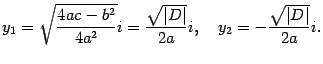
Поэтому
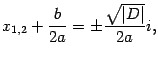
то есть
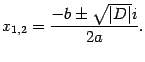
Итак, если дискриминант 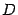 отрицательный, то корни уравнения находятся по формулам:
отрицательный, то корни уравнения находятся по формулам:
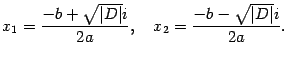
| (17.5) |
Пример 17.2 Решите уравнение 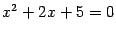 .
.
Решение. Находим дискриминант:

Находим корни:
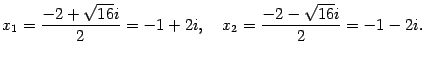
Ответ: 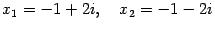 .
.
Date: 2015-07-02; view: 858; Нарушение авторских прав