Тригонометрическая форма комплексного числа. Пусть . Положим , . Из рисунка 17.4 очевидно, что

Пусть 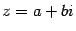. Положим 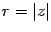, 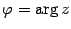. Из рисунка 17.4 очевидно, что

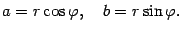
Тогда . Это выражение запишем в виде

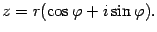
(17.8)

Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде 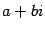называют иногда алгебраической формой комплексного числа.

Отметим, что тригонометрическая форма -- это указание числа по двум его характеристикам: модулю и аргументу. Поэтому вместо формулы (17.8) можно было бы просто записывать пару 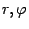, но запись (17.8) принята в силу традиции.

Замечание 17.3 При записи числа в тригонометрической форме НЕЛЬЗЯ вычислять значения 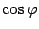и 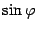, иначе мы потеряем явное указание аргумента 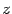и снова вернемся к алгебраической форме. Кроме того, если угол 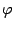получился отрицательным, то знак " " НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.

Пример 17.5 Запишите в тригонометрической форме числа , , , .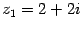

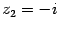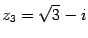Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:

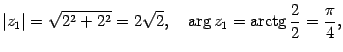
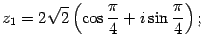
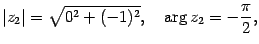
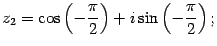
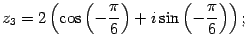
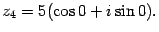
Пусть 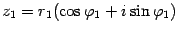, 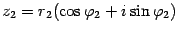. Найдем произведение :

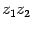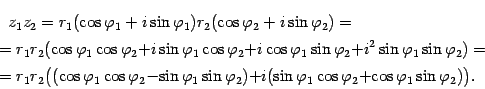
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому

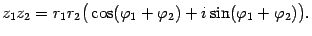
Последняя запись является тригонометрической формой комплексного числа 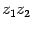. Значит,

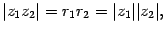
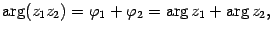
иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Аналогично можно доказать, что

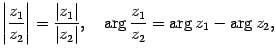
иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.

Несложно проверить, что если 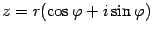, то

Используя правило умножения комплексных чисел в тригонометрической форме, получим формулу для возведения комплексного числа в степень 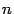, где 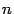-- натуральное число.

Пусть 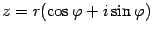. Тогда

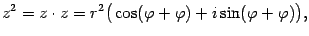
то есть

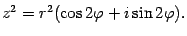
Далее находим

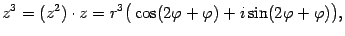
то есть

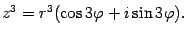
Продолжая умножения дальше, придем к формуле

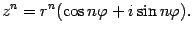
(17.9)

Эта формула называется формулой Муавра.

Пример 17.6 Вычислите 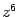, если .

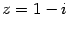Решение. Находим тригонометрическую форму числа :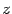

По формуле Муавра

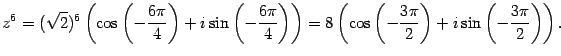
Переходим к алгебраической форме, вычисляя косинус и синус: .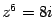

Ответ: .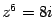

Date: 2015-07-02; view: 532; Нарушение авторских прав