
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Извлечение корня из комплексного числа. Заголовок этого раздела является не совсем точным
|
|
Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения
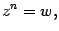
| (17.14) |
где неизвестным служит 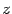 , а
, а 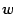 -- известное комплексное число. Но поскольку в школе решение этого уравнения записывалось в виде
-- известное комплексное число. Но поскольку в школе решение этого уравнения записывалось в виде 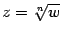 , то, не слишком соблюдая математическую строгость, можно говорить, что мы будем извлекать корень
, то, не слишком соблюдая математическую строгость, можно говорить, что мы будем извлекать корень 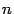 -ой степени из комплексного числа
-ой степени из комплексного числа 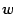 . Итак, решаем уравнение (17.14).
. Итак, решаем уравнение (17.14).
Если 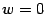 , то
, то 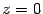 . Пусть
. Пусть 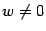 . Запишем число
. Запишем число 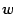 в тригонометрической форме:
в тригонометрической форме: 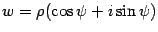 . Здесь
. Здесь 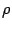 и
и 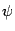 -- известные величины. Запишем неизвестное число
-- известные величины. Запишем неизвестное число 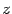 в тригонометрической форме:
в тригонометрической форме: 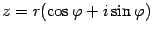 . Здесь
. Здесь 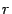 и
и 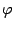 -- неизвестны. По формуле Муавра
-- неизвестны. По формуле Муавра
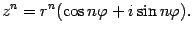
Таким образом,
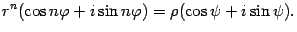
Если два комплексных числа равны, то их модули должны быть равны. Поэтому 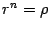 . В этом соотношении
. В этом соотношении 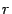 и
и 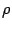 -- положительные числа, следовательно
-- положительные числа, следовательно 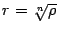 , где справа стоит обычный арифметический корень из положительного числа.
, где справа стоит обычный арифметический корень из положительного числа.
Если два комплексных числа равны, то аргументы у них могут различаться только на величину, кратную 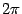 . Поэтому
. Поэтому 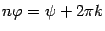 ,
, 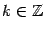 . Отсюда находим, что
. Отсюда находим, что
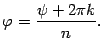
В итоге получили:
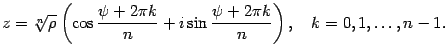
| (17.15) |
Значения  , отличные от указанных в этой формуле, дадут те же значения
, отличные от указанных в этой формуле, дадут те же значения 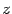 , которые можно получить при
, которые можно получить при 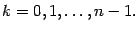
Пример 17.9 Найдите корни уравнения 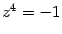 .
.
Решение. Запишем число 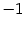 в тригонометрической форме:
в тригонометрической форме:
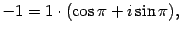
то есть  ,
,  . Тогда
. Тогда
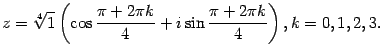
При  получим:
получим:

При 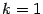 получим:
получим:
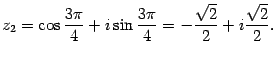
При 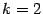 получим:
получим:
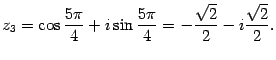
При  получим:
получим:
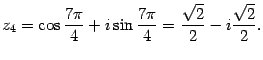
Ответ:  ,
, 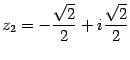 ,
, 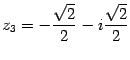 ,
, 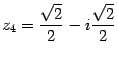 .
.
Date: 2015-07-02; view: 601; Нарушение авторских прав