
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комплексные числа. Действия над ними
|
|
Введение
Методические указания содержат материалы для практических занятий по действиям с комплексными числами и операционному исчислению. Введение комплексных чисел связано с решением уравнений вида х 2 + 1 = 0. В множестве R не существует решений данного уравнения, однако в множестве комплексных чисел – С решение существует. Множество С содержит элемент, квадрат которого равен (-1). Так как этот элемент не может быть действительным, то его обозначают через i, т. е. i 2 = - 1.
Комплексные числа находят широкое применение в задачах физики, геометрии, электротехники. Операционное исчисление изобретено английским ученым О. Хевисойдом, предназначено для решения, дифференциальных уравнений и систем линейных дифференциальных уравнений с постоянными коэффициентами как однородных так и неоднородных. Многие прикладные задачи описываются такими уравнениями. В частности, методы операционного исчисления позволяют с большим успехом рассчитывать любые процессы в сложных электрических цепях при произвольном внешнем напряжении
Методические указания предназначены для студентов 3 факультета, а также для преподавателей.
Комплексные числа. Действия над ними
Комплексное число z - это число вида z = x + iy (алгебраическая форма комплексного числа), где х, у называются соответственно действительной и мнимой частями комплексного числа z и обозначаются х = Re z, y = Im z. Число  называется сопряженным к числу
называется сопряженным к числу  .
.
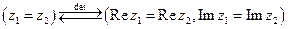
Комплексное число z = x + iy изображается в плоскости ХОУ точкой М с координатами (х, у) или вектором с координатами (х, у), (рис. 1.1)
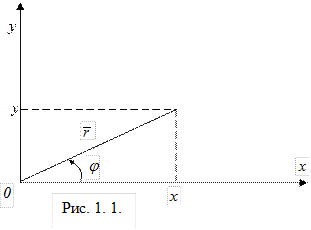
Длина r вектора z называется модулем числа z и обозначается  . Угол j между положительным направлением оси ОХ и вектором z называет аргументом комплексного числа и обозначается Arg z; он определяется с точностью до слагаемого, кратного
. Угол j между положительным направлением оси ОХ и вектором z называет аргументом комплексного числа и обозначается Arg z; он определяется с точностью до слагаемого, кратного 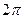 . Значение arg z аргумента z, удовлетворяющее условию
. Значение arg z аргумента z, удовлетворяющее условию 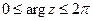 или
или 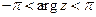 называется главным. Имеем
называется главным. Имеем 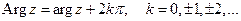
Тригонометрическая и показательная формы комплексного числа имеют вид  .
.
Связь между алгебраической и тригонометрической формами устанавливается при помощи формул 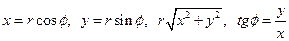 .
.
Действия на комплексными числами осуществляются по следующим правилам
а) числа заданы в алгебраической форме:

б) числа заданы в тригонометрической форме:

Задача 1.
Задана комплексные числа: а)  ; б)
; б) 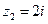 ; в)
; в) 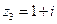 ; г)
; г)  ; д)
; д)  ; е)
; е) 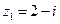 .
.
Представить z 1, z 2, z 3 в тригонометрической, а z 4, z 5, z 6 – в показательной форме и изобразить точками на комплексной площади.
Решение:
а) имеем (см. рис. 1.2) r = 1; j = p,  (1.1)
(1.1)
б) имеем (см. рис. 1.2) r = 2;  ,
,  ;
;
в) имеем  ; согласно рис. 1.2 точка z 3 принадлежит первому квадранту, поэтому
; согласно рис. 1.2 точка z 3 принадлежит первому квадранту, поэтому 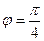 , так что
, так что 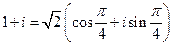 (1.2);
(1.2);

рис. 1.2
г) имеем 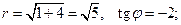 согласно рис. 1.2, точка z 4 принадлежит второму квадранту, поэтому
согласно рис. 1.2, точка z 4 принадлежит второму квадранту, поэтому  так что
так что  ;
;
д) имеет 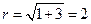 ,
, 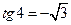 , согласно рис. 1.2, точка z 5 принадлежит третьему квадранту, поэтому
, согласно рис. 1.2, точка z 5 принадлежит третьему квадранту, поэтому 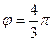 , так что
, так что  (1.3);
(1.3);
е) имеем 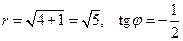 , согласно рис. 1.2, точка z 6 принадлежит четвертому квадранту, поэтому
, согласно рис. 1.2, точка z 6 принадлежит четвертому квадранту, поэтому  .
.
Задача 2.
Найти все значения корней: а) 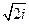 ; б)
; б) 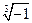 ; в)
; в)  .
.
Решение:
а) имеем согласно (1.2)

б) имеем согласно (1.1)

в) Имеем согласно (1.3)

Задача 3.
Представить в алгебраической форме 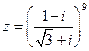
Решение:
Пусть 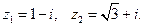 Имеем
Имеем 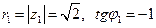 ; точка
; точка  принадлежит четвертому квадранту, поэтому
принадлежит четвертому квадранту, поэтому 
Date: 2015-07-02; view: 1198; Нарушение авторских прав