Тригонометрическая форма комплексного числа. Как говорилось выше, комплексное число удобно изображать точкой

Как говорилось выше, комплексное число удобно изображать точкой 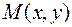. Можно также такое число отождествлять с радиус-вектором этой точки . При такой интерпретации сложение и вычитание комплексных чисел производится по правилам сложения и вычитания векторов. Для умножения и деления комплексных чисел более удобной оказывается другая форма.

Введём на комплексной плоскости 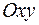полярную систему координат. Тогда 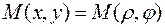, где 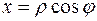, 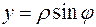и комплексное число можно записать в виде:

.

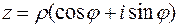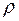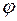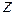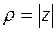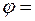
Эту форму записи называют тригонометрической (в отличие от алгебраической формы ). В этой форме число называют модулем, а – аргументом комплексного числа . Они обозначаются: , 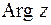. Для модуля имеем формулу

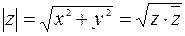
Аргумент числа определён неоднозначно, а с точностью до слагаемого 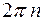, 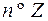. Значение аргумента, удовлетворяющего неравенствам 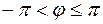, называется главным и обозначается 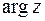. Тогда 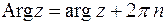, 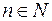. Для главного значения аргумента можно получить такие выражения:

,

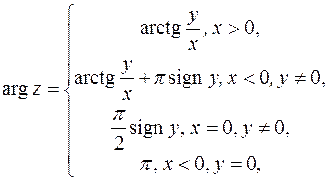аргумент числа 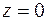считается неопределённым.

Условие равенства двух комплексных чисел в тригонометрической форме имеет вид: модули чисел равны, а аргументы отличаются на число кратное .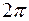

Найдём произведение двух комплексных чисел в тригонометрической форме:

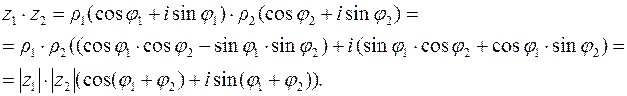
Итак, при умножении чисел их модули умножаются, а аргументы складываются.

Аналогичным образом можно установить, что при делении модули чисел делятся, а аргументы вычитаются.

Понимая возведение в степень как многократное умножение, можно получить формулу возведения комплексного числа в степень:

.

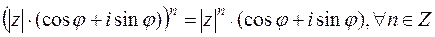Выведем формулу для 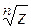– корня 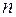-ой степени из комплексного числа 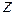(не путать с арифметическим корнем из действительного числа!). Операция извлечения корня является обратной по отношению к операции возведения в степень. Поэтому 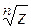– это комплексное число 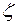такое, что .

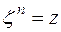Пусть 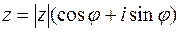известно, а 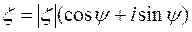требуется найти. Тогда

.

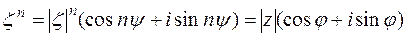Из равенства двух комплексных чисел в тригонометрической форме следует, что

, , .

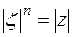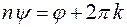Отсюда 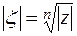(это арифметический корень!),

, .

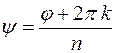Нетрудно убедиться, что 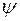может принимать лишь 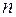различных по существу значений, например, при . Окончательно имеем формулу:

, .

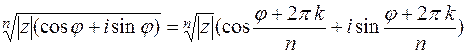Итак, корень 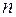-ой степени из комплексного числа имеет 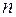различных значений. На комплексной плоскости эти значения располагаются в вершинах правильно 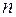-угольника, вписанного в окружность радиуса 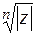с центром в начале координат. “Первый” корень имеет аргумент 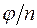, аргументы двух “соседних” корней отличаются на .

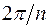Пример. Извлечём корень кубический из мнимой единицы: 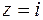, , 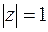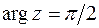. Тогда:

,

,

.

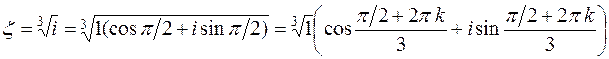
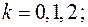
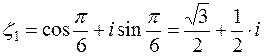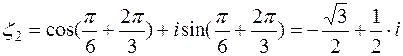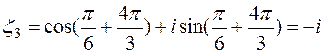Date: 2015-07-02; view: 853; Нарушение авторских прав