
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства комплексного сопряжения
|
|
1) 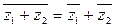
2) 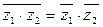 .
.
3) Если 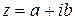 , то
, то 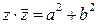 .
.
4) 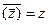 .
.
5) 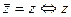 – вещественное число.
– вещественное число.
Доказательство проводится непосредственным вычислением.
Определение 3. Число 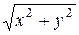 называется модулем комплексного числа
называется модулем комплексного числа 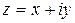 и обозначается
и обозначается 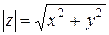 .
.
Очевидно, что 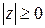 , причем
, причем 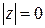
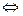
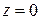 . Также очевидны формулы:
. Также очевидны формулы: 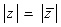 и
и 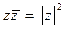 .
. 
2°. Свойства операций сложения и умножения.
1) Коммутативность: 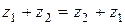 ,
, 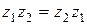 .
.
2) Ассоциативность: 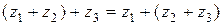 ,
, 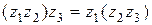 .
.
3) Дистрибутивность: 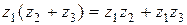 .
.
Доказательство 1) – 3) проводится непосредственными вычислениями на основе аналогичных свойств для вещественных чисел.
4) 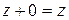 ,
, 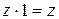 .
.
5) 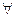
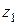 ,
, 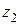
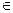 C
C 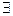 !
! 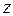 , удовлетворяющее уравнению
, удовлетворяющее уравнению 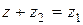 . Такое
. Такое
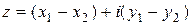 .
.
6) 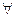
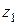 ,
, 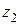
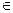 C,
C, 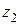
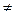 0,
0, 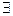 !
! 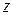 :
: 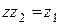 . Такое
. Такое 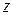 находится умножением уравнения на
находится умножением уравнения на 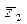
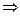

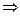
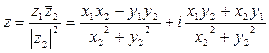 .
.
Пример. Представим комплексное число 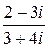 в алгебраической форме. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю. Имеем:
в алгебраической форме. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю. Имеем: 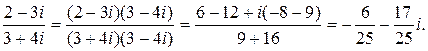
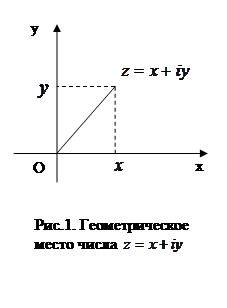 3°. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная форма записи комплексного числа.
3°. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная форма записи комплексного числа.
Пусть на плоскости задана прямоугольная система координат. Тогда 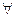
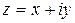
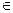 C можно поставить в соответствие точку на плоскости с координатами
C можно поставить в соответствие точку на плоскости с координатами 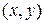 .(см. рис. 1). Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые − на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.
.(см. рис. 1). Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые − на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.
Отметим, что 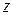 и
и 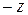 симметричны относительно начала координат, а
симметричны относительно начала координат, а 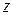 и
и 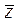 симметричны относительно Ox.
симметричны относительно Ox.
Каждому комплексному числу (т.е. каждой точке на плоскости) можно поставить в соответствие вектор с началом в точке O и концом в точке 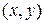 . Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу
. Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу 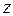 , обозначается той же буквой
, обозначается той же буквой 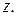
 Длина вектора
Длина вектора 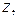 соответствующего комплексному числу
соответствующего комплексному числу 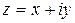 , равна
, равна 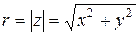 , причем
, причем 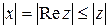 ,
, 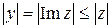 .
.
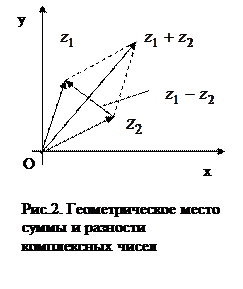
С помощью векторной интерпретации можно видеть, что вектор 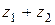 − сумма векторов
− сумма векторов 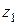 и
и 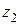 , а
, а 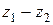 − сумма векторов
− сумма векторов 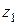 и
и 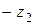 .(см. рис. 2). Поэтому справедливы неравенства:
.(см. рис. 2). Поэтому справедливы неравенства: 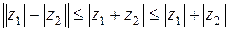 ,
,
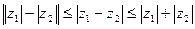 .
.
Наряду с длиной 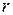 вектора
вектора 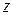 введем в рассмотрение угол
введем в рассмотрение угол 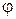 между вектором
между вектором 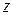 и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается
и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается 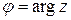 . Угол
. Угол 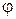 определяется не однозначно, а с точностью
определяется не однозначно, а с точностью 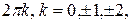 …. Для
…. Для 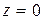 аргумент не определяется.
аргумент не определяется.
При этом
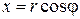 , , 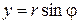 . .
| (5) |
Следовательно, любое комплексное число 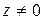 можно представить в виде
можно представить в виде
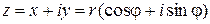 . .
| (6) |
Формулы (6) задают так называемую тригонометрическую форму записи комплексного числа.
Из (5) следует, что если 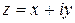 и
и 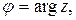 то
то
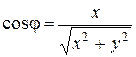 , , 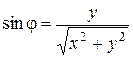 . .
| (7) |
Из (5) 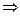 что по
что по 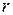 и
и 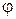 комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу
комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу 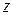 его модуль
его модуль 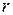 находится однозначно, а аргумент
находится однозначно, а аргумент 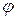 , в силу (7), − с точностью
, в силу (7), − с точностью 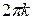 . Также из (7) следует, что аргумент
. Также из (7) следует, что аргумент 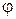 может быть найден как решение уравнения
может быть найден как решение уравнения
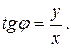
Однако не все решения этого уравнения являются решениями (7).
Среди всех значений аргумента комплексного числа выбирается одно, которое называется главным значением аргумента и обозначается 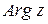 . Обычно главное значение аргумента выбирается либо в интервале
. Обычно главное значение аргумента выбирается либо в интервале 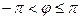 , либо в интервале
, либо в интервале 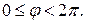
В тригонометрической форме удобно производить операции умножения и деления.
Теорема 1. Модуль произведения комплексных чисел 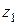 и
и 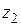 равен произведению модулей, а аргумент – сумме аргументов, т.е.
равен произведению модулей, а аргумент – сумме аргументов, т.е.
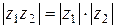 , а
, а 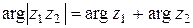 .
.
Аналогично
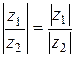 ,
, 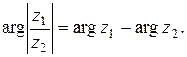
Доказательство. Пусть 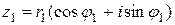 ,
, 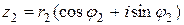 . Тогда непосредственным умножением получаем:
. Тогда непосредственным умножением получаем:
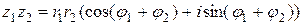 .
.
Аналогично
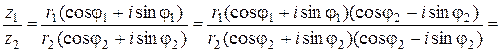
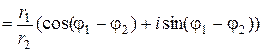 .■
.■
Следствие (формула Муавра). Для 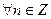 справедлива формула Муавра
справедлива формула Муавра
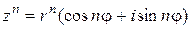 .
.

|
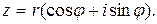 Найдем геометрическое местоположение точки
Найдем геометрическое местоположение точки 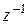 . Из теоремы 1 следует, что
. Из теоремы 1 следует, что 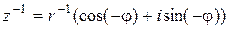 .
.
Поэтому для ее построение необходимо вначале построить точку 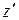 , являющуюся инверсией
, являющуюся инверсией 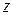 относительно единичной окружности, а затем найти точку, симметричную ей относительно оси Ox.
относительно единичной окружности, а затем найти точку, симметричную ей относительно оси Ox.
Пусть 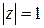 , т.е.
, т.е. 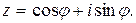 Комплексное число
Комплексное число  обозначается
обозначается 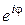 , т.е.
, т.е. 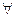
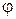
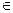 R справедлива формула Эйлера
R справедлива формула Эйлера
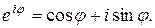
| (8) |
Так как  , то
, то 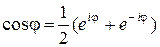 ,
, 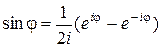 . Из теоремы 1
. Из теоремы 1 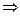 что с функцией
что с функцией 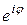 можно работать как с обычной показательной функцией, т.е. справедливы равенства
можно работать как с обычной показательной функцией, т.е. справедливы равенства
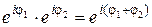 ,
, 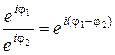 ,
, 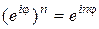 .
.
Из (8) 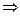 показательная форма записи комплексного числа
показательная форма записи комплексного числа
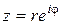 , где
, где  ,
, 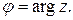
Пример. 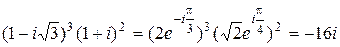 .
.
4°. Корни 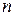 -ой степени из комплексного числа.
-ой степени из комплексного числа.
Рассмотрим уравнение
 , , 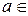 С, С, 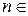 N. N.
| (9) |
Пусть 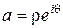 , а решение уравнения (9) ищется в виде
, а решение уравнения (9) ищется в виде 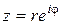 . Тогда (9) принимает вид
. Тогда (9) принимает вид 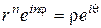 , откуда находим, что
, откуда находим, что 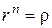 ,
, 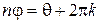 , т.е.
, т.е.
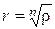 ,
, 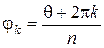 ,
, 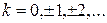 .
.
Таким образом, уравнение (9) имеет корни
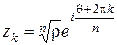 , , 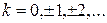 . .
| (10) |
Покажем, что среди (10) имеется ровно 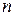 различных корней. Действительно,
различных корней. Действительно, 
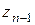 различны, т.к. их аргументы
различны, т.к. их аргументы 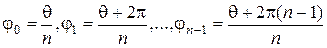 различны и отличаются меньше, чем на
различны и отличаются меньше, чем на 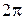 . Далее,
. Далее, 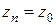 , т.к.
, т.к. 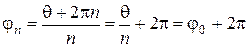 . Аналогично
. Аналогично 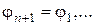 .
.
Таким образом, уравнение (9) при 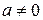 имеет ровно
имеет ровно 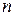 корней
корней 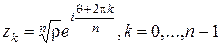 , расположенных в вершинах правильного
, расположенных в вершинах правильного 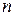 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса  с центром в т. O.
с центром в т. O.
Таким образом, доказана
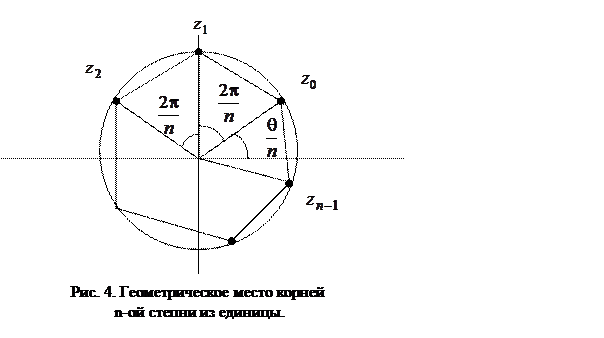
Теорема 2. Извлечение корня 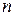 -ой степени из комплексного числа
-ой степени из комплексного числа 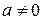 всегда возможно. Все значения корня
всегда возможно. Все значения корня 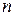 -ой степени из
-ой степени из 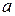 расположены в вершинах правильного
расположены в вершинах правильного 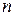 -угольника, вписанного в окружность с центром в нуле и радиуса
-угольника, вписанного в окружность с центром в нуле и радиуса 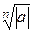 . При этом,
. При этом,
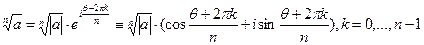 .
.
Следствие. Корни 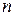 –ой степени из 1 выражаются формулой
–ой степени из 1 выражаются формулой
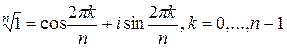 .
.
Произведение двух корней из 1 является корнем, 1 – корень 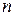 -ой степени из единицы,
-ой степени из единицы, 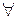 корня
корня 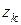
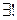
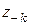 :
: 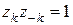 .
.
Date: 2015-07-02; view: 910; Нарушение авторских прав