Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
III. Действия с комплексными числами в алгебраической форме
|
|
Сложение комплексных чисел. Суммой двух комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = (a+c) + (b+d)i.
Произведение комплексных чисел
Перемножим комплексные числа z1= a + bi и z2 = c + di по правилам умножения многочленов: z1∙z2 = (a + bi)(c + di) = ac + bci + adi + bdi2 = (ac - bd) + (ad + bc)i.
Деление комплексных чисел.
Для выполнения деления комплексных чисел выполняют последовательно три операции:
1. Частное комплексных чисел записывают в виде дроби.
2. Числитель и знаменатель дроби домножают на число комплексно-сопряжённое со знаменателем.
3. Числитель полученной дроби почленно делят на знаменатель.
Примеры:
1. Произведение комплексных чисел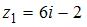 
и 
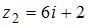равно …
Решение:
Произведение данных комплексных чисел можно найти по правилу умножения двучленов или используя формулу разности квадратов 
С учетом равенства 
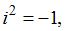получим:
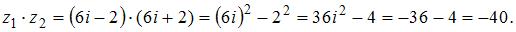
Ответ: -40
Решите самостоятельно:
1. Произведение комплексных чисел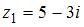 
и 
равно …
1. Произведение комплексных чисел 
и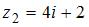 
равно …
-20
2. Произведение комплексных чисел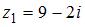 
и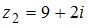 
равно …
Date: 2015-07-02; view: 683; Нарушение авторских прав