Комплексные числа

Заметим, что простейшее квадратное уравнение

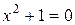(6)

не имеет решения в множестве действительных чисел. Это так, поскольку квадрат любого действительного числа не может быть числом отрицательным и в сумме с положительным числом 1 дает число >0, большее нуля. Но уравнение (6) можно обратить в тождество, если считать числом – «мнимой единицей», которое обозначают буквой 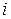. Основное его свойство:

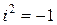. (7)

Тогда решением для аналогичного уравнения 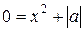будет 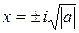. В итоге проверки имеем: .

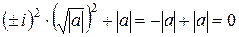Определение: модуль любого действительного числа 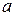имеет неотрицательное значение:

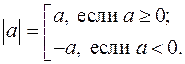. (8)

Известно, что квадратное уравнение

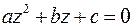, (9)

где 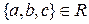, имеет действительное решение, 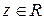, когда его дискриминант 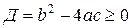. Применение для 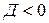мнимой единицы, имеющей свойство (7), позволяет записать 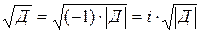и получить численное решение для уравнения (9) в виде 2^х комплексных чисел:

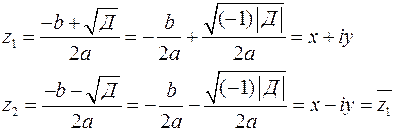; (10)

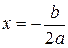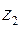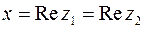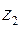Здесь – действительная часть комплексных чисел и . Это записывают: . В (10) – мнимая часть комплексного числа и 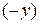– мнимая часть комплексного числа 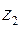. Это записывают: 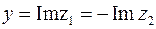. Числа и 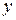вещественные, 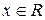и .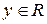

В (10) комплексные числа и 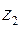взаимно сопряженные. Комплексное сопряжение обозначают «*» справа вверху от числа или чертой над ним

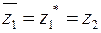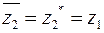, . (11)

Операция комплексного сопряжения меняет только знак мнимой части комплексного числа z на противоположный знак (см. равенство (10)).

Каждую формулу (10) надо читать как единую запись одного комплексного числа в координатной форме

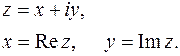. (12)

Комплексное число 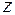, у которого 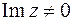, называют существенно комплексным числом.

Модулем комплексного числа (12) называют неотрицательное значение

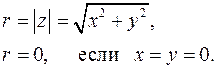(13)

Каждому комплексному числу, записанному в форме (12), соответствует упорядоченная пара вещественных чисел: . Их можно рассматривать, как координаты точки на ортогональной декартовой плоскости 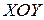. Эту же упорядоченную пару чисел можно рассматривать как декартовые координаты вектора , проведенного из начала ортогональной системы в точку 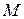. Наоборот каждой точке и, соответственно, вектору ставится в соответствие комплексное число 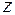(равенство (12)). Тогда горизонтальную ось «комплексной плоскости» обозначают 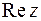, а мнимую ось 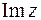. Угол , который радиус-вектор образует с положительной осью 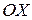, называют аргументом комплексного числа 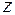и обозначают . Поворот радиус вектора на угол дает то же значение (12) комплексного числа. Поэтому значение определяется комплексным числом 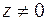с точностью до целочисленного значения , 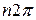. Если значение аргумента комплексного числа такое, что , его обозначают . 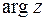Ясно, что

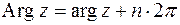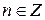, (14)

Поскольку период функции 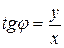равен 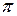, то применение обратной тригонометрической функции 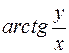для определения 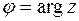ограниченно следующим правилом:

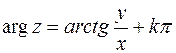, (15)

где 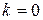для точки 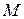в 1^ой и 4^ой четвертях, 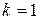, когда точка находится во второй четверти, и , когда точка находится в 3^ей четверти.

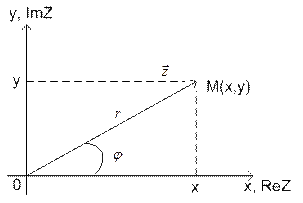
Рисунок 1.

Для прямоугольного треугольника (см. Рис. 1) можно записать очевидные тождества, связанные с определением тригонометрических функций 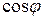и .

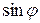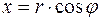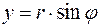, (16)

Тогда можно записать эквивалентное (12) выражение:

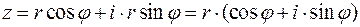. (17)

Выражение (17) называют тригонометрической записью комплексного числа. Замена в (17) на 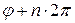, , 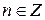в силу периодичности тригонометрических функций не изменяет значение .

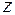Два комплексных числа равны, если, соответственно, равны их действительные и мнимые части.

После применения в (17) формулы Эйлера

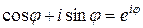, (18)

перейдем к экспоненциальной, показательной, записи комплексного числа

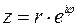. (19)

Формула (18) доказывается в теории рядов посредством установления равенства рядов, представляющих левую и правую части этого тождества. (Ряды изучаются в третьем семестре).

Связь между комплексными числами и векторами на плоскости, то есть с их проекциями на оси координат, становится полной после определения операции сложения комплексных чисел и :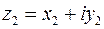

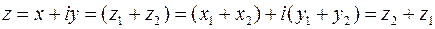. (20)

Разность комплексных чисел определяется как операция обратная сложению: 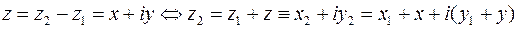, где знак «» обозначает «равносильность» равенств. Отсюда 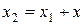и 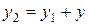. Тогда соответственно имеем

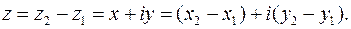(21)

Равенства (20) и (21) полностью совпадают с равенствами для проекций суммы и разности двух векторов, что иллюстрируют рисунки 2 и 3.

Рисунок 2.

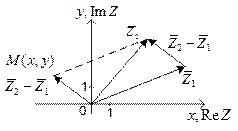
Рисунок 3.

На рисунке 3 в точку 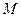направлен вектор 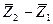, который однозначно соответствует разности комплексных чисел 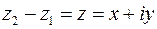, определяемой по формуле (21).

Это соответствие между комплексными числами и векторами на плоскости, с точностью до их сложения и вычитания, называют изоморфизмом.

Изоморфизм комплексных чисел и векторов на плоскости используется, например, в электротехнике. Для расчета сложных электрических цепей с равным успехом применяют и «метод векторных диаграмм», и «метод комплексных амплитуд». Результаты, естественно, совпадают.

Произведение двух комплексных чисел определяется как алгебраическая операция умножения двучлена 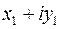на двучлен 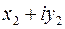. При этом учитывается 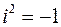и проводится приведение подобных величин, не содержащих и содержащих множителем мнимую единицу ,

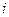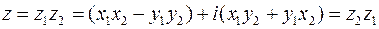. (22)

Для тригонометрической или показательной записи комплексного числа, 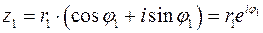, 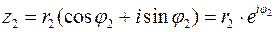и 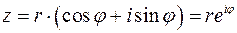получение произведения (22) упрощается:

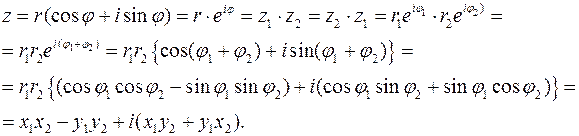(23)

Модуль числа 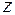равен произведению модулей перемножаемых комплексных чисел и его аргумент равен сумме аргументов этих чисел.

По этому правилу умножения комплексных чисел, (23), можем записать 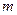-ую степень комплексного числа 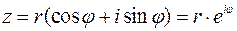в тригонометрической и экспоненциальной записи:

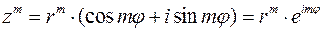(24)

При 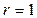получаем известную формулу Муавра:

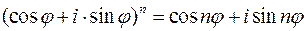. (24′)

Она верна при любых целых показателях .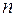

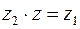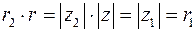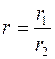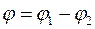Операция деления для комплексных чисел определяется, как операция обратная операции умножения комплексных чисел. То есть равенство равносильно равенству . Тогда верно: и . Отсюда следует: , и соответственно получим:

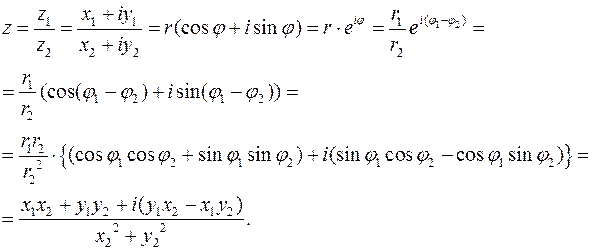(25)

Координатная запись в (25) результата деления комплексных чисел и в (23) результата их умножения получена применением равенств: , , 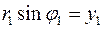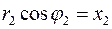и .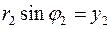

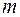Для операции возведения в степень обратной операцией будет, как отмечалось выше, операция извлечения корня. Для комплексного числа извлечение корня любой степени не является однозначной операцией. Действительно, число является корнем -ой степени из числа 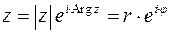, если 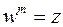. Тогда верно:

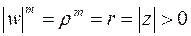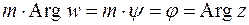, . (26)

Вследствие неоднозначност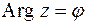и и 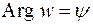(см (14)) в общем случае равенство нужно рассматривать как равенство двух множеств:

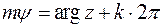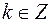, (27)

При решении уравнений (26) необходимо учитывать равенство (27), полагая в нем 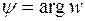. В результате получим одно значение модуля

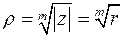(26′)

и 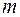различных значений аргумента корня, интервал изменения которого не превышает 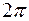, при этом 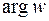получает индекс:

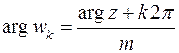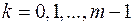, , где 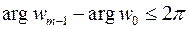. (27′)

Получили 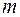различных значений корня

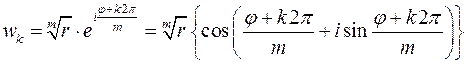, (28)

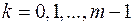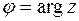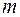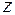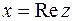где , , . При этом возведение каждого корня (28) в -ую степень дает . Соединяя начало координат плоскости , где и 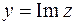, с точками 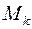, изображающими комплексные числа (см. (28)), получим 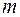-конечную звезду, см., например см. Рис. 4, поскольку у всех одинаковые значения модуля .

Пример 1. Для комплексного числа 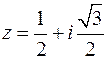найти модуль, аргумент и записать его в тригонометрическом и экспоненциальном виде. Определить все корни 5^ой степени из этого комплексного числа.

Решение.

Модуль числа равен:

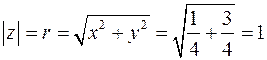
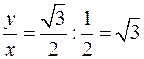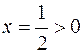Так как и , и 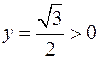, то точка 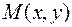лежит в первой четверти. Поэтому в формуле (15) :

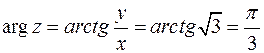
В итоге:

.

Вычислим модуль для корня 5-ой степени из числа 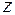по формуле (26′)

.

По (27′) мы получим пять различных значений аргумента, разность между которыми не превышает ,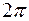

, .

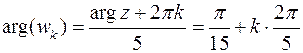Для 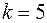получим и, соответственно, повторим значение корня: 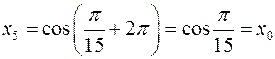; . То есть различными будут только 5 значений:

,

,

,

,

.

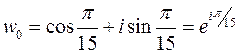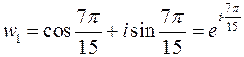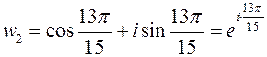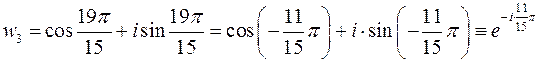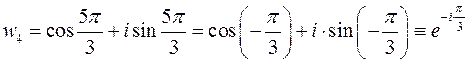Для полученных корней значения 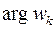приведены к стандартному интервалу: , . Точки 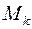комплексной плоскости, ответствующие комплексным числам , делят окружность радиуса 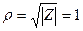с центром в начале координат на пять равных дуг (см. Рис. 4).

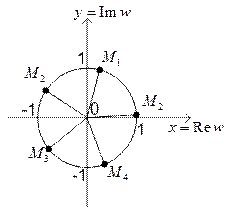
Рисунок 4.

Задача решена.

Операция комплексного сопряжения связана с заменой 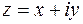на . Такой операции на Рис. 5 отвечает отражение вектора 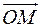относительно оси 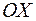. После отражения он совпадает с вектором .

Комплексное сопряжение над результатом каждого арифметического действия равносильно замене всех комплексных чисел, с которыми производится арифметическое действие, на комплексно сопряженные числа. Для операции сложения соответствующее отражение всех векторов относительно оси 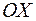проиллюстрировано на рисунке 5. Отражение соответствующих сторон параллелограмма относительно оси приводит к отражению относительно этой оси всего параллелограмма.

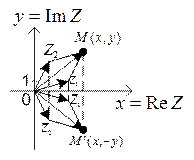
Рисунок 5.

Ниже приведены все тождества для арифметических операций, связанные с комплексным сопряжением:

1) ,

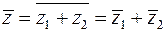2) ,

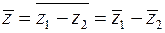3) ,

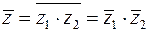4) 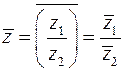, (29)

5) ,

6) ,

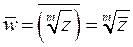7) .

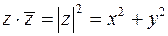Тождество 1) и аналогично тождество 2) легко доказать геометрически, что проиллюстрировано на рисунке 5.

Тождества 3), 4), 5) и 6), 7) легко доказываются с помощью тригонометрической записи комплексного числа. Например,

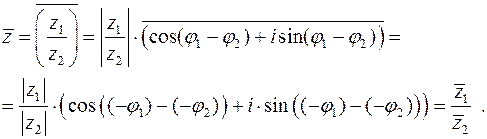
Другие функции комплексного аргумента будут рассмотрены позже.

Замечание: При выполнении операций сложения и вычитания удобнее применять координатную запись комплексного числа, 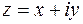, а при умножении, делении, возведении в степень или при извлечении корня из комплексного числа удобнее применять тригонометрическую или показательную запись комплексного числа, .

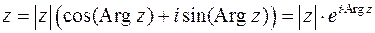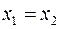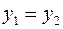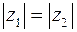Равенство комплексных чисел, как и векторов, предполагает равенство их координат: и , если . Им равносильны равенства: и 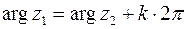, 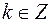. Аналогично, изоморфные комплексным числам вектора равны, если равны их длины и направления.

Замечание: Из изоморфизма комплексных чисел и векторов на плоскости следует, что комплексные числа можно сравнивать только по модулю. То есть можно проверить выполнение неравенства 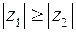или 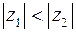, но неравенства 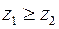и 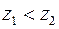не имеют смысла. Это нужно учитывать при решении уравнений или неравенств, содержащих комплексные числа.

Пример 2. Вычислить: 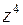, если .

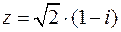Решение:

Для 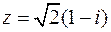имеем 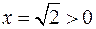, , 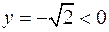число 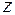принадлежит четвертой четверти комплексной плоскости и в формуле (15) :

.

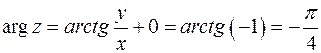Согласно (13) (по определению):

.

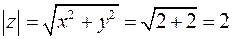Запишем 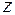в показательной или тригонометрической форме:

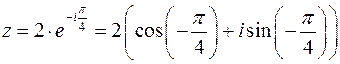
Тогда согласно (24):

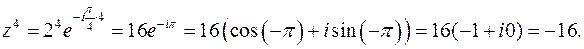
Задача решена.

Пример 3. Решить уравнение: .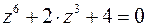

Решение:

Пусть , тогда квадратное уравнение 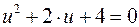имеет дискриминант .

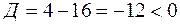Поэтому получим два комплексно сопряженных решения:

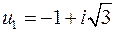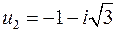; , где .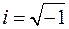

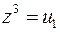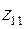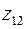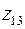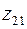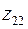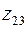Учитывая обозначение и формулу (28) для корня комплексного числа получим три значения , и для кубического корня из и три значения , , для кубического корня из .

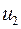Для : 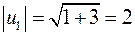, 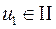-ой четверти и в формуле (13) 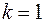. Поэтому .

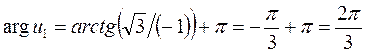По формулам (28) получаем:

,

,

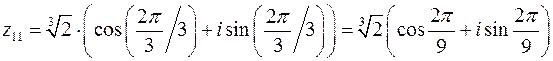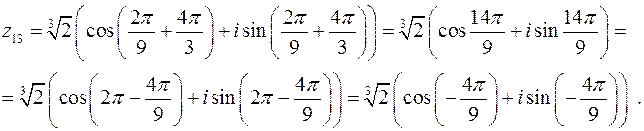Здесь учтено стандартное ограничение на допустимые значения :

.

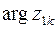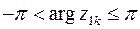Решая аналогичное уравнение 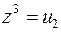, получаем что 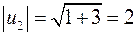, 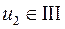-ей четверти, в (13) 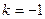и .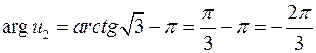

В этом случае из формул (28) следует:

,

,

.

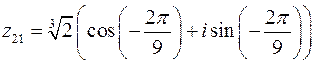Всем решениям уравнения отвечают точки, лежащие на круге радиуса с центром в начале координат комплексной плоскости (см. Рис. 6).

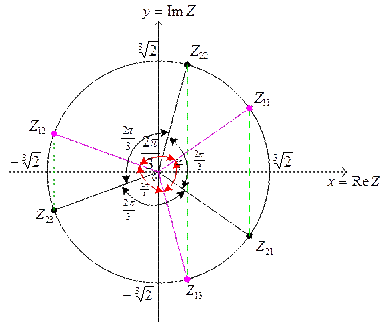
Рисунок 6.

Задача решена.

Пример 4. Решить неравенство: .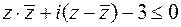

Решение:

Учитывая, что согласно (10) 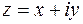и , получим неравенство 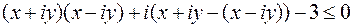, которое не содержит мнимой единицы и превращается в неравенство только для вещественных координат точек плоскости, которое ограничивает их допустимые значения:

.

Выделяя полные квадраты, получим эквивалентное неравенство

. (*)

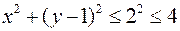В случае равенства в (*) из него получаем уравнение окружности

(**)

радиуса 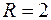с координатами её центра: 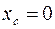, 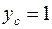. Отсюда следует, что неравенству (*) удовлетворяют все точки круга, ограниченного окружностью (**), включая его границу (см. Рис. 7).

Рисунок 7.

Задача решена.

Date: 2015-07-02; view: 982; Нарушение авторских прав