Числа натуральные, целые, рациональные и иррациональные

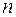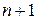Знакомство с количественными соотношениями начинается с прямого счета: 1, 2, 3, 4, 5, …. Им пользуются при определении количества однородных предметов: тетрадей, книг, CD дисков и т. д. Результат достигается сложением положительных целых чисел. Например, следующее за числом число получается прибавлением единицы к 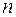. Все такие числа образуют множество натуральных чисел, которое обозначается заглавной буквой 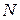латинского алфавита:

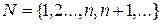(1)

В фигурных скобках указаны элементы этого множества.

Определение–пояснение: множеством называют совокупность однородных элементов, объединенных общим свойством или признаком.

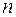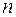Обратный счет встречается при решении задач связанных с вычитанием из одного натурального числа второго. Например, вычитая из числа единицу, получим число . Вычитая единицу раз, подряд, из числа 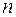, получим число «0», обозначающее отсутствие перечисляемых предметов, их количество равно нулю. Дальнейшее вычитание приводит к отрицательным числам: 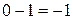, 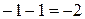≡ 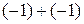и т. д. Вычитание обратно сложению. 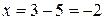Так равенству отвечает число , получаемое вычитанием большего числа 5 из меньшего числа 3. Натуральные числа, число «0» и отрицательные целые числа образуют множество целых чисел. Это множество обозначают заглавной буквой 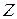латинского алфавита:

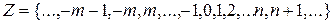(2)

Арифметическая операция умножения является сокращенной записью сложения одинаковых чисел. Так запись 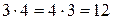обозначает равные количества, получаемые сложением четырех чисел 3 или трех чисел 4: .

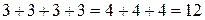Деление появляется, как обратная операция для умножения. Так, уравнение 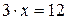обращается в тождество для значения 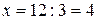. Не всегда уравнение 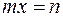имеет решением целочисленное значение 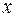, есл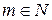и и 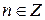. Когда 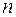не делится без остатка на 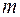, получаем нецелое число

(3)

“Довиетовские” алгебраисты ограничивались заявлением, что «такое деление не возможно». Сейчас это рациональные числа.

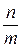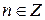Несократимые (положительные и отрицательные) дроби , где и 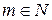, образуют множество рациональных чисел, которое обозначают заглавной буквой 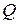латинского алфавита, .

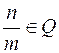Степень числа – это сокращенная запись умножения нескольких одинаковых чисел. Так, при определении, например, общей длины приставленных друг к другу трех одинаковых стержней, по 3 см каждый, мы получим 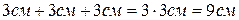. Для математики не существенны единицы измерения складываемых однородных величин, то есть величин одинаковой размерности. Важны только количественные соотношения. Тогда в нашем случае 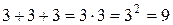, говорят: «три в степени 2 равно 9». В общем случае произведение 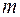одинаковых чисел 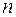записывают сокращенно, как 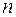в степени 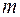, то есть .

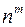Для операции возведения в степень обратной будет операция извлечения корня. Так, если 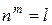, то 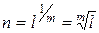, говорят: «корень 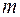-ой степени из числа ». С помощью обратной операции решается уравнение 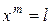. Замечание: когда 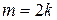– четное число, тогда 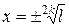, так как .

В отличие от уравнения 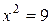с решениями 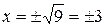, для которых 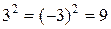, решениями уравнения 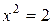являются числа 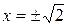, которые уже не принадлежат ни множеству целых, ни множеству рациональных чисел, 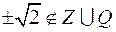. Знак «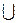» обозначает объединение множеств. Такие числа, как 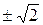, , 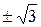число «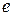», число «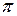» и др., которые представляются бесконечной непериодической дробью, называют иррациональными числами и обозначают заглавной буквой 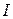латинского алфавита.

Иррациональные числа появляются тогда, когда, например, два отрезка «несоизмеримы», то есть, когда нельзя найти отрезок конечной длины, укладывающийся целое число раз в каждом из измеряемых отрезков. Иррациональность числа 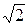связана с несоизмеримостью катета равнобедренного прямоугольного треугольника с его гипотенузой; - иррациональное число, так как ребро куба несоизмеримо с его объемной диагональю; 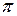- иррациональное число вследствие несоизмеримости длины окружности с ее диаметром; число 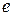иррациональное число, так как по определению оно равно бесконечной сумме убывающих рациональных чисел:

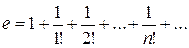, (4)

где 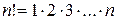., читают «эн факториал равен произведению всех натуральных чисел от 1 до ».

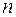Числа целые, рациональные и иррациональные образуют множество действительных чисел, которое обозначают заглавной буквой 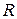латинского алфавита:

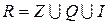. (5)

Важно, что действительные числа «сплошь» заполняют числовую ось. То есть между любыми двумя сколь угодно близкими числами 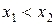можно вставить бесконечное число действительных чисел. Это свойство действительных чисел играет «главную» роль в теории пределов, изучаемой в этом семестре. Но при вычислении на ЭВМ это свойство действительных чисел нарушается. Машинное представление числа с конечной мантиссой и порядком всегда содержит только конечное число чисел. Это может привести к ошибочному результату при решении нелинейных уравнений или систем уравнений. Об этом, по крайней мере, нужно знать и по возможности проверять полученное решение на «здравый смысл», в определенных частных случаях проверять его совпадение с имеющимся очевидным результатом.

Стоит заметить, что расширение числового «множества» от натуральных чисел до действительных чисел не является произвольным. Следует ожидать усложнения множества чисел по мере включения в рассмотрение новых уравнений, например, степенных, показательных и т. д. Но усложнение не является произвольным. Имеется «в природе» некий механизм расширения числового множества (числового поля). Фундаментальная идея, дающая такую общую схему, сформулирована немецким математиком Германом Хенкелем в 1867 г. Ранее ее элементы рассматривал Уильям Гамильтон. Её называют «принципом перманентности». Согласно этой схеме:

1) Среди элементов расширенного числового множества содержится последовательность натуральных чисел.

2) Есть критерий, устанавливающий равенство или неравенство всех элементов числового множества. В случае, когда элементы являются натуральными числами, этот критерий превращается в известное правило сравнения натуральных чисел.

3) Для любых двух элементов множества задается схема сложения и умножения, подчиняющаяся перестановочному, сочетательному и распределительному законам. Она превращается в схему действия над натуральными числами, когда числа являются таковыми.

Date: 2015-07-02; view: 1187; Нарушение авторских прав