
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

и многочлены
|
|
Комплексные числа
Методические указания
к решению задач
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
УДК 512.64(07)
Комплексные числа и многочлены: Методические указания к решению задач / Сост.: М. Н. Абрамова, Е. А. Толкачева, А. И. Куприянов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007. 32 с.
Содержат примеры решения основных типов задач высшей алгебры. Разобраны различные методы решения этих задач.
Предназначены для студентов-заочников всех специальностей.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2007
При изучении курса высшей математики, включающего наряду с другими разделами комплексные числа и многочлены, делается упор на умение студента самостоятельно решать задачи с использованием различных методов. В связи с этим настоящее издание призвано помочь студентам-заочникам младших курсов в их самостоятельной работе.
Несмотря на то, что студент может использовать любые источники, содержащие сведения по высшей алгебре, в данных указаниях в качестве основного выбран один из них – «Конспект лекций по высшей математике» Д.Т. Письменного [1] – издание, наиболее доступное, с точки зрения составителей. Поэтому в начале каждой темы дается ссылка на конкретные страницы названного учебного пособия.
Решение каждого примера в предлагаемых указаниях заканчивается ответом, который или подчеркнут, или записан отдельно.
1. КОМПЛЕКСНЫЕ ЧИСЛА
1.1. Определение комплексных чисел и действия над ними
1.1.1. Сложение и умножение комплексных чисел в алгебраической форме
Определение комплексных чисел приведено в [1, с. 186-187]. Для решения многих задач важна алгебраическая форма записи комплексного числа z = x + yi, где x, y 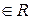 ;
;
x = Re z – действительная часть числа z;
y = Im z – мнимая часть числа z.
В дальнейшем по умолчанию под x и y будем понимать именно действительную и мнимую части комплексного числа z.
Число i – мнимая единица. Для нее верно равенство: 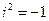 , а также верно, что
, а также верно, что 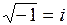 и
и 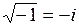 .
.
Исходя из этого, определим на примерах результат возведения i в различные степени:
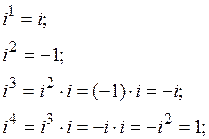
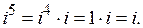
Обобщим результат и получим формулу для нахождения 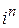 :
:
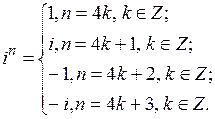
Действия над комплексными числами в алгебраической форме производятся по правилам действия над многочленами относительно величины i, при этом важно помнить, что 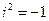 [1, с. 188-189].
[1, с. 188-189].
Пример 1. Выполнить действия: (5+3 i)+ (–2– i)= 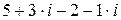 =
=
= (5–2)+ (3–1) i = 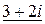
Пример 2. Выполнить действия:2×(3+4 i)+ (5–3 i) (1+2 i). Раскрываем скобки, пользуясь правилами действий над многочленами: 2×3 + 2×4 i + 5×1 +
+ 5×2 i – 3 i ×1 – 3 i ×2 i = [учитываем, что i × i = 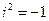 ] = 6 + 8 i + 5 + 10 i –3 i + 6 =
] = 6 + 8 i + 5 + 10 i –3 i + 6 =
= 6 + 5 + 6 + (8 + 10 – 3) i = 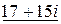 .
.
Пример 3. Найти вещественные x и y из равенства
(1 + 2 i) x + (3 – 5 i) y = 1 – 3 i.
Решение. Раскрываем скобки, пользуясь правилами действий над многочленами:
x + 2 ix + 3 y – 5 iy = 1 – 3 i.
Группируем вещественные и мнимые части равенства
(x + 3 y) + (2 x – 5 y) i = 1 – 3 i.
Используя определения равенства комплексных чисел, приравниваем вещественные и мнимые части левой и правой частей равенства:
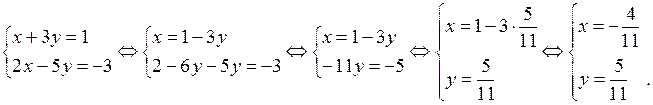 Ответ:
Ответ: 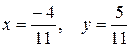 .
.
1.1.2. Деление комплексных чисел в алгебраической форме
Определение:
Комплексное число 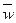 = x – yi называется сопряженным числом по отношению к w = x + yi.
= x – yi называется сопряженным числом по отношению к w = x + yi.
Примеры сопряженных комплексных чисел:
–1 + 5 i и –1 – 5 i, 2 – 3 i и 2 + 3 i.
Для деления двух комплексных чисел в алгебраической форме, как правило, удобно числитель и знаменатель дроби домножать на число, сопряженное знаменателю [1, с. 190-191].
Пример 4. Выполнить деление: 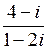 = [домножаем числитель и знаменатель дроби на число, сопряженное знаменателю] =
= [домножаем числитель и знаменатель дроби на число, сопряженное знаменателю] =
= 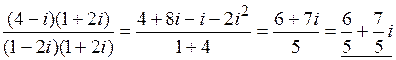 . Заметим, что
. Заметим, что 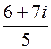 есть выражение, а не число, поэтому его нельзя рассматривать как ответ.
есть выражение, а не число, поэтому его нельзя рассматривать как ответ.
Пример 5. Выполнить действия:  =
=
= 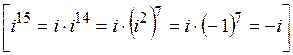
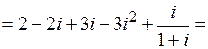
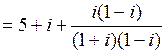 =
= 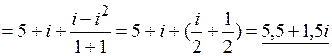 .
.
Пример 6. Выполнить действия: 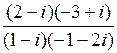 = [домножаем числитель и знаменатель дроби на числа, сопряженные обоим числам знаменателя] =
= [домножаем числитель и знаменатель дроби на числа, сопряженные обоим числам знаменателя] =
= 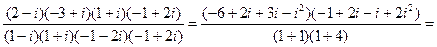
= 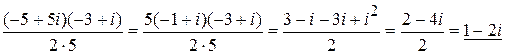 .
.
1.1.3. Извлечение квадратного корня из комплексного числа в алгебраической форме
Определение. Комплексное число 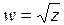 называется квадратным корнем из комплексного числа z, если
называется квадратным корнем из комплексного числа z, если 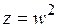 [1, с. 191].
[1, с. 191].
Пример 7. Вычислить 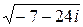 .
.
Решение. Пусть 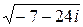 = x + yi, тогда
= x + yi, тогда
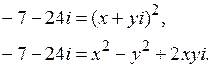
Составляем систему, приравнивая вещественные и мнимые части левой и правой частей равенства:
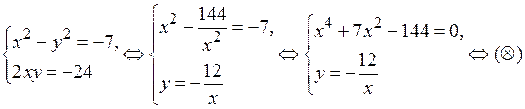
Решим отдельно биквадратное уравнение:
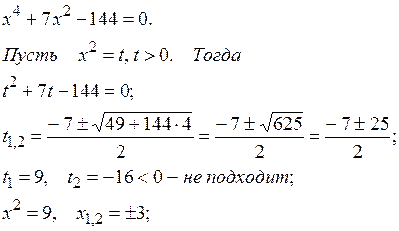
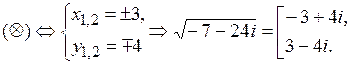
Ответ: {‑3 + 4 i; 3 ‑ 4 i }.
Другой способ решения возможен после введения тригонометрической формы записи комплексного числа (см. с. 14).
1.2. Решение линейных и квадратных уравнений для комплексных чисел
В области комплексных чисел верны те же формулы для решения линейных и квадратных уравнений, что и в области действительных чисел.
Пример 8. Решить уравнение: (‑2 ‑ i) z = 3 + i.
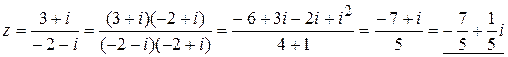
Пример 9. Решить уравнение: 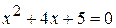 .
.
Решение. Воспользуемся формулой для нахождения корней квадратного уравнения:
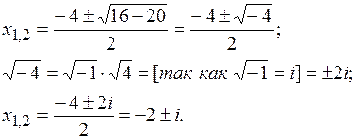
Ответ: {‑2 + i; ‑2 – i }.
Пример 10. Решить уравнение: 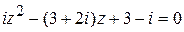 .
.
Решение:
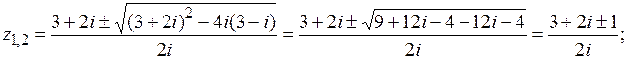
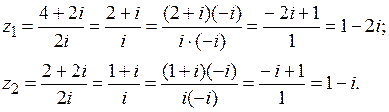
Ответ: {1 ‑ 2 i; 1 – i }.
Пример 11. Решить уравнение: 
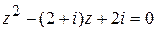 .
.
Решение:
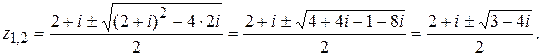
Вычислим 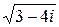 :
:
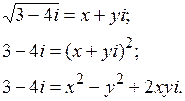
Составляем систему, приравнивая вещественные и мнимые части левой и правой частей равенства:
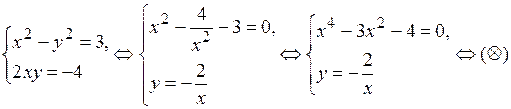
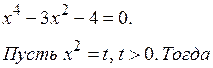
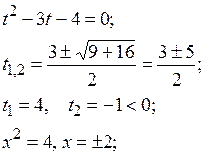
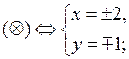
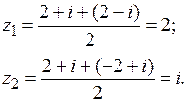
Ответ: {2; i }.
Пример 12. Решить систему уравнений:
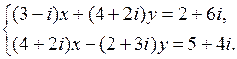
Решение. Выражаем из первого уравнения системы переменную x через переменную y:
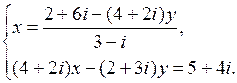
Домножаем числитель и знаменатель дроби на число, сопряженное знаменателю:
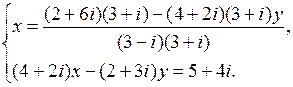
В числителе дроби раскрываем скобки и приводим подобные слагаемые:
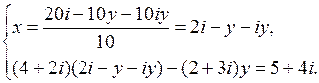
Подставляем полученное значение переменной x во второе уравнение системы:
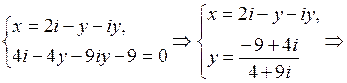
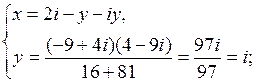 ;
;
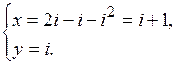
Ответ: {1 + i; i }.
1.3. Тригонометрическая форма записи комплексных чисел
3.1.4. Геометрическое изображение комплексных чисел
При изучении свойств комплексных чисел весьма удобной является их геометрическая интерпретация [1, с. 186-187]. Поскольку комплексное число определяется как пара действительных чисел, то каждое комплексное число z = a + bi изображается точкой плоскости (x, y) с координатами x = a и y = b. Такая плоскость называется комплексной плоскостью, ось абсцисс ‑ действительной (Re z), а ось ординат ‑ мнимой осью (Im z).
Пример 13. Изобразить на плоскости точки, соответствующие числам: 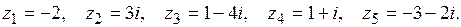
 Решение. У числа z 1 действительная часть равна ‑2, а мнимая ‑ 0. Следовательно, изображением числа z 1 служит точка (‑2, 0) (рис. 1.1).
Решение. У числа z 1 действительная часть равна ‑2, а мнимая ‑ 0. Следовательно, изображением числа z 1 служит точка (‑2, 0) (рис. 1.1).
У числа z 2 действительная часть равна 0, а мнимая равна 3. Следовательно, изображением числа z 2 служит точка (0, 3). У числа z 3 действительная часть равна 1, а мнимая ‑4. Следовательно, изображением числа z 3 служит точка (1, ‑4).
У числа z 4 действительная часть равна 1 и мнимая 1. Следовательно, изображением числа z 4 служит точка (1, 1).
У числа z 5 действительная часть равна ‑3, а мнимая ‑2. Следовательно, изображением числа z 5 служит точка (‑3, ‑2).
Сопряженные числа изображаются точками на комплексной плоскости, симметричными относительно действительной оси Re z.
3.1.5. Тригонометрическая форма записи комплексных чисел
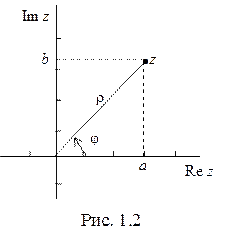 Рассмотрим другую важную форму представления комплексных чисел [1, с. 187-188]:
Рассмотрим другую важную форму представления комплексных чисел [1, с. 187-188]: 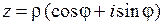 , где
, где 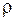 – модуль комплексного числа, а
– модуль комплексного числа, а 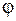 – его аргумент.
– его аргумент.
Связь между алгебраической и тригонометрической формами записи можно получить из равенства: 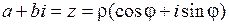 . Тогда
. Тогда 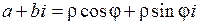 , откуда
, откуда
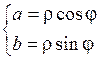 . Возведя оба равенства в квадрат и сложив их, получим
. Возведя оба равенства в квадрат и сложив их, получим 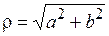 . А угол
. А угол 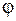 определяется с точностью до
определяется с точностью до 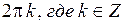 , из системы:
, из системы:
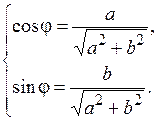 (1.1)
(1.1)
Для однозначного соответствия между комплексным числом и его аргументом выделим его главное значение arg z, для которого принимаем: 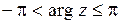 . В дальнейшем будем придерживаться ограничений:
. В дальнейшем будем придерживаться ограничений: 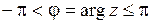 . Для числа z = 0 аргумент не определяется.
. Для числа z = 0 аргумент не определяется.
Геометрический смысл 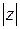 и arg z ясен из рис 1.2:
и arg z ясен из рис 1.2: 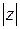 есть расстояние от точки до начала координат, а arg z – угол, на который необходимо повернуть вещественную ось Re z до совпадения с числом z.
есть расстояние от точки до начала координат, а arg z – угол, на который необходимо повернуть вещественную ось Re z до совпадения с числом z.
Пример 14. Представить в тригонометрической форме число z = 1.
Для числа z = 1 a = 1, b = 0. Следовательно, 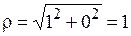 и по формуле (1.1) находим
и по формуле (1.1) находим  Эта система имеет решение:
Эта система имеет решение: 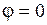 . В итоге:
. В итоге: 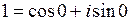 .
.
Пример 15. Представить в тригонометрической форме число z = – i.
Для него a = 0, b = –1. Следовательно, 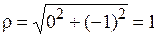 и система (1.1) имеет вид:
и система (1.1) имеет вид: 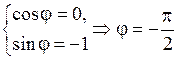 . Отсюда
. Отсюда 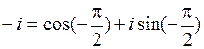 .
.
Пример 16. Представить в тригонометрической форме число z = –1.
Для числа z = –1 a = –1, b = 0. Следовательно, 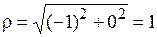 и система (1.1) имеет вид
и система (1.1) имеет вид 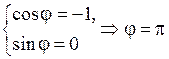 . Получаем
. Получаем 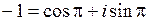 .
.
Пример 17. Представить в тригонометрической форме число z = 1 + i.
Для него a = 1, b = 1. Следовательно, 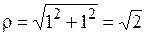 и по системе (1.1)
и по системе (1.1) 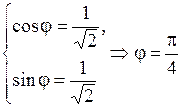 . Значит,
. Значит, 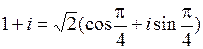 .
.
Пример 18. Представить в тригонометрической форме число z = –5 + 7 i.
Для него a = –5, b = 7. Следовательно, 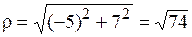 и система (1.1) принимает вид
и система (1.1) принимает вид 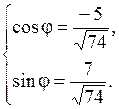 Решением этой системы будет
Решением этой системы будет
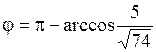 . Тогда
. Тогда
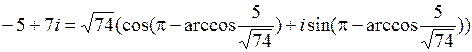 .
.
3.1.6. Умножение и деление комплексных чисел. Формула Муавра
Пусть 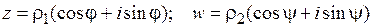 . Тогда верны формулы:
. Тогда верны формулы:
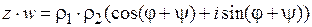 ,
,
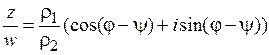 , (1.2)
, (1.2)
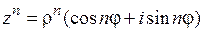 . (1.3)
. (1.3)
Последняя формула называется формулой Муавра [1, с. 190]. Она верна для любого натурального n.
Пример 19. Вычислить: 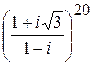 .
.
Решение. Переведем числитель и знаменатель дроби из алгебраической формы в тригонометрическую.
Для числа 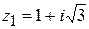
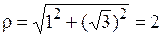 ,
, 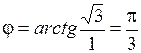 .
.
Для числа 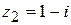
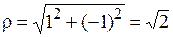 ,
, 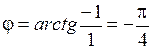 . Таким образом,
. Таким образом, 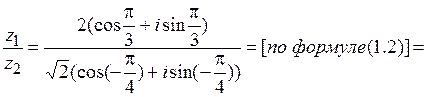
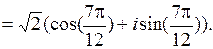
В итоге:
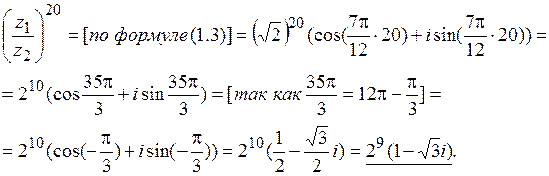
3.1.7. Задачи на построение областей на комплексной плоскости
Пример 20. Изобразить на комплексной плоскости числа, модуль которых равен 1, т. е. 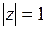 .
.
Решение. Запишем комплексное число в алгебраической форме 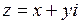 . По условию задачи интерес представляют те числа, модуль которых равен 1, т. е.
. По условию задачи интерес представляют те числа, модуль которых равен 1, т. е. 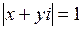 . По определению модуля комплексного числа
. По определению модуля комплексного числа 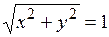 . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим 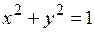 . Данное уравнение определяет на плоскости окружность с центром в точке с координатами (0; 0) и радиусом, равным 1.
. Данное уравнение определяет на плоскости окружность с центром в точке с координатами (0; 0) и радиусом, равным 1.
Пример 21. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству 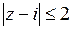 .
.
Запишем комплексное число в общем виде 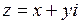 . По условию задачи, интерес представляют те числа, модуль которых меньше или равен 2, т. е.
. По условию задачи, интерес представляют те числа, модуль которых меньше или равен 2, т. е. 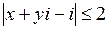 . Сгруппируем под знаком модуля слагаемые, содержащие
. Сгруппируем под знаком модуля слагаемые, содержащие 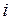 :
: 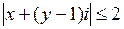 . По определению модуля комплексного числа:
. По определению модуля комплексного числа: 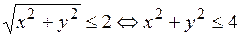 .
.
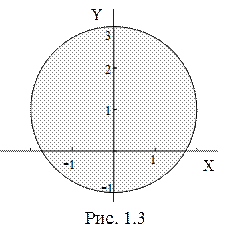
Данное уравнение определяет на плоскости круг с центром в точке с координатами (0; 1) и радиусом равным 2 (рис. 1.3).
Пример 22. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству 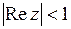 .
.
Re z – действительная часть числа z, 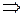 неравенство можно записать как
неравенство можно записать как 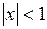 , или
, или 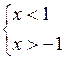 или
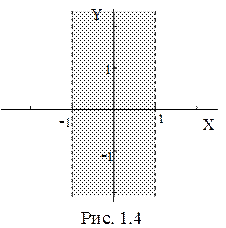
или 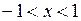 . Эта система определяет на плоскости полосу, ограниченную прямыми x = 1 и x = ‑1. Причем, обе прямые нарисованы на штрихами, так как сами прямые в искомую область не входят из-за строгого знака неравенства (рис. 1.4).
. Эта система определяет на плоскости полосу, ограниченную прямыми x = 1 и x = ‑1. Причем, обе прямые нарисованы на штрихами, так как сами прямые в искомую область не входят из-за строгого знака неравенства (рис. 1.4).
Пример 23. Найти геометрическое место точек, изображающих числа z, удовлетворяющие системе неравенств 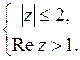
Как показано в примерах 20 и 21, неравенство 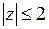 определяет на плоскости круг с центром в точке (0; 0) и радиусом, равным 2. Неравенство
определяет на плоскости круг с центром в точке (0; 0) и радиусом, равным 2. Неравенство 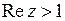 , согласно примеру 22, определяет полуплоскость, ограниченную прямой x = 1 и находящуюся от нее справа. Так как неравенство
, согласно примеру 22, определяет полуплоскость, ограниченную прямой x = 1 и находящуюся от нее справа. Так как неравенство 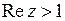 строгое, то сама прямая x = 1 в область не входит и штрихами
строгое, то сама прямая x = 1 в область не входит и штрихами
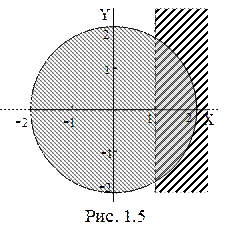
пунктиром. Обе эти области изображены на рис. 1.5. Искомая область представляет собой пересечение двух данных областей (рис. 1.6).
 Пример 24. Найти геометрическое место точек, изображающих числа z, удовлетворяющие системе неравенств
Пример 24. Найти геометрическое место точек, изображающих числа z, удовлетворяющие системе неравенств
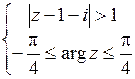 .
.
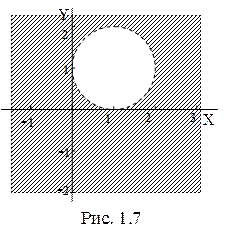
Неравенство 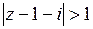 определяет область вне круга с центром в точке (1; 1) и радиусом 1. Так как неравенство строгое, то сама окружность в область не входит и изображена штрихами (рис. 1.7).
определяет область вне круга с центром в точке (1; 1) и радиусом 1. Так как неравенство строгое, то сама окружность в область не входит и изображена штрихами (рис. 1.7).
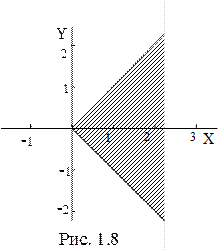
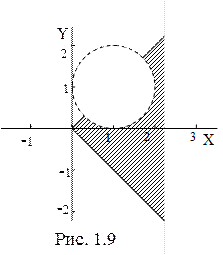
Двойное неравенство 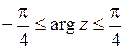 определяет на плоскости область, в которую входят комплексные числа с аргументами в интервале от
определяет на плоскости область, в которую входят комплексные числа с аргументами в интервале от 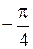 до
до 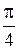 . Эта область представляет собой угол (рис. 1.8).
. Эта область представляет собой угол (рис. 1.8).
Искомая область представляет собой пересечение двух данных областей (рис. 1.9).
3.1.8. Извлечение корня из комплексных чисел
в тригонометрической форме
Определения и утверждения к 3.1.8 можно найти в [1, с. 191-192].
Комплексное число 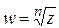 называется корнем n -й степени из комплексного числа z, если
называется корнем n -й степени из комплексного числа z, если 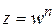 .
.
Утверждение. При любом натуральном n > 1 и любом комплексном z существует ровно n различных чисел 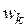 , таких, что
, таких, что 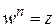 :
:
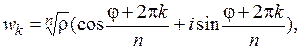 (1.4)
(1.4)
где k = 0, 1, 2,..., n – 1.
Пример 25. Вычислить 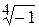 .
.
Решение. Для того чтобы воспользоваться формулой (1.4), необходимо представить число, стоящее под знаком корня, в тригонометрической форме. Для числа z = ‑1 найдем его модуль и аргумент: 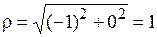 ,
,  . В итоге
. В итоге 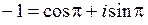 .
.
По формуле (1.4) 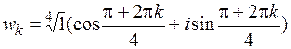 . Тогда:
. Тогда:
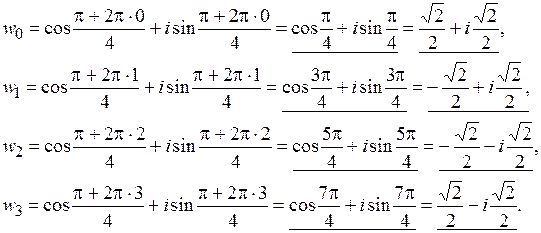
Пример 26. Вычислить 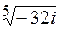 .
.
Решение. Для числа 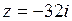 найдем его модуль
найдем его модуль  и аргумент
и аргумент 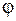 :
: 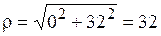 ,
, 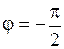 , так как число
, так как число 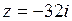 лежит на отрицательной части мнимой оси. В итоге
лежит на отрицательной части мнимой оси. В итоге 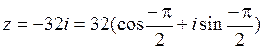 . По формуле (1.4)
. По формуле (1.4) 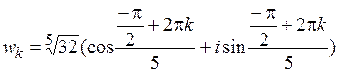 ,
,
где k = 0, 1, 2, 3, 4. Тогда:
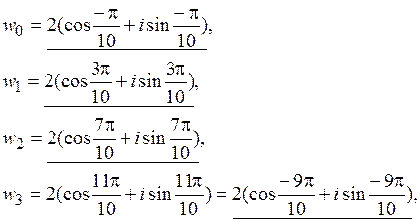
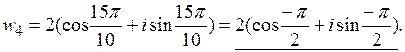
Для 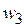 и
и 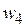 аргументами будут
аргументами будут 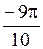 и
и 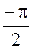 , а не
, а не 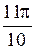 и
и 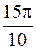 соответственно, так как
соответственно, так как 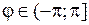 .
.
Пример 27. Вычислить 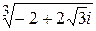 .
.
Решение. Для числа 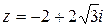 модуль
модуль 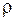 и аргумент
и аргумент 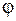 есть:
есть: 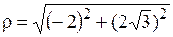 =
= 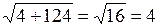 ,
, 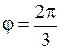 .
.
В итоге 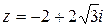 =
= 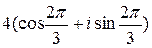 . По формуле (1.4)
. По формуле (1.4)
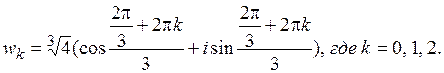 Тогда:
Тогда:
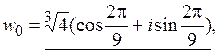
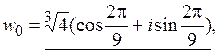
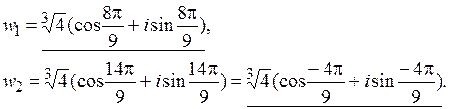
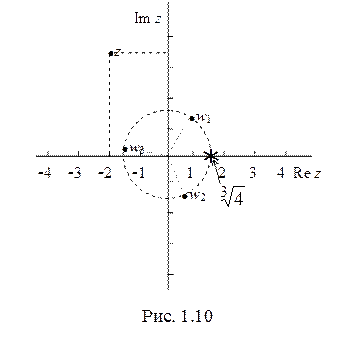 Из формулы (1.4) видно, что аргументы корней
Из формулы (1.4) видно, что аргументы корней 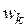 отличаются на одну и ту же величину
отличаются на одну и ту же величину 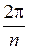 , а модули всех корней одинаковые и равны
, а модули всех корней одинаковые и равны 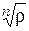 . Значит, на комплексной плоскости все
. Значит, на комплексной плоскости все 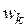 лежат на окружности с центром в начале координат и радиусом
лежат на окружности с центром в начале координат и радиусом 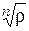 на одинаковом расстоянии друг от друга. Для примера 27 изображения самого числа
на одинаковом расстоянии друг от друга. Для примера 27 изображения самого числа 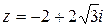 и его корней
и его корней 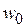 ,
, 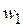 ,
, 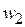 можно видеть на рис. 1.10.
можно видеть на рис. 1.10.
2. МНОГОЧЛЕНЫ
2.1. Многочлены и действия над ними
Определения и утверждения к 2.1 можно найти в [1, с. 203-206].
Для действительной переменной x функция вида 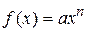 , где a и x –действительные числа, а n – натуральное число или 0 (по-другому это можно записать как
, где a и x –действительные числа, а n – натуральное число или 0 (по-другому это можно записать как 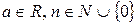 ), называется одночленом с действительным коэффициентом.
), называется одночленом с действительным коэффициентом.
Многочлен ‑ это сумма одночленов, т.е. функция вида
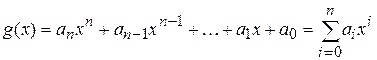 .
.
При этом 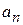 называется старшим коэффициентом и
называется старшим коэффициентом и 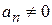 ,
, 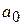 ‑ свободным членом, n ‑ степенью многочлена.
‑ свободным членом, n ‑ степенью многочлена.
Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.
Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.
На множестве многочленов определены следующие действия:
1. Сложение.
Пример 28. 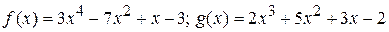 . Найти
. Найти 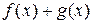 .
.
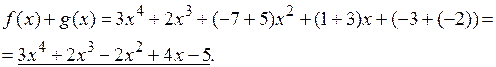
2. Умножение.
Пример 29. 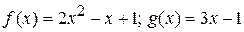 . Найти
. Найти 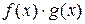 .
.
3. Деление с остатком.
Разделить 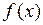 на
на 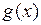 ‑ значит записать
‑ значит записать 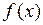 в виде
в виде  , или
, или 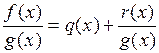 . Последняя запись аналогична записи для чисел:
. Последняя запись аналогична записи для чисел: 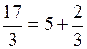 , или 17 = 5 × 3 + 2.
, или 17 = 5 × 3 + 2.
Теорема (о делении с остатком) [1, с. 206]. Для любых многочленов 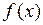 и
и 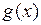
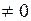 существуют, и притом единственные, многочлены
существуют, и притом единственные, многочлены 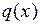 и
и 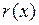 , такие, что
, такие, что
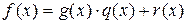 . (2.1)
. (2.1)
При этом степень 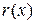 меньше степени
меньше степени 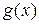 ,
, 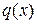 ‑ неполное частное,
‑ неполное частное, 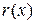 ‑ остаток. Разделить
‑ остаток. Разделить 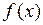 на
на 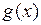 ‑ значит записать
‑ значит записать 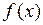 в виде (2.1).
в виде (2.1).
Для практического нахождения частного и остатка существует метод деления «уголком».
Пример 30. Выполнить «уголком» деление с остатком:
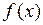 =
= 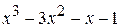 на
на 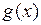 =
= 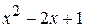 .
.

 Решение. Запишем делимое
Решение. Запишем делимое 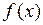 и делитель
и делитель 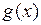 как при делении многозначных чисел:
как при делении многозначных чисел:
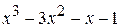
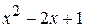
Находим частное от деления старшего члена делимого на старший член делителя (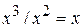 ) и записываем результат в графу частного:
) и записываем результат в графу частного:


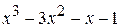
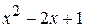
x
Умножаем делитель на результат деления и записываем под делимым:



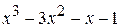
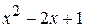
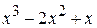 x
x
Вычитаем из делимого результат умножения:



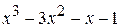
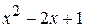

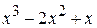 x
x
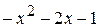
Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:



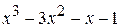
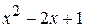

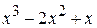 x ‑ 1
x ‑ 1

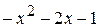
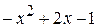
 ‑ 4 x
‑ 4 x
Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: 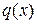 = x – 1– неполное частное, а
= x – 1– неполное частное, а
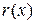 = –4 x – остаток.
= –4 x – остаток.
Ответ: 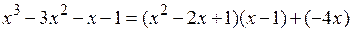 , или
, или

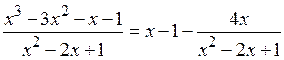 .
.
Пример 31. Выполнить деление с остатком: 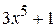 на
на 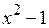 .
.
Решение. Запишем делимое и делитель как при делении многозначных чисел. Если в записи многочлена отсутствует одна или несколько степеней, то при записи, для удобства вычислений, следует на их места записать нули:



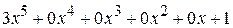
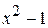


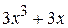

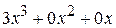


3 x +1
Получившиеся в результате умножения многочлены удобнее записывать, располагая слагаемые в соответствии с их степенями. Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: 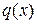 =
= 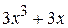 – неполное частное, а
– неполное частное, а 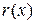 = 3 x + 1 – остаток.
= 3 x + 1 – остаток.
Ответ: 
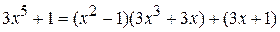 , или
, или 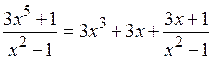 .
.
Пример 32. Делится ли нацело многочлен 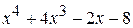 на многочлен
на многочлен 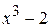 ?
?
Решение. Разделим один многочлен на другой «уголком».



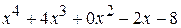
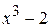


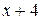




0
В остатке от деления получился нуль, значит, многочлен 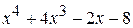 делится на многочлен
делится на многочлен 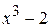 нацело и возможны записи:
нацело и возможны записи:
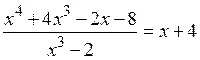 , или
, или 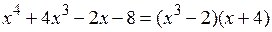 .
.
2.2. Корни многочленов
Определения и утверждения к 2.2 можно найти в [1, с. 203-206].
Корнем многочлена 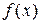 называется число
называется число 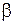 такое что
такое что 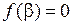 .
.
Теорема Безу. Для любой функции 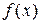 и числа
и числа 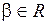 верно равенство:
верно равенство:
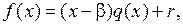
где 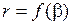 .
.
Следствие. Число 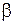 является корнем тогда и только тогда, когда
является корнем тогда и только тогда, когда 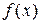 делится на
делится на 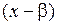 без остатка.
без остатка.
Удобной для деления на многочлены вида (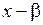 ) является схема Горнера. Рисуем таблицу, в первой строке которой записываем все коэффициенты
) является схема Горнера. Рисуем таблицу, в первой строке которой записываем все коэффициенты 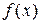 (включая нулевые).
(включая нулевые).
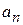
| 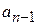
| 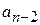
| … | 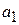
| 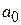
| |
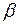
| 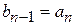
| 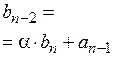
| 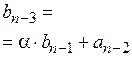
| … | 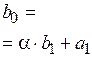
| 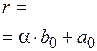
|
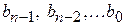 ‑ коэффициенты неполного частного от деления
‑ коэффициенты неполного частного от деления  на (
на (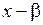 );
); 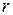 ‑ остаток от деления, который по теореме Безу равен
‑ остаток от деления, который по теореме Безу равен 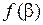 . Если
. Если 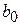 = 0, то говорят, что
= 0, то говорят, что 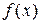 делится на (
делится на (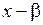 ) нацело и
) нацело и 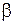 ‑ корень многочлена
‑ корень многочлена 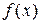 .
.
Пример 33. Разделить 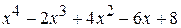 на
на 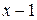 .
.
Решение. Воспользуемся схемой Горнера. Нарисуем таблицу и выполним расчеты.
| ‑2 | ‑6 | ||||
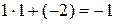
| 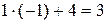
| 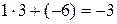
| 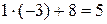
|
Итак, 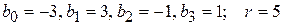 , где
, где 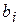 ‑ коэффициенты неполного частного. Следовательно,
‑ коэффициенты неполного частного. Следовательно, 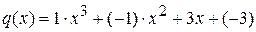 .
.
Ответ: 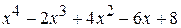 =
= 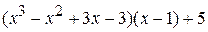 .
.
Пример 34. Найти значение функции 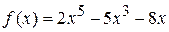 в точке
в точке
x = ‑2.
Решение. С помощью схемы Горнера разделим 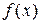 на многочлен
на многочлен 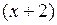 . При заполнении таблицы учитываем, что коэффициенты при четвертой и второй степенях, а также свободный член в многочлене равны 0.
. При заполнении таблицы учитываем, что коэффициенты при четвертой и второй степенях, а также свободный член в многочлене равны 0.
| ‑5 | ‑8 | |||||
| ‑2 | 2 
| 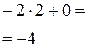
| 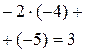
| 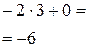
| 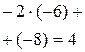
| 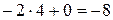
|
В результате вычислений получили остаток, равный ‑8. По теореме Безу он равен значению 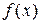 в точке x = ‑2.
в точке x = ‑2.
Ответ: {–8}.
Алгоритм деления, рассмотренный в 2.1, применим для деления на многочлен любой степени, а схема Горнера применима только для деления на (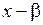 ).
).
2.3. Неприводимые многочлены
Определения и утверждения к 2.3 можно найти в [1, с. 204-206]. Многочлен с действительными коэффициентами 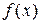 является неприводимым, если не существует многочленов
является неприводимым, если не существует многочленов 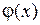 и
и 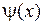 с действительными коэффициентами степени меньшей
с действительными коэффициентами степени меньшей 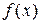 , таких, что
, таких, что 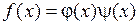 . Т. е. неприводимый многочлен нельзя разложить в произведение многочленов меньших степеней.
. Т. е. неприводимый многочлен нельзя разложить в произведение многочленов меньших степеней.
Утверждение. Неприводимыми многочленами с действительными коэффициентами являются многочлены 1-й или 2-й степени с отрицательным дискриминантом, и только они.
Разложением многочлена на множители называется представление его в виде произведения неприводимых многочленов.
Основные методы разложения многочленов на множители:
1. Вынесение общего множителя за скобки.
2. Использование формул сокращенного умножения.
Пример 35. Разложить на множители многочлен 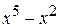 .
.
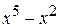 =
= 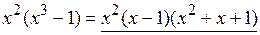 . При разложении воспользовались формулой
. При разложении воспользовались формулой 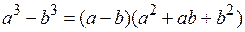 .
.
3. Метод группировки.
Пример 36. Разложить на множители многочлен 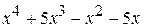 .
.
Группируем вместе слагаемые, содержащие множитель 5:
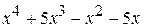 =
= 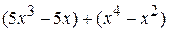 =
= 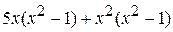 =
=
= [вынесем общий множитель за скобки] =
= 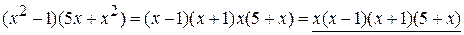 .
.
Пример 37. Разложить на множители многочлен 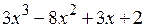 .
.
Группируем слагаемые, начиная с первого:
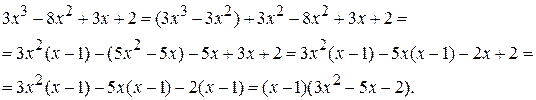
Квадратный трехчлен раскладываем на множители, найдя его корни:
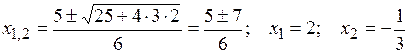 . Тогда:
. Тогда:
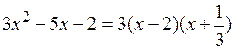 . В итоге
. В итоге
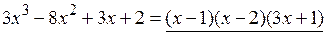 .
.
4. Метод подбора корней.
Этот метод основан на следующих утверждениях:
Утверждение 1. Если для многочлена
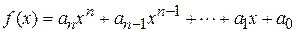 числа
числа 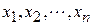 ‑ корни, то верно равенство
‑ корни, то верно равенство 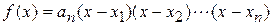 .
.
Утверждение 2. У многочлена со старшим коэффициентом, равным 1, целыми корнями могут быть только делители свободного члена.
Пример 38. Возможными целыми корнями многочлена 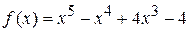 могут быть числа
могут быть числа 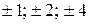 . Методом подбора можно установить, что
. Методом подбора можно установить, что 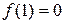 и, следовательно, 1 ‑ корень многочлена.
и, следовательно, 1 ‑ корень многочлена.
Пример 39. Разложить на множители многочлен 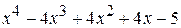 .
.
Решение. Согласно утверждению 2 возможными целыми корнями многочлена могут быть только делители числа ‑5. Это числа 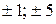 . Найдем значение многочлена в точке x = ‑ 1:
. Найдем значение многочлена в точке x = ‑ 1:
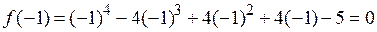 . Следовательно, корнем многочлена
. Следовательно, корнем многочлена 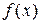 является x = ‑1. Разделим многочлен
является x = ‑1. Разделим многочлен 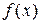 на (x + 1). По теореме Безу,
на (x + 1). По теореме Безу, 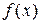 должен делиться на (x + 1) нацело, то есть, остаток от деления должен равняться нулю. Для деления воспользуемся схемой Горнера.
должен делиться на (x + 1) нацело, то есть, остаток от деления должен равняться нулю. Для деления воспользуемся схемой Горнера.
| ‑4 | ‑5 | ||||
| ‑1 | 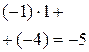
| (‑1)(‑5) + + 4 = 9 | 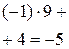
| 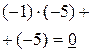
|
Число, получившееся в последнем столбце, позволяет проверить правильность вычислений. Если получен нуль, значит, все вычисления верны. Если число в последнем столбце отлично от нуля, значит, или корень найден неверно, или вычисления по схеме Горнера проведены неправильно.
Итак: 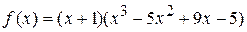 . Поскольку получившийся в результате деления многочлен
. Поскольку получившийся в результате деления многочлен 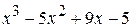 не является неприводимым, то процесс разложения на множители необходимо продолжить. Для многочлена
не является неприводимым, то процесс разложения на множители необходимо продолжить. Для многочлена 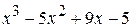 возможными корнями будут числа
возможными корнями будут числа 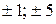 . Находим:
. Находим: 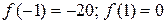 . Следовательно, 1 ‑ корень многочлена
. Следовательно, 1 ‑ корень многочлена 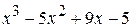 . Разделим его на (x ‑ 1) по схеме Горнера.
. Разделим его на (x ‑ 1) по схеме Горнера.
| ‑5 | ‑5 | |||
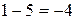
| 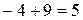
| 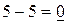
|
В последнем столбце получился нуль. Значит, вычисления верны.
Имеем: 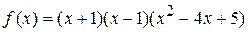 . Проверим, является ли многочлен
. Проверим, является ли многочлен 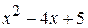 неприводимым. Найдем его корни по стандартной формуле:
неприводимым. Найдем его корни по стандартной формуле:
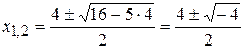 . Так как дискриминант данного квадратного трехчлена отрицателен, он является неприводимым на множестве действительных чисел.
. Так как дискриминант данного квадратного трехчлена отрицателен, он является неприводимым на множестве действительных чисел.
Ответ: 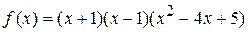 .
.
2.4. Нахождение наибольшего общего делителя многочленов
Определение. Если каждый из двух многочленов делится без остатка на третий, то он называется общим делителем первых двух.
Наибольшим общим делителем (НОД) двух многочленов называется их общий делитель наивысшей степени.
НОД можно находить с помощью разложения на неприводимые множители или с помощью алгоритма Евклида.
Пример 40. Найти НОД многочленов 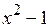 и
и 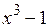 .
.
Решение. Разложим оба многочлена на множители:
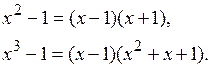
Из разложения видно, что искомым НОДом будет многочлен (х – 1).
Пример 41. Найти НОД многочленов 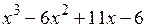 и
и 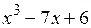 .
.
Решение. Разложим оба многочлена на множители.
Для многочлена 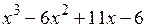 возможными рациональными корнями будут числа ±1, ±2, ±3 и ±6. С помощью подстановки убеждаемся, что х = 1 является корнем. Разделим многочлен на (х – 1) по схеме Горнера.
возможными рациональными корнями будут числа ±1, ±2, ±3 и ±6. С помощью подстановки убеждаемся, что х = 1 является корнем. Разделим многочлен на (х – 1) по схеме Горнера.
| –6 | –6 | |||
| 1 – 6 = –5 | –5 + 11 = 6 | 6 – 6 = 0 |
Следовательно, 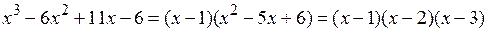 , где разложение квадратного трехчлена
, где разложение квадратного трехчлена 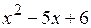 было произведено по теореме Виета.
было произведено по теореме Виета.
Для многочлена 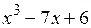 возможными рациональными корнями будут числа ±1, ±2, ±3 и ±6. С помощью подстановки убеждаемся, что х = 1 является корнем. Разделим многочлен на (х – 1) по схеме Горнера.
возможными рациональными корнями будут числа ±1, ±2, ±3 и ±6. С помощью подстановки убеждаемся, что х = 1 является корнем. Разделим многочлен на (х – 1) по схеме Горнера.
| –7 | ||||
| 1 – 0 = 1 | 1 – 7 = –6 | –6 + 6 = 0 |
Следовательно, 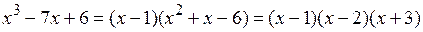 , где разложение квадратного трехчлена
, где разложение квадратного трехчлена 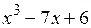 было произведено по теореме Виета.
было произведено по теореме Виета.
Сравнив разложение многочленов на множители, находим, что искомым НОДом будет многочлен (х – 1)(х – 2).
Аналогично можно находить и НОД для нескольких многочленов.
Тем не менее, метод нахождения НОДа путем разложения на множители доступен не всегда. Способ, позволяющий находить НОД для всех случаев, называется алгоритмом Евклида.
Схема алгоритма Евклида такова. Один из двух многочленов делят на другой, степень которого не выше степени первого. Далее, за делимое всякий раз берут тот многочлен, который служил в предшествующей операции делителем, а за делитель берут остаток, полученный при той же операции. Этот процесс прекращается, как только остаток окажется равным нулю. Покажем этот алгоритм на примерах.
Рассмотрим многочлены, использовавшиеся в двух предыдущих примерах.
Пример 42. Найти НОД многочленов 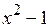 и
и 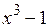 .
.
Решение. Разделим 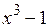 на
на 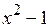 «уголком»:
«уголком»:


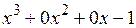
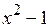


 x
x
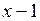
Теперь разделим делитель 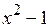 на остаток х – 1:
на остаток х – 1:



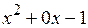
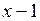

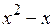 x + 1
x + 1

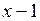

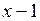
Так как последнее деление произошло без остатка, то НОДом будет х – 1, т. е. многочлен, использовавшийся в качестве делителя при этом делении.
Пример 43. Найти НОД многочленов 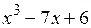 и
и 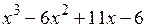 .
.
Решение. Для нахождения НОД воспользуемся алгоритмом Евклида. Разделим 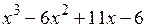 на
на 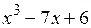 «уголком»:
«уголком»:

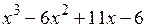
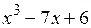



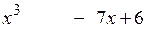 1
1
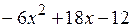
Произведем второе деление. Для этого пришлось бы разделить предыдущий делитель 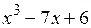 на остаток
на остаток 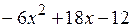 , но так как
, но так как 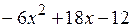 =
= 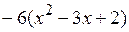 , для удобства будем делить многочлен
, для удобства будем делить многочлен 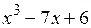 не на
не на 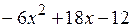 , а на
, а на 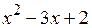 . От такой замены решение задачи не изменится, так как НОД пары многочленов определяется с точностью до постоянного множителя. Имеем:
. От такой замены решение задачи не изменится, так как НОД пары многочленов определяется с точностью до постоянного множителя. Имеем:



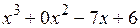
Date: 2015-07-02; view: 1035; Нарушение авторских прав