
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Эйлера
|
|
Воспользуемся разложением в ряд Тейлора-Маклорена функций:
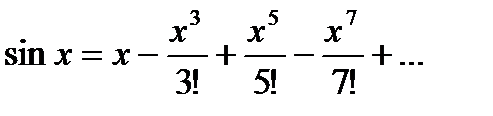
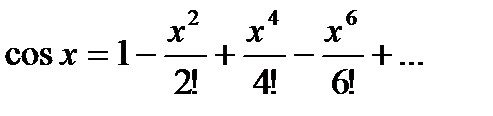
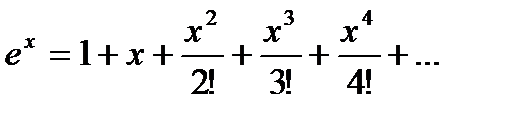
В последнюю формулу вместо 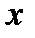 подставим
подставим 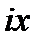 :
:
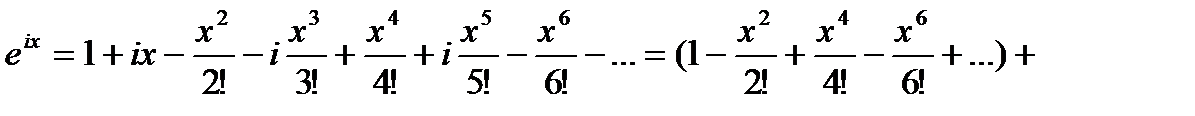
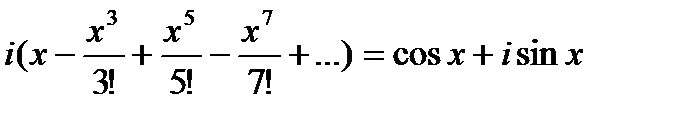 (9)
(9)
Тогда 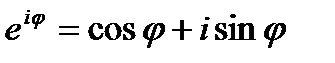 - формула Эйлера.
- формула Эйлера.
Подставив в формулу 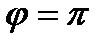 , получим соотношение между числами:
, получим соотношение между числами: 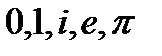 .
.
А именно 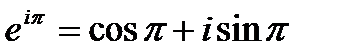
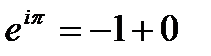 ,
, 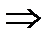
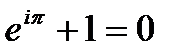
Используя формулу Эйлера, была получена показательная форма комплексного числа:
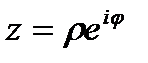 (10)
(10)
Тогда: 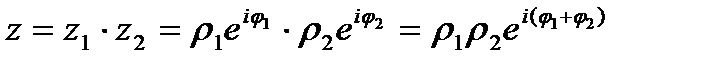 (11)
(11)
Последнее равенство подтверждает правило для вычисления произведения комплексных чисел: модули перемножаются, аргументы суммируются.
Используя формулу произведения комплексных чисел в а) показательной и б) тригонометрической формах, легко получить форму возведения в степень:
а) 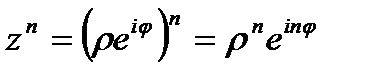 ,
,
б) 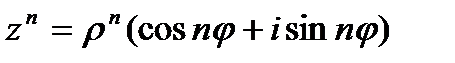 - формула Муавра (12)
- формула Муавра (12)
Аналогично 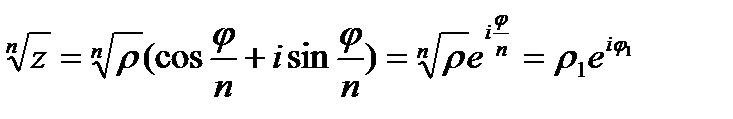 . (13)
. (13)
Следует заметить, что для нахождения угла 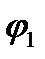 требуется учитывать не только полярный угол
требуется учитывать не только полярный угол 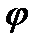 , но и период
, но и период 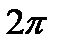 , т.е.
, т.е.  . (14)
. (14)
Задача 5.1. Найти значение выражения 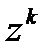 , для
, для  ; а)
; а) 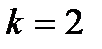 ; б)
; б) 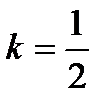 .
.
 Решение. По формуле (6)
Решение. По формуле (6) 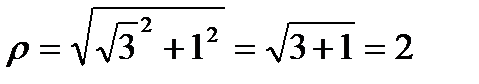 . Воспользовавшись формулой (7), получим:
. Воспользовавшись формулой (7), получим: 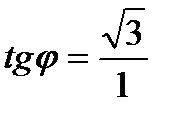
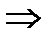
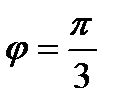 . Запишем заданное число в показательной форме:
. Запишем заданное число в показательной форме: 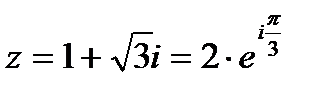 .
.
Найдем 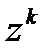 .
.
а) 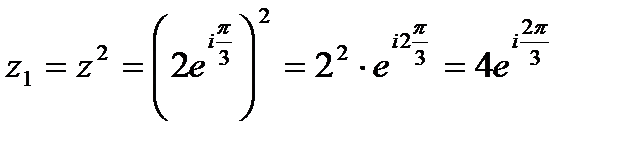 .
.
| Рис.11 |
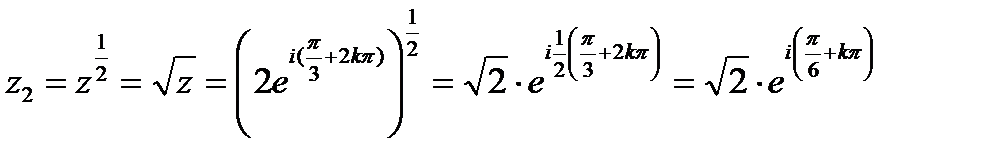 .
.
Тогда, если 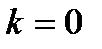 :
: 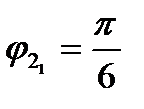 ;
;
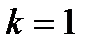 :
: 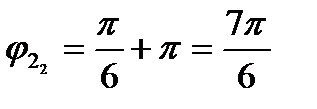 ;
;
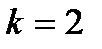 :
: 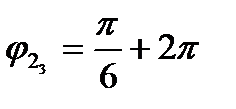 - графическое изображение совпадает с
- графическое изображение совпадает с 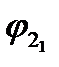 , все следующие углы будут повторять уже найденные.
, все следующие углы будут повторять уже найденные.
Итого, 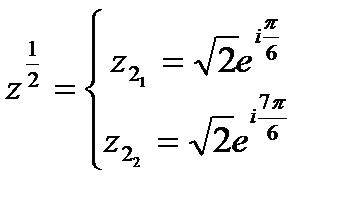 .
.
Задача 5.2. Найти 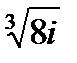 .
.
Решение. 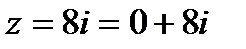 . По формулам (6) и (7) получим:
. По формулам (6) и (7) получим:
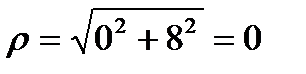 ,
, 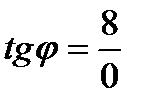 ,
, 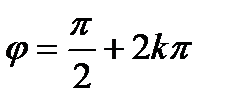 .
.
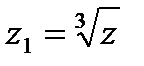
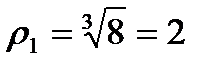 .
.
По формуле (14) получим: 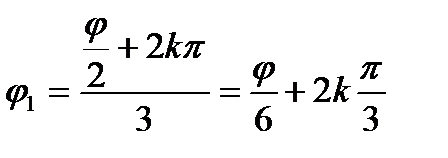 .
.
Тогда:
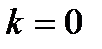 :
: 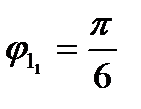 ;
;
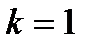 :
: 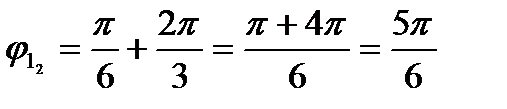 ;
;
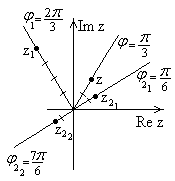
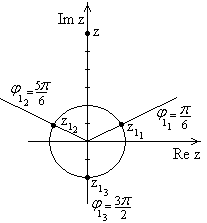
| Рис.12 |
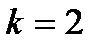 :
: 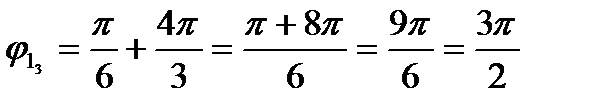 ;
;
 :
: 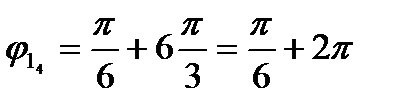 - графическое изображение совпадает с
- графическое изображение совпадает с 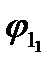 . Т.к. для всех корней (
. Т.к. для всех корней (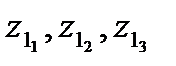 )
) 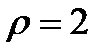
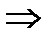 они лежат на окружности радиуса 2.
они лежат на окружности радиуса 2.
Найдем алгебраическую форму этих корней:
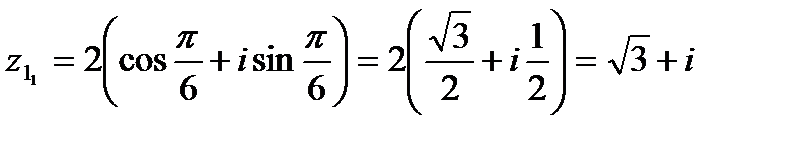 ;
;
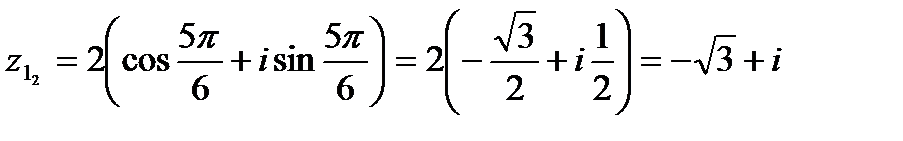 ;
;
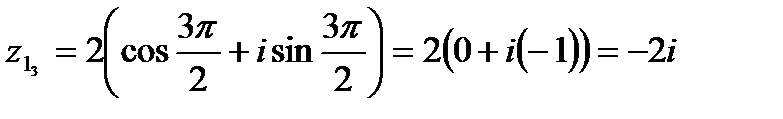 .
.
Date: 2015-07-02; view: 563; Нарушение авторских прав