Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Пример решения типовой задачи

⇐ ПредыдущаяСтр 10 из 10




Пусть даны два электроприемника с периодическими индивидуальными графиками электрической нагрузки по активной мощности s w:val="28"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>t</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 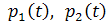показанными на рис.3.3

t
Рс1=3,5 кВт
 
 
 
 
р1(t)
кВт
час
 
 
 
 
 
 
 
 
 
р2(t)  
кВт  
 
 
 
 
 
 
 
 
 
 
 
 
Рс2=4 кВт
 
 
 
 
час
t

 


Рис. 3.3 Индивидуальные графики электрической нагрузки электроприемников s w:val="28"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>t</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">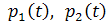

Длительности циклов графиков s w:val="28"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>t</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 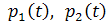одинаковы 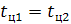= 4час. Одинаковы также длительности ступеней графиков .

Определим числовые характеристики графиков s w:val="28"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>t</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">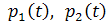

Математические ожидания(средние значения):

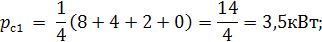
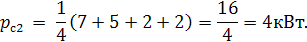
Дисперсии графиков :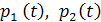

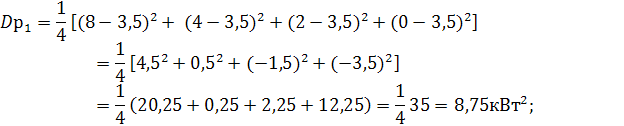
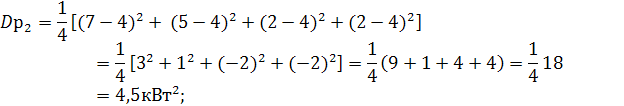
Эффективные (действующие) значения графиков:

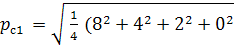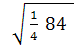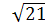) = = = = 4,58 кВт;

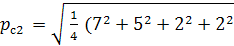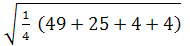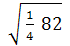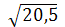) = = = = 4,53кВт.

Дисперсии графиков по формуле - :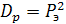

.

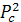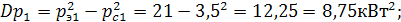
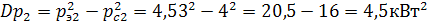Построим суммарный график 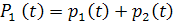при нулевом сдвиге во времени и определим его характеристики. Среднее значение суммарного графика

.

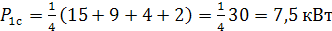Среднее значение суммарного графика равно сумме средних значений суммарных графиков:

.

 

 

 
 
 
 
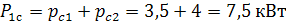t
Р∑с1=7,5 кВт
DР∑1=8,75 кВт2
кВт
час
 
 
 
 
 
 
 
 
 
 
 
 
 
P∑1 (t)
W=30 кВт·ч
Р∑с1=7,5 кВт
DР∑2=4,5 кВт2
час
 
 
 
 
 
P∑2 (t)
кВт
 
 
 
 
 
 
 
 
 
t
W=30 кВт·ч

 

 


Рис. 3.4. Суммарные графики электрической нагрузки t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>. </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">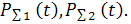

 

Эффективное значение суммарного графика:

;

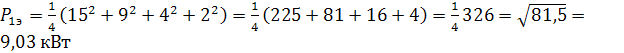Дисперсия суммарного графика:

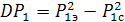= 81,5- .

Для определения сдвига во времени между графиками, при котором дисперсия будет минимальной построим зависимость корреляционной функции графиков s w:val="28"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>t</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 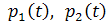от сдвига m = 0,1,2,3,4.

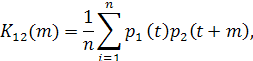
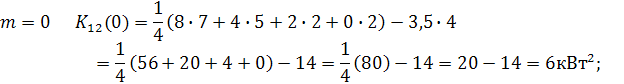
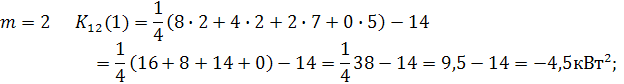
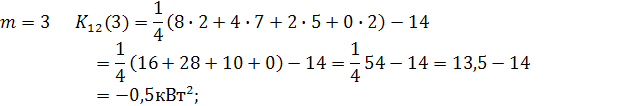
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">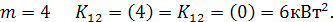

Построим график функции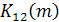

K12(m)
кВт2
час
 
 
 
 
 
-4
-2
 
 
 
 
-6
-1
-4,5
-0,5
m

 


Дисперсия суммарного графика может быть вычислена также с использованием дисперсий индивидуальных графиков и взаимнокореляционной функции 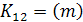по формуле:

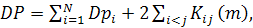(3.3)

где N – число суммируемых графиков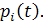

Для N = 2 эта формула имеет вид:

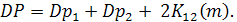(3.4)

Проверим эту формулу и расчеты 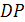и ВКФ 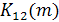для графика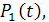

для которого дисперсия равна .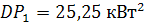

.

Из формулы (3.4) и графика ВКФ 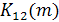, рис3.4 следует, что если электроприемники №1 и №2 c графиками 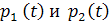будут работать со сдвигом во времени m = 2, при котором 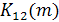имеет наименьшее значение, то дисперсия 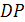будет минимальной.

Построим суммарный график 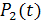при сдвиге во времени второго графика на m = 2 часа. =

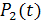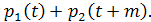
Определим характеристики графика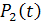

;

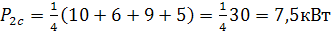Среднее значение суммарного графика не зависит от сдвига во времени индивидуальных графиков :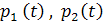

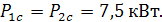
Эффективное значение графика :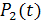

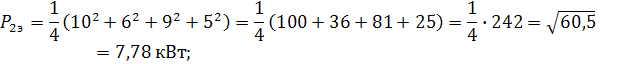
Дисперсия графика :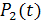

.

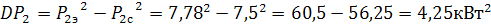Определим дисперсию графика 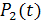по формуле (3.4)

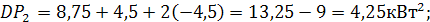
Таким образом, с помощью графики ВКФ 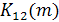можно найти сдвиг во времени между индивидуальными графиками 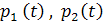суммарный график будет иметь наименьшую дисперсию.

Сопоставим характеристики графиков 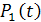и :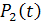

 

Таблица 3.1. Характеристики суммарных графиков ,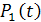

 

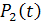
  График Среднее значение кВт Эффективное значе-ние кВт   Дисперсия кВт2 Среднеквадра-тическое откло-нение кВт Максималь-ное значе- ние кВт
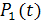
7,5 9,03 25,25 5,02  
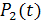
7,5 7,78 4,25 2,06  

 

Влияние формы графика электрической нагрузки на потери электроэнергии.

 

 

I(t)
час
 
Ic
t
T
I(t)
P(t)
i2(t)
P2(t)
 
P1(t)
i1(t)
R
 

 

 

 

 


 

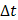
Рис. Рис.

 

 

Потери мощности 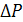и потери электроэнергии за время 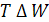в трехфазной линии питающей два электроприемника с графиками электрической нагрузки по току 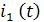и , +

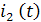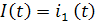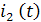
Определяются по формуле

Ток 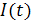в линии изменяется в соответствии с графиком показанным на рис. 3.4.

При заданном графике нагрузки 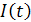потери электроэнергии можно вычислить по формуле

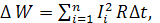
где 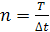- количество ступеней в графике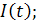

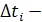длительность ступеней.

При одинаковых длительностях ступеней 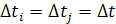формулу для 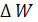можно записать следующим образом:

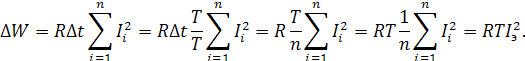
Таким образом, т.е. потери электроэнергии за время Т зависят от эффективного значения графика нагрузки по току. Выразим эффективное значение графика 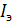через дисперсию

и подставим в формулу для :

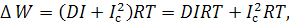
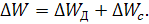
Таким образом, потери электроэнергии в линии можно разложить на две составляющие:

r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 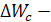потери определяемые по средней нагрузке и 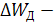потери зависящие от дисперсии графика электрической нагрузки.

Дисперсия графика 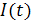определяется через характеристики график 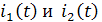следующим образом:

Отсюда

Следовательно потери электроэнергии в линии можно разложить на три составляющие, определяемые по характеристикам индивидуальных графиков:

r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 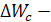потери определяемые по средним нагрузкам;

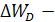потери электроэнергии, определяемые по дисперсиям нагрузок индивидуальных графиков;

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 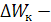потери определяемые по взаимнокорреляционным моментам графиков нагрузки .

Впервые такое представление разложения потерь электроэнергии в любой сети было дано профессором Каяловым Г.М. в 1976году в работе [5].

 

Литература

 

1. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – М.: Высш. шк., 2001. –576с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002, 480с.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002, 400с.

 

Дополнительная

 

4. Каялов Г.М. Определение потерь энергии в электрической сети по средним значениям нагрузок в ее узлах. Электричество, 1976, N 6. - с.19-24.

 


Приложение 1

 

Таблица 1 Значения функции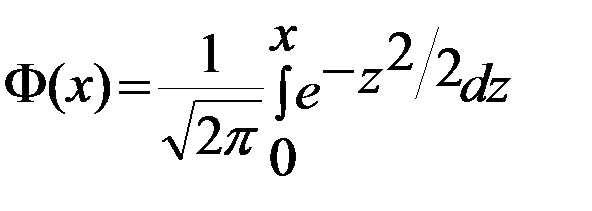

 

x Ф(х) x Ф(x) x Ф(х) x Ф (х)
0,00 0,0000 0,30 0,1179 0,60 0,2257 0,90 0,3159
0,01 0,0040 0,31 0,1217 0,61 0,2291 0,91 0,3186
0,02 0,0080 0,32 0,1255 0,62 0,2324 0,92 0,3212
0,03 0,0120 0,33 0,1293 0,63 0,2357 0,93 0,3238
0,04 0,0160 0,34 0,1331 0,64 0,2389 0,94 0,3264
0,05 0,0199 0,35 0,1368 0,65 0,2422 0,95 0,3289
0,06 0,0239 0,36 0,1406 0,66 0,2454 0,96 0,3315
0,07 0,0279 0,37 0,1443 0,67 0,2486 0,97 0,3340
0,08 0,0319 0,38 0,1480 0,68 0,2517 0,98 0,3365
0,09 0,0359 0,39 0,1517 0,69 0,2549 0,99 0,3389
0,10 0,0398 0,40 0,1554 0,70 0,2580 1,00 0,3413
0,11 0,0438 0,41 0,1591 0,71 0,2611 1,01 0,3438
0,12 0,0478 0,42 0,1628 0,72 0,2642 1,02 0,3461
0,13 0,0517 0,43 0,1664 0,73 0,2673 1,03 0,3485
0,14 0,0557 0,44 0,1700 0,74 0,2703 1,04 0,3508
0,15 0,0596 0,45 0,1736 0,75 0,2734 1,05 0,3531
0,16 0,0636 0,46 0,1772 0,76 0,2764 1,06 0,3554
0,17 0,0675 0,47 0,1808 0,77 0,2794 1,07 0,3577
0,18 0,0714 0,48 0,1844 0,78 0,2823 1,08 0,3599
0,19 0,0753 0,49 0,1879 0,79 0,2852 1,09 0,3621
0,20 0,0793 0,50 0,1915 0,80 0,2881 1,10 0,3643
0,21 0,0832 0,51 0,1950 0,81 0,2910 1,11 0,3665
0,22 0,0871 0,52 0,1985 0,82 0,2939 1,12 0,3686
0,23 0,0910 0,53 0,2019 0,83 0,2967 1,13 0,3708
0,24 0,0948 0,54 0,2054 0,84 0,2995 1,14 0,3729
0,25 0,0987 0,55 0,2088 0,85 0,3023 1,15 0,3749
0,26 0,1026 0,56 0,2123 0,86 0,3051 1,16 0,3770
0,27 0,1064 0,57 0,2157 0,87 0,3078 1,17 0,3790
0,28 0,1103 0,58 0,2190 0,88 0,3106 1,18 0,3810
0,29 0,1141 0,59 0,2224 0,89 0,3133 1.19 0,3830

 

Продолжение таблицы 1

 

 

1,20 0,3849 1,55 0,4394 1,90 0,4713 2,50 0,4938
1,21 0,3869 1,56 0,4406 1,91 0,4719 2,52 0,4941
1,22 0,3883 1,57 0,4418 1,92 0,4726 2,54 0,4945
1,23 0,3907 1,58 0,4429 1,93 0,4732 2,56 0,4948
1,24 0,3925 1,59 0,4441 1,94 0,4738 2,58 0,4951
1,25 0,3944 1,60 0,4452 1,95 0,4744 2,60 0,4953
1,26 0,3962 1,61 0,4463 1,96 0,4750 2,62 0,4956
1,27 0,3980 1,62 0,4474 1,97 0,4756 2,64 0,4959
1,28 0,3997 1,63 0,4484 1,98 0,4761 2,66 0,4961
1,29 0,4015 1,64 0,4495 1,99 0,4767 2,68 0,4963
1,30 0,4032 1,65 0,4505 2,00 0,4772 2,70 0,4965
1,31 0,4049 1,60 0,4515 2,02 0,4783 2,72 0,4967
1,32 0,4066 1,67 0,4525 2,04 0,4793 2,74 0,4969
1,33 0,4082 1,68 0,4535 2,06 0,4803 2,76 0,4971
1,34 0,4099 1,69 0,4545 2,08 0,4812 2,78 0,4973
1,35 0,4115 1,70 0,4554 2,10 0,4821 2,80 0,4974
1,36 0,4131 1,71 0,4564 2,12 0,4830 2,82 0,4976
1,37 0,4147 1,72 0,4573 2,14 0,4838 2,84 0,4977
1,38 0,4162 1,73 0,4582 2,16 0,4846 2,86 0,4979
1,39 0,4177 1,74 0,4591 2,18 0,4854 2,88 0,4980
1,40 0,4192 1,75 0,4599 2,20 0,4861 2,90 0,4981
1.41 0,4207 1,76 0,4608 2,22 0.4868 2,92 0,4982
1.42 0,4222 1,77 0,4616 2,24 0,4875 2,94 0,4984
1,43 0,4236 1,78 0,4625 2,26 0,4881 2,96 0,4985
1,44 0,4251 1.79 0,4633 2,28 0,4887 2,98 0,4986
1,45 0,4265 1,80 0,4641 2,30 0,4893 3,00 0,49865
1,46 0,4279 1,81 0,4649 2,32 0,4898 3,20 0,49931
1,47 0,4292 1.82 0,4656 2,34 0,4904 3,40 0,49966
1,48 0,4306 1,83 0,4664 2,36 0,4909 3,60 0,499841
1,49 0,4319 1,84 0,4671 2,38 0.4913 3,80 0,499928
1,50 0,4332 1.85 0,4678 2,40 0,4918 4,00 0,499968
1,51 0,4345 1,86 0,4686 2,42 0,4922 4,50 0,499997
1,52 0,4357 1,87 0,4693 2.44 0,4927 5,00 0,499997
1,53 0,4370 1,88 0,4699 2,46 0,4931    
1,54 0,4382 1,89 0,4706 2,48 0,4934    

 


⇐ Предыдущая12345678910

Date: 2015-07-01; view: 655; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.007 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию