
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерии согласия
|
|
Представим что произведено N независимых испытаний, в каждом из которых случайная величина Х приняла некоторое значение хi, i = 1,2, …, N.
Результаты испытаний сгруппированы по разрядам виде статистического ряда, следующим образом:
Таблица
| Границы разрядов гистограммы | х1; х2 | х2 ; х3 | … | хk ; хk+1 |
| Количество попаданий в разряды n i | n1 | n2 | … | nk |
В таблице 2.4 х1 , х2, … хk+1 - границы разрядов гистограммы;
k – количество разрядов гистограммы;
n1, n2,…, nk – числа попаданий случайной величины х в 1, 2, …, k -й разряды.
Таблица. Результаты измерения потребления электроэнергии
| № п/п | Электро-энергия, кВт.ч. | N п/п | Электро-энергия кВт.ч. | N п/п | Электро-энергия кВт.ч. | N п/п | Электро-энергия кВт.ч. |
На рис. 2.1 показана гистограмма распределения среднемесячного потребления электроэнергии абонентами г Новочеркасска.
Мера расхождения опытного распределения с теоретическим определяется по формуле:
χ2 = 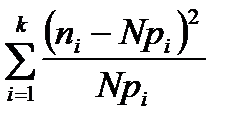 ;
;
где рi – вероятность попадания случайной величины х в i - й разряд, вычисленная его предполагаемому «теоретическому» распределению.
Распределение χ2 зависит от параметра r, называемого числом степеней свободы:
r = k – s,
где k – число разрядов гистограммы;
s – число независимых условий (связей) накладываемых на частоты ni.
К таким условиям относятся следующие:
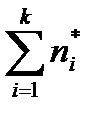 = 1 – обязательное условие равенства единице суммы частот
= 1 – обязательное условие равенства единице суммы частот 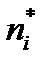 ряда;
ряда;

Рис2.1 Гистограмма среднемесячного потребления электроэнергии бытовых абонентов г. Новочеркасска за 2002 год. Объем выборки n = 672.
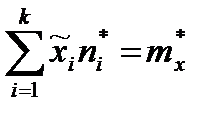 т.е.
т.е. 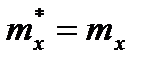 , если подбирается такой закон распределения, в котором математическое ожидание
, если подбирается такой закон распределения, в котором математическое ожидание  равно его оценке
равно его оценке 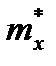 ;
;
 , т.е.
, т.е. 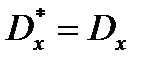 , если подбирается теоретическое распределение, дисперсия которого равна ее оценке
, если подбирается теоретическое распределение, дисперсия которого равна ее оценке 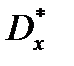 .
.
В формулах для оценок математического ожидания и дисперсии 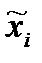 – это середина i -го разряда гистограммы.
– это середина i -го разряда гистограммы.
Задача 2.4.1 В таблице 5 приведены результаты экспериментального исследования электрической нагрузки по активной мощности Р (t) трансформатора цеховой трансформаторной подстанции (по показаниям счетчика через пятиминутные интервалы). Весь интервал наблюдаемых значений случайной величины Р разбит на разряды, границы которых указаны в таблице 4. Известны значения ni – числа попаданий случайной величины Р в i -й разряд.
1. Построить гистограмму случайной величины Р.
2. Определить числовые характеристики статистического распределения: М *[ Р ] – математическое ожидание и D *[ P ] – дисперсию.
3. С помощью критерия Пирсона выполнить проверку гипотезы о нормальном законе распределения случайной величины Р (о нормальном распределении генеральной совокупности).
Указания 1. Уровень значимости принять равным α = 0,05.
2. Для нормального закона распределения число наложенных связей равно 3 (∑ Ei = 1; D [ P ] = D *[ P ]; M [ P ] = M *[ P ]).
3. Теоретические частоты Еi для нормального закона распределения определяются по таблицам значений функций
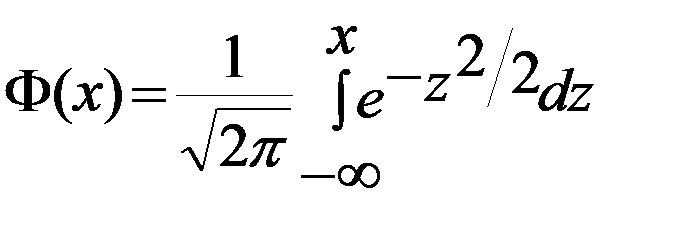 или
или 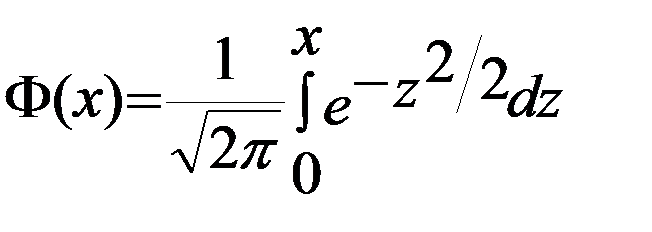
(см. Л[1], Приложение 2 или Л[2] табл. 1 Приложения).
Таблица 5.
| № варианта | Границы разрядов гистограммы, кВт | ||||||||||||
| 535-540 | 540-545 | 545-550 | 550-555 | 555-560 | 560-565 | 565-570 | 570-575 | 575-580 | 580-585 | 585-590 | 590-595 | 595-600 | |
Date: 2015-07-01; view: 582; Нарушение авторских прав