Суточный график электрической нагрузки как реализация случайного процесса

В электроэнергетике для характеристики потребителей электроэнер­гии, а также нагрузки отдельных узлов или линий электропередач использу­ются графики режимных дней, которые записываются два раза в год в июле и декабре. Такие графики считаются типовыми для исследуемого обьекта в летний и зимний периоды. На рис. 3.1 показаны суточные графики транс­форматорной подстанции 10/0,4 кВ питающей коммунально-бытовую на­грузку города.

С точки зрения теории случайных процессов такой график – это за­пись одной реализации суточного графика.

Тем не менее, на практике такие графики, т.е. отдельные реализации используют для вычисления таких характеристик как математическое ожида­ние (среднее значение РС) эффективное значение РЭ, дисперсия.

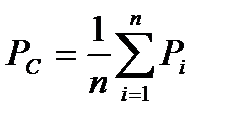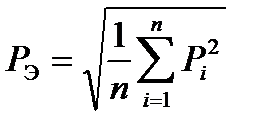; ; (3.1)

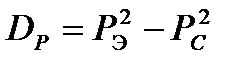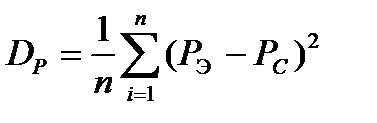; . (3.2)

Для характеристики формы графика нагрузки и степени его отклоне­ния от среднего используется также коэффициент формы кФ = РЭ / Рс, а также коэффициент заполнения кЗ =Рс / РМ – где РМ – максимальное значение гра­фика (см. рис. 3.1).

Кроме указанных характеристик для оценки зависимости нагрузок отдельных потребителей по времени суток определения взаимнокорреляци­онный момент (ВКМ) графиков Pi, Pj.

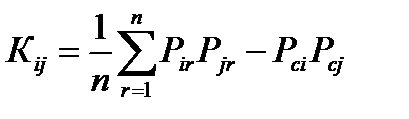, (3.3)

где P c i, P c j – среднее значение (математического ожидания) графиков Pi Pj.

Для качественного анализа взаимной корреляции иногда бывает удобно использовать коэффициент корреляции графиков Pi Pj:

.

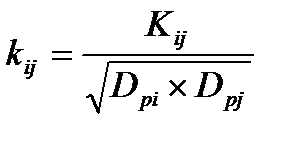ВКМ графиков нагрузки Kij, важен не только с точки зрения оценки взаимосвязи графиков Pi Pj, но он входит в формулу для дисперсии суммар­ного графика P ∑ при суммировании нагрузки N электроприемников, питаю­щихся по одной линии или от одной трансформаторной подстанции.

;

.

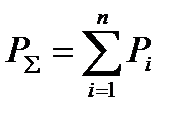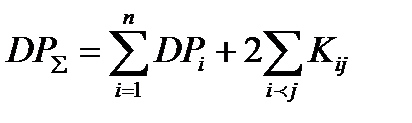В данном случае характеристики графика определяется по одной реа­лизации как для стационарного процесса, обладающего эргодическим свой­ством. Но как это видно из рис.3.1 процессы не являются стационарными. В суточном графике имеются утренний и вечерний максимумы, которые по­вторяются каждые сутки, а также снижение нагрузки в ночные часы. Следо­вательно, имеют место явное невыполнение условий, при которых можно определять характеристики процесса по одной его реализации. С другой сто­роны практика показывает, что характеристики процесса по одной реализа­ции нестационарного суточного графика обладают статистической устойчи­востью, т.е. характеристики, полученные для рабочих суток режимного дня с достаточной для практических расчетов точностью описывают характери­стики и других дней.

На рисунке 3.1 представлены графики получасовых расходов электро­энергии трансформаторных подстанций 10/0,4 кВ городского района, питаю-щих различных потребителей. Графики нагрузки подстанций ТП1-ТП6 име-ют близкие по величине средние значения в диапазоне от 110 кВт до 203 кВт, а график ТП7 отличается меньшей величиной среднего значения Р _С = 30 кВт.

Суточные графики производственных потребителей имеют конфигура-цию, определяемую главным образом типом потребителей и технологичес-ким процессом его работы. Если промышленное производство ориентирова-но на односменную работу, то график имеет, как правило, дневной максимум нагрузок и значительный провал в ночное время (график ТП1 на рис.1).

Графики подстанций, питающих коммунально-бытовые потребители городского района, имеют утренний и более ярко выраженный вечерний мак­симумы (ТП2 - ТП7 на рис.).

Графики ТП1-ТП7 имеют незначительный разброс по коэффициенту заполнения k _ЗАП = Р _С / Р _М = 0,6÷0,8, где Р _С – среднее значение графика; Р _М – максимальное значение. Коэффициенты формы k _Ф, = P _Э/ P _С, характеризую-щие неравномерность графиков, где P Э – эффективное значение суточного графика, изменяются в диапазоне k _Ф = 1,01÷1,05.

Рис. 1 Временные ряды получасовых расходов электроэнергии трансформаторных подстанций 6/0,4 кВ, питающих район города

Для оценки степени различия формы суточных графиков p _{1 i} – p _{7 i} подстанций ТП1-ТП7 используются взаимно-корреляционные моменты (ВКМ) суточных графиков по формуле (3.3).

Значения коэффициентов корреляции, т.е. относительных значений ВКМ определяются следующим образом:

k_ij = 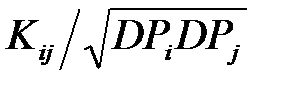, (2)

где K_ij – ВКМ из формулы (1);

DP_i, DP_j – дисперсии графиков нагрузки P_i, P_j, соответственно.

Симметричная матрица коэффициентов взаимной корреляции (2), изображенных на рисунке суточных графиков трансформаторных подстанций ТП1-ТП7, выглядит следующим образом:

К

График ТП1 отличается по форме от графиков остальных ТП так как его максимальные нагрузки приходятся на время с 9 до 15 часов, тогда как у остальных графиков максимальные нагрузки наблюдаются в вечерние часы.

Анализ численных значений коэффициентов взаимной корреляции по­казывает, что график подстанции ТП1 в наименьшей степени коррелирован с графиками остальных подстанций 0,195 ≤ k _{1 j} ≤ 0,592. Коэффициенты вза­имной корреляции графиков нагрузки остальных подстанций положительны и близки к единице 0,888 ≤ k_ij ≤ 0,992.

Дисперсия и ВКМ суточных графиков влияют на величину потерь электроэнергии в сети. Это влияние может быть оценено по значениям дис-персионной и корреляционной составляющих потерь [4]. Увеличение диспер-сии приводит к увеличению потерь; вклад корреляционной составляющей потерь зависит от значений ВКМ в матрице K, которые могут быть как поло­жительными, так и отрицательными.

Задача 3.1.1. Определить среднее значение, дисперсию и среднеквадра­тическое отклонение ступенчатого периодического графика электрической нагрузки, изображенного на рисунке.

Вычислить корреляционные моменты двух графиков нагрузки p ₁(i) и p ₂(i+m) при сдвигах между графиками m = 0, 1, 2,...., 5. В качестве второго графика принять график следующего по номеру варианта.

Построить график корреляционных моментов (корреляционной функ­ции) К (m), m = 0, 1,...., 5. Найти сдвиг m_min, соответствующий минимальному значению корреляционной функции К_min (m_min).

Построить суммарные графики нагрузки P _Σ(i) = p ₁(i) + p ₂(i+m):

а) при сдвиге m = 0, P _Σ1(i) = p ₁(i) + p ₂(i);

б) при сдвиге m_min, P _Σ2(i) = p ₁(i) + p ₂(i+m_min);

Для графиков P _Σ1(i) и P _Σ2(i) вычислить:

а) средние значения P _ΣC1, P _ΣC2 и дисперсии DP _Σ1, DP _Σ2 и найти максимальные значения ординат Р _Σ1max, Р _Σ2max;

б) Коэффициенты заполнения K _З1, K _З2 и коэффициенты формы К _Ф1, К _Ф2.

Сравнить характеристики суммарных графиков Р _Σ1(i) и Р _Σ2(i). Оценить количественно изменения характеристик суммарного графика P _Σ(i) (P _ΣC1, P _ΣC2, DP _Σ1, DP _Σ2 Р _Σ1max, Р _Σ2max., K _З1, K _З2 К _Ф1, К _Ф2) при изменениях сдвига во времени m между графиками p ₁(i), p ₂(i+m) (m = 0, m = m_min)/

Date: 2015-07-01; view: 1335; Нарушение авторских прав