ВВЕДЕНИЕ. Вероятностные методы в электроснабжении

Вероятностные методы в электроснабжении

Учебно-методическое пособие к практическим занятиям и индивидуальным заданиям

Новочеркасск, 2012г

СОДЕРЖАНИЕ

ВВЕДЕНИЕ................................................. 3

СЛУЧАЙНЫЕ ЯВЛЕНИЯ

2. СЛУЧАЙНЫЕ СОБЫТИЯ...................................... 4

2.1 Теоремы сложения и умножения вероятностей.

2.2 Формула полной вероятности и формула Байеса

2.3 Повторение опытов

Случайные величины и их законы распределения

3.1 Законы распределения дискретных случайных величин

3.2 Законы распределения непрерывных случайных величин

3.3 Получение законов распределения по опытным данным.

Критерии согласия

3.4 Элементы линейного регрессионного анализа

Элементы теории случайных процессов

4.1 Случайные графики электрической нагрузки

4.1.1 Случайные процессы. Случайные графики электрической

нагрузки

4.1.2 Суточный график электрической нагрузки как реализация

случайного процесса.

ЛИТЕРАТУРА

ПРИЛОЖЕНИЕ 1Таблица значений функции распределения для нормального закона

ПРИЛОЖЕНИЕ 2 Значения распределения χ² для заданных чисел степеней свободы r и уровней значимости α

ВВЕДЕНИЕ

Изложение теории вероятностей и математической статистики в строго формализованном виде на основе теории меры не в полной мере способствует выработке у изучающих правильных интуитивных понятий, связанных с этими дисциплинами.

Существует своего рода вероятностное мышление или вероятностный взгляд на окружающий действительный мир, которые формируются поэтапно, по мере углубления в эти своеобразные разделы математики.

Математическая статистика — наука, изучающая методы обработки результатов наблюдений массовых случайных явлений, обладающих статистической устойчивостью, закономерностью, с целью выявления этой закономерности. Выводы о закономерностях, которым подчиняются явления, изучаемые методами математической статистики, всегда основываются на ограниченном, выборочном числе наблюдений. При большем числе наблюдений эти выводы могут оказаться иными. Для вынесения более определенного заключения о закономерностях явления математическая статистика опирается на теорию вероятностей.

В отличие от математической статистики, имеющей дело с результатами наблюдений случайных явлений, теория вероятностей формально — логически изучает закономерности случайных явлений и имеет дело с математическими моделями случайных явлений. Обработав результаты наблюдений, исследователь выдвигает ряд гипотез, предположений о том, что рассматриваемое явление можно описать той или иной вероятностной теоретической моделью. Далее, используя математико-статистические методы, можно дать ответ на вопрос, какую из гипотез или моделей следует принять. Именно эта модель и считается закономерностью изучаемого явления. Правомерен такой вывод или нет, покажет практика использования выбранной модели. Таков типичный путь математико-статистического исследования.

Математическая статистика, опираясь на вероятностные модели, в свою очередь, влияет на развитие теории вероятностей. Окружающий нас мир многообразен, и задачи, возникающие при изучении тех или иных случайных явлений, при обработке результатов наблюдений над ними требуют разработки новых вероятностных моделей. Математическая статистика и теория вероятностей — две неразрывно связанные науки.

Самостоятельное решение задач является важным элементом освоения основ теории вероятностей, понимания закономерностей поведения случайных событий, величин, процессов.

Известный специалист по теории вероятностей Мостеллер Ф. в своей книге «Пятьдесят занимательных вероятностных задач с решениями» (М.: Наука, 1971. - 104 с) сказал: «Большей частью своего математического образования, я обязан решению различных задач. С годами мне все труднее становится отделить серьезные занятия от решения, казалось бы, «игрушечных» задач. Очень часто элементарные задачи оказывались чрезвычайно полезными при решении серьезных проблем».

Несколько слов об истории этой математической теории. Назовем несколько наиболее значимых имен из числа создателей теории.

Возникновение теории относится к середине XVII века и было связано с анализом азартных игр: бросание монеты, игра в кости, игра в карты.

I этап (вторая половина XVII века) — возникновение теории — связан с известными именами: Б. Паскаль — французский математик, физик, философ, П. Ферма — французский математик, X. Гюйгенс — французский голландец, математик, механик, Я. Бернулли — швейцарский математик, А. Муавр — английский математик.

II этап (XVIII век — начало XIX века) характеризуется введением аналитических методов, он связан с прикладными задачами артиллерии и задачами измерений. В этот период теорию продвинули П. Лаплас — французский астроном, математик, физик, К. Гаусс — немецкий математик, С. Пуассон — французский математик и механик.

III этап (середина XIX века — начало XX века) — развитие теории. Этап связан в основном с русскими именами: П.Л. Чебышев, А.А. Марков, А.А. Ляпунов, В.Я. Буняковский.

IV современный этап (XX век) связан с наиболее значимыми именами: С.Н. Бернштейн, А.Я. Хинчин, А.Н. Колмогоров, Б.В. Гнеденко (русские математики), Н. Винер, В. Феллер, Крамер (американские математики).

В краткой исторической справке о развитии теории вероятностей данной в [ ] упоминается Б.В. Гнеденко, как внесший вклад в развитие одного из разделов теории вероятностей – теории массового обслуживания.

Следует добавить, что Б.В. Гнеденко проявлял интерес к теории электрических нагрузок и, в частности, к проблеме расчета электрических нагрузок. Им опубликован ряд статей [ ], в которых он совместно с Мешелем С.Б. предложил статистический метод определения электрических нагрузок.

В приложениях вероятностно-статистических методов и теории электрических нагрузок к другим задачам электроснабжения, имеющим вероятностную природу выдающийся вклад принадлежит профессору.М. Каялову, который в конце 60-х годов прошлого века разработал метод расчета электрических нагрузок - метод упорядоченных диаграмм.

В работах Каялова Г.М. были также заложены основы корреляционной теории электрических нагрузок, базирующейся на положениях теории случайных процессов.

В теории электрических нагрузок профессором Г.М. Каяловым была впервые применена однопараметрическая модель 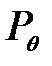(t) осредненного на интервале 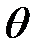процесса P (t):

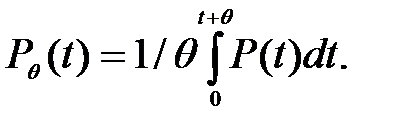
Как указано в [Кур] осреднение процесса P (t) на интервале 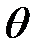эквивалентно пропусканию его через сглаживающий фильтр. Введено понятие кумулятивного процесса k -го порядка, как обобщение понятия осредненного процесса (1.17), а также предложена инерционная модель графика нагрузки P (t), на основе которой разработан инерционный метод расчета электрических нагрузок.

Куренный Э.Г.

Фокин Ю.А.

Жежеленко И.В.

Степанов В.П.

Гордеев В.И. (Надтока И.И.) корреляция

Date: 2015-07-01; view: 1022; Нарушение авторских прав