
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Законы распределения непрерывных случайных величин
|
|
Задача 2.2.1 Значения напряжение на шинах подстанции U 1, U 2,......, Ui,..., Un, измеренные в моменты времени t 1, t 2,..., ti,..., tn (ti +1 - ti = ∆ t = const) – есть значения случайной величины, распределенной по нормальному закону с математическим ожиданием М [ U ] = U c и среднеквадратическим отклонением σ[ U ]. (Принято, что напряжение в сети U (t) – стационарный эргодический процесс). Определить вероятность того, что случайная величина U в момент времени t примет значение в диапазоне от 0,95 U н до 1,05 U н, т.е. не выйдет за пределы ±5% U н. Построить графики функции распределения и функции плотности вероятности случайной величины U.
Таблица 4
| № вар. | U н кВ | U c = M [ u ] кВ | σ [ u ] кВ | № вар | U н, кВ | U c = M [ u ] кВ | σ [ u ] кВ |
| 10,3 | 0,2 | 9,8 | 0,3 | ||||
| 10,2 | 0,15 | 9,7 | 0,25 | ||||
| 9,9 | 0,30 | 0,5 | |||||
| 6,1 | 0,1 | 0,6 | |||||
| 6,2 | 0,08 | 0,7 | |||||
| 5,95 | 0,15 | 10,4 | 0,25 | ||||
| 35,7 | 0,5 | 10,25 | 0,3 | ||||
| 0,6 | 10,3 | 0,25 | |||||
| 34,5 | 0,7 | 5,9 | 0,1 | ||||
| 34,8 | 0,8 | 6,1 | 0,09 | ||||
| 10,4 | 0,25 | 6,15 | 0,1 | ||||
| 9,9 | 0,4 | 9,9 | 0,35 | ||||
| 10,5 | 0,24 |
2.3 Приближенная оценка среднеквадратического отклонения для нормального закона распределения. Правило «трех сигм».
Знание математического ожидания mх и среднеквадратического отклонения σх случайной величины Х позволяет приближенно указать диапазон ее практически возможных значений. Для нормального закона распределения Р (mх- 3 σх < х < mх+ 3 σх) = 0,9973 (см. рис.). Следовательно, с вероятностью 0,9973 можно утверждать, что наблюдаемые значения случайной величины будут находиться в интервале (mх- 3 σх ; mх+ 3 σх).
Такой способ оценки диапазона возможных значений случайной величины в прикладной статистике называются правилом «трех сигма». Из этого правила вытекает ориентировочный способ оценки среднеквадратического отклонения случайной величины: определяют максимальное практически возможное отклонение от среднего и делят его на три или определяют минимальное и максимальное значение и интервал между ними делят на шесть.
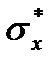 = (xmax – xmin)/6
= (xmax – xmin)/6
Разумеется, что такой приближенный способ может использоваться только если известно, что случайная величина Х имеет нормальный закон распределения и нет других более точных способов определения σх.
Пример решения типовой задачи. Известно, что значения напряжения в розетках квартиры 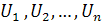 измеренные в моменты времени
измеренные в моменты времени  – это значения непрерывной случайной величины, распределенной по нормальному закону с математическим ожиданием
– это значения непрерывной случайной величины, распределенной по нормальному закону с математическим ожиданием 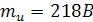 и среднеквадратическим отклонением
и среднеквадратическим отклонением 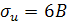 . Определить вероятность того, что напряжение в сети в момент времени
. Определить вероятность того, что напряжение в сети в момент времени 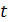 не выйдет за пределы
не выйдет за пределы 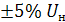 . Номинальное напряжение в сети
. Номинальное напряжение в сети 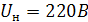 .
.
Построить график функции плотности вероятностей 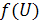 случайной величины
случайной величины 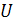 и график функции распределения
и график функции распределения 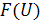 .
.
Функция плотности вероятностей случайной величины 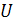 , распределенной по нормальному закону с параметрами
, распределенной по нормальному закону с параметрами 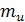 и
и 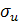 имеет вид:
имеет вид:
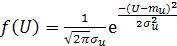 .
.
Для приблизительного построения графика функции 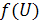 можно воспользоваться правилом «трех сигм» и вычислить несколько значений функций на интервале от
можно воспользоваться правилом «трех сигм» и вычислить несколько значений функций на интервале от 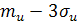 до
до 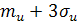 , т.е. на интервале от
, т.е. на интервале от 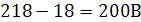 до 218+18=236B.
до 218+18=236B.
Примем в качестве начальной и конечной точек для построения 203В и 233В и вычислим значения функции 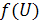 в точках 203В, 205В,… 233В, т.е. с шагом равным 0,5
в точках 203В, 205В,… 233В, т.е. с шагом равным 0,5 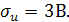
Таблица 2.1.
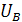
| |||||||||||||
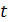
| -3 | -2,5 | -2 | -1,5 | -1,0 | -0,5 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | ||
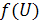
| 0,0007 | 0,003 | 0,009 | 0,022 | 0,040 | 0,059 | 0,0665 | 0,059 | 0,040 | 0,022 | 0,009 | 0,003 | 0,0007 |
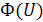
| 0,499 | 0,494 | 0,477 | 0,433 | 0,341 | 0,191 | 0,00 | 0,191 | 0,341 | 0,433 | 0,477 | 0,494 | 0,499 |
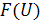
| 0,001 | 0,006 | 0,023 | 0,067 | 0,159 | 0,309 | 0,5 | 0,691 | 0,841 | 0,933 | 0,977 | 0,994 | 0,999 |
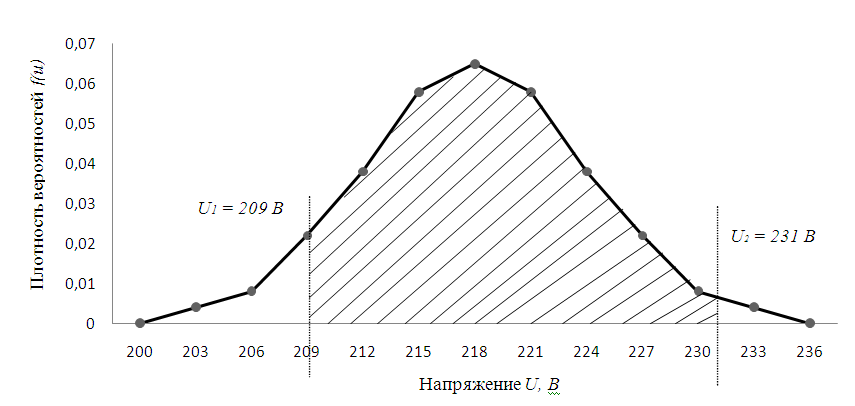
График функции плотности вероятностей 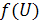 показан на рис. 2.1.
показан на рис. 2.1.
Определим также значения функции распределения
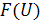 в этих же точках. Для удобства вычисления функции
в этих же точках. Для удобства вычисления функции
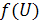 по формуле (), а также для определения значений функции
по формуле (), а также для определения значений функции
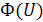 из таблицы 1 приложения вычислим значения безразмерного параметра
из таблицы 1 приложения вычислим значения безразмерного параметра 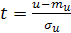 .
.
Значения 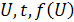 и
и 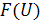 приведены в таблице 3.
приведены в таблице 3.
Для 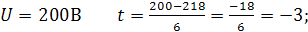
Для 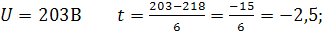
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Для 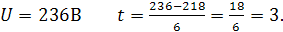
Значения 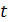 приведены в таблице 3.
приведены в таблице 3.
По значениям параметра 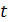 в таблице 1 Приложения находим значения функции
в таблице 1 Приложения находим значения функции 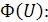
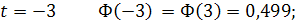
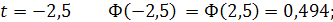 и т.д.
и т.д.
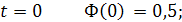
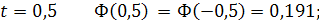
Значения функции 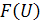 определяется по значениям функции
определяется по значениям функции  следующим образом:
следующим образом:
а) при отрицательных значениях
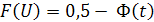
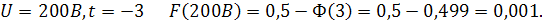
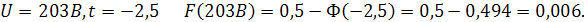
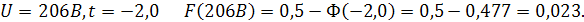
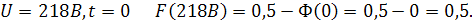
б) при положительных значениях t
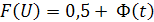
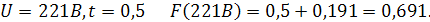
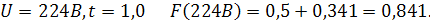
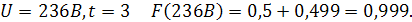
График функции 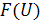 показан на рис. 2.2.
показан на рис. 2.2.
Для определения вероятности того, что напряжение в сети не выйдет за пределы 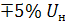 необходимо определить граничные значения диапазона:
необходимо определить граничные значения диапазона:
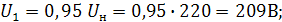
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 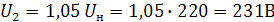
Далее необходимо привести границы интервала 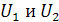 и безразмерным величинам
и безразмерным величинам 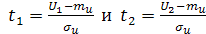 , т.е. к границам диапазона безразмерной случайной величины t, распределенной по нормальному
, т.е. к границам диапазона безразмерной случайной величины t, распределенной по нормальному 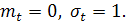
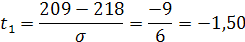
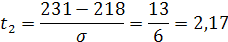
Значения функции распределения вида:
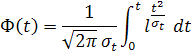
Приведены в таблице1 приложения. Значения функции  для точек
для точек 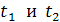 равны:
равны: 
Вероятность того, что случайная величина напряжения в сети не выйдет за пределы 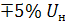 определяется следующим образом:
определяется следующим образом:
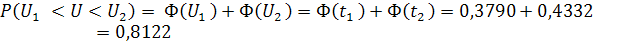
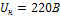
|
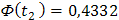
|
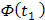 =0,3790 =0,3790
|
Задача 2.2.2 Длительность простоев дуговой сталеплавильной печи t пр распределена по экспоненциальному закону с параметром l. Определить вероятность того, что:
а) простой печи составит менее b часов и более a часов P (a < t пр < b);
б) простой печи превысит b часов P (t пр > b).
Значения a, b, l заданы в таблице 4.
Таблица 4
| № вар. | λ [1/час] | а [час] | B [час] | № вар. | λ [1/час] | а [час] | б [час] |
| 0,5 | 0,8 | 0,6 | 0,5 | 1,5 | |||
| 0,5 | 0,9 | 1,5 | 0,6 | 0,8 | 1,8 | ||
| 0,5 | 0,9 | 1,7 | 0,6 | 0,9 | 2,2 | ||
| 0,5 | 1,5 | 0,6 | 0,8 | 2,0 | |||
| 0,4 | 0,7 | 2,0 | 0,8 | 0,5 | 2,5 | ||
| 0,4 | 1,2 | 2,2 | 0,8 | 0,5 | 2,0 | ||
| 0,4 | 1,0 | 0,8 | 0,8 | 2,5 | |||
| 0,4 | 1,2 | 2,5 | 0,8 | 1,0 | 2,0 | ||
| 0,25 | 1,0 | 0,5 | 2,5 | ||||
| 0,25 | 0,9 | 2,5 | 1,0 | 0,5 | 2,0 | ||
| 0,25 | 2,2 | 1,0 | 0,4 | 2,2 | |||
| 0,25 | 2,5 | 1,0 | 0,3 | 1,5 | |||
| 0,9 | 0,4 | 1,8 |
Date: 2015-07-01; view: 699; Нарушение авторских прав