
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоремы сложения и умножения вероятностей
|
|
Полная группа событий. Если в результате опытов обязательно должно появиться хотя бы одно из нескольких событий, то эти события образуют полную группу событий.
Примеры событий образующих полную группу:
а) появление герба или появление цифры при бросании монеты;
б) электроприемник включен или электроприемник выключен в момент времени t;
в) к силовому шкафу подключены четыре электроприемника. Отключены все четыре электроприемника, включен один, включено два, включено три, включены все четыре электроприемника;
г) ток в кабеле превышает допустимое значение по нагреву и ток в кабеле не превышает допустимое значение.
Несовместные события. Несколько событий называются несовместными, если никакие два или более из них не могут появиться вместе.
Примеры несовместных событий:
а) выпадение герба и цифры при бросании монеты;
б) включенный электроприемник и отключенный электроприемник;
в) один отказ, два отказа, три отказа релейной защиты за один год работы.
Равновозможные события:
а) выпадение герба и выпадение цифры при бросании монеты. Р =0,5.
б) появление цифр 1,2,3,4,5,6 при бросании игрального кубика. 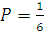 .
.
в) вероятность вытащить на экзамене экзаменационный билет №1 (№ 2, № 3, … № 25) из 25. 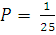 .
.
Сумма и произведение событий. Суммой двух событий А и В называется событие С состоящее в выполнении либо события А либо события В или обоих вместе.
Суммой нескольких событий А 1, А 2,,… Аn называется событие С, состоящее в появлении хотя бы одного из них: С = А 1 + А 2 +…+ Аn
Произведением двух событий А, В называется такое событие D, состоящее в совместном появлении и события А и события В:
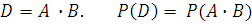 .
.
Произведением нескольких событий А 1, А 2,,… Ап называется событие D, состоящее в совместном появлении всех этих событий: D = А 1, А 2 … Аn
Формулы сложения вероятностей.
Вид формулы сложения вероятностей зависит от того, являются суммируемые события совместными или несовместными.
Вероятность суммы двух несовместных событий А, В равна сумме вероятностей этих событий.
Р (А + В) = Р (А) + Р (В) (1)
Для любого числа несовместных событий А 1, А 2,,… Аn формула (1) выглядит следующим образом

Если события А 1, А 2,,… Аn образуют полную группу, то сумма их вероятностей равна единице
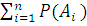 = 1.
= 1.
Вероятность суммы двух совместных событий А, В определяется по формуле
Р (А + В) = Р (А) + Р (В) – Р (А 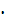 В),
В),
где Р (А 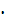 В) – вероятность произведения событий А, В.
В) – вероятность произведения событий А, В.
Для суммы трех совместных событий А, В, С формула сложения вероятностей имеет следующий вид:
Р (А+В+С) = Р (А) + Р (В)+ Р (С)- Р (АВ)- Р (АС)- Р (ВС)+ Р (АВС),
где Р (АВС) – вероятность произведения событий А, В, С.
Для суммы четырех совместных событий А, В, С, D:
Р (А + В + С + D) = Р (А) + Р (В) + Р (С) + Р (D) - Р (АВ) - Р (АС) - Р (А D) –
- Р (ВС) – Р (ВD) - Р (С D) + Р (АВС) + Р (АВD) + Р (АСD) + Р (ВСD) - Р (АВС D).
В общем виде формула для сложения вероятностей событий А 1, А 2, А 3,… Аn имеет вид:
Р 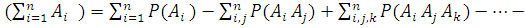
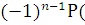 А 1, А 2, … Аn).
А 1, А 2, … Аn).
Формулы умножения вероятностей.
Вид формул умножения вероятностей для событий зависит от того являются ли рассматриваемые события зависимыми или независимыми.
Независимые события. Независимыми называются такие события, что появление одного из них не влияет на вероятность появления другого. Если два события А,В являются независимыми, то вероятность того, что появится и событие А и событие В, т.е. появится событие АВ определяется как произведение вероятностей событий: Р(АВ) = Р (А) Р (В).
Для нескольких независимых событий А 1, А 2 …, Аn вероятность того, что появится и событие А 1 и событие А 2, … и событие Аn определяется как произведение вероятностей событий:
Р (А1, А 2 …, Аn) = 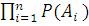 = Р (А 1 ) Р (А 2)… Р (А n).
= Р (А 1 ) Р (А 2)… Р (А n).
Зависимые события. Зависимыми называются такие события, что появление одного из них влияет на вероятность появления другого. Для двух зависимых событий А,В вероятность того что появится и событие А и событие В, т.е. появится событие АВ определяется по формуле:
Р (АВ) = Р (А) Р (В|А) = Р (В) Р (А|В),
где Р (В|А), Р (А|В) – условные вероятности: Р (А|В) – вероятность появления события А при условии что произошло событие В; Р (В|А) – вероятность появления события В при условии, что появилось событие А.
Для трех зависимых событий А,В,С вероятность произведения определятся следующим образом:
Р (АВС) = Р (А) Р (В|А) Р (С|АВ) = Р (В) Р (А|В) Р (С|АВ) = Р (С) Р (А|С) Р (В|АС)
Вероятность произведения n зависимых событий А1, А2 …, Аn определяется по формуле:
Р (А1, А2 …, Аn) = Р (А1) Р (А2 |А1) Р (А3 | А1 А2 )… Р (Аn | А1 А2 … Аn-1 ).
Задача 1.1 Электрическая цепь между точками А и В составлена по схеме, приведенной на рис. 1.1-1.20. Вероятность безотказной работы за время Т различных элементов - независимые события, имеющие вероятности, приведенные в таблице.
Найти вероятности:
а) безотказной работы (отсутствие разрыва цепи между точками А, В) за время Т;
б) разрыва цепи за время Т.
Таблица 1 Вероятности безотказной работы элементов за время Т
| Вариант задания | Элемент цепи | ||||
| Л1 | Л2 | К1 | К2 | К3 | |
| 0,9 | 0,85 | 0,7 | 0,8 | 0,95 | |
| 0,8 | 0,6 | 0,9 | 0,75 | 0,85 | |
| 0,7 | 0,75 | 0,8 | 0,55 | 0,8 | |
| 0,85 | 0,7 | 0,75 | 0,6 | 0,9 | |
| 0,6 | 0,9 | 0,7 | 0,8 | 0,75 | |
| 0,75 | 0,8 | 0,65 | 0,85 | 0,7 | |
| 0,65 | 0,85 | 0,85 | 0,7 | 0,55 | |
| 0,8 | 0,7 | 0,55 | 0,9 | 0,85 | |
| 0,7 | 0,85 | 0,6 | 0,8 | 0,65 | |
| 0,9 | 0,6 | 0,7 | 0,85 | 0,75 |
Пример решения задачи. Пусть дана электрическая цепь, приведенная на рисунке, состоящая из трех последовательно-параллельно соединенных лампочек 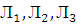 . Вероятности безотказной работы (отсутствие разрыва) в момент времени t работы соответственно: p 1 = 0,7; p 2 = 0,8; p 3 = 0,9. Определить вероятность отсутствия разрыва цепи на участке L, M, N за время T.
. Вероятности безотказной работы (отсутствие разрыва) в момент времени t работы соответственно: p 1 = 0,7; p 2 = 0,8; p 3 = 0,9. Определить вероятность отсутствия разрыва цепи на участке L, M, N за время T.
| L |
| Л1 |
| М |
| N |
| Л2 |
| Л3 |
Рис.1
Данная задача может быть решена двумя способами: а) с применением формул сложения и умножения вероятностей событий; б) комбинаторным способом.
Решение задачи с помощью формул сложения и умножения вероятностей событий.
Рассмотрим следующие события:
Л1 – первая лампочка исправна P (Л1) = p 1 ;
Л2 – вторая лампочка исправна P (Л2) = p 2 ;
Л3 – третья лампочка исправна P (Л3) = p 3.
Определим вероятность события А – отсутствия разрыва цепи на участке MN (параллельное соединение лампочек 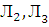 ).
).
Отсутствие разрыва цепи на этом участке может быть в том случае если не перегорели либо лампочка 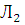 с вероятностью P (Л2) = p 2, либо лампочка
с вероятностью P (Л2) = p 2, либо лампочка 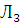 c вероятностью P (Л3) = p 3, либо обе лампочки
c вероятностью P (Л3) = p 3, либо обе лампочки 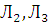 не перегорели.
не перегорели.
Следовательно, вероятность отсутствия разрыва цепи на участке MN равна сумме вероятностей событий Л2 и Л3: А = Л2 + Л3 , P (A) = P (Л2 + Л3)
P (A) = P (Л2 + Л3)= P (Л1) + P (Л2) - P (Л2 Л3)
События Л2 и Л3 - совместные.
P (A)= p2 + p3 - p2 p3 = 0,8 + 0,9 - 0,8 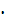 0,9 = 1,7 – 0,72 = 0,98
0,9 = 1,7 – 0,72 = 0,98
Обратите внимание: вероятность отсутствия разрыва цепи (безотказной работы) при параллельном соединении больше чем наибольшая из вероятностей отдельных элементов. Р (А) 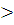 Р (
Р (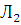 ), Р (А)
), Р (А) 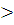 Р (
Р (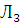 ).
).
После вычисления вероятности события А схему можно привести к следующему виду:
| L |
| Л1 |
| А |
| N |
Рис. 2
Определим вероятность события В – отсутствие разрыва цепи на участке L N (последовательное соединение лампы Л 1 c элементом А):
Разрыва цепи на участке L,N не будет если произойдут оба события: событие Л1 с вероятностью P (Л1) = p 1 и событие А с вероятностью Р (А), т.е. В = Л1 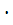 А, а P (В) = P (Л1)
А, а P (В) = P (Л1) 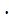 P (А)= p 1
P (А)= p 1 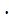 P (A)= p 1 (p 2 + p 3 - p 2 p 3), откуда
P (A)= p 1 (p 2 + p 3 - p 2 p 3), откуда
P (В)=0,7 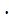 0.98 = 0,686.
0.98 = 0,686.
Вероятность отсутствия разрыва цепи (надежность) при последовательном соединении элементов меньше вероятности события с наименьшей вероятностью: P (В) 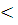 P (Л1); P (В)
P (Л1); P (В) 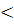 P (A)
P (A)
Комбинаторный способ решения данной задачи заключается в следующем. Вероятность отсутствия разрыва цепи на участке L N определяется как сумма вероятностей таких комбинаций состояния элементов цепи Л1, Л2, Л3, при которых не будет разрыва цепи. В рассматриваемом случае такими комбинациями являются следующие (несовместные события): Л1, Л2, Л3, Л1, Л2, 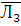 , Л1,
, Л1, 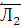 , Л3, где
, Л3, где 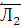 и
и 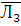 -события противоположные событиям Л2 и Л3, т.е. отказы элементов.
-события противоположные событиям Л2 и Л3, т.е. отказы элементов.
Вероятность события В равна сумме вероятностей:
P (В)= p 1 p 2 p 3 + p 1 p 2 q 3 + p 1 q 2 p 3,
где qi =1 – рi вероятности обратного события из соотношения pi + qi =1.
После несложных преобразований получим выражения тождественное полученному ранее:
P (В)= p 1(p 2 p 3 + p 2 q 3 + q 2 p 3) = p 1[p2(p 3 + q3) + q 2 p 3] = p 1(p 2+ q 2 p 3) = p 1[(p2 + (1- p 2 )p3] = p 1[p2+ p 3 – p 2 p 3].
Date: 2015-07-01; view: 918; Нарушение авторских прав