Функции алгебры логики

Закодируем состояния каждого из элементов структурной схемы двоичными переменными: 1 (элемент исправный), 0 (элемент в отказовом состоянии).

Тогда функционирование системы можно описать с помощью функций алгебры логики (ФАЛ), используя операции конъюнкции, дизъюнкции и инверсии. В качестве примера составим ФАЛ, соответствующую работоспособности системы с последовательным соединением элементов. Система находится в работоспособном состоянии при условии, что все ее элементы исправны. Обозначим х_i — исправное состояние i -го элемента, — отказовое состояние, i = 1,2,..., п. Тогда ФАЛ будет иметь вид:

Приведем еще один пример. Структурная схема системы имеет вид, представленный на рис. 5.2.

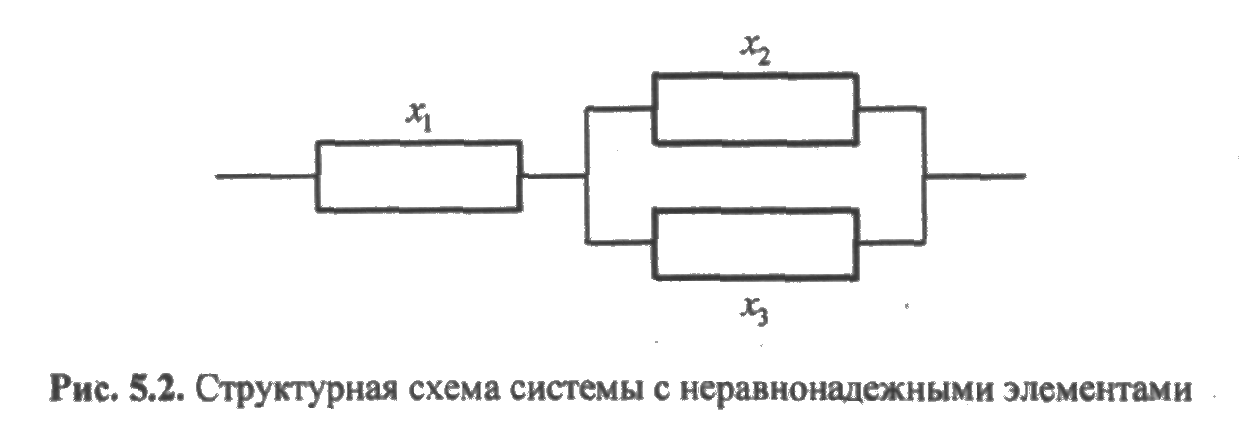
Система будет в работоспособном состоянии в следующих случаях: все элементы исправны, исправными являются элементы 1 и 2 или 1 и 3. Тогда ФАЛ, соответствующая функции работоспособности, будет иметь вид:

Процедура получения ФАЛ может быть формализована. Одним из способов формализации является получение совершенной дизъюнктивной нормальной формы (СДНФ), получаемой из таблицы истинности, соответствующей работоспособному состоянию системы.

Пусть, например, структурная схема системы имеет вид, показанный на рис. 5.3.

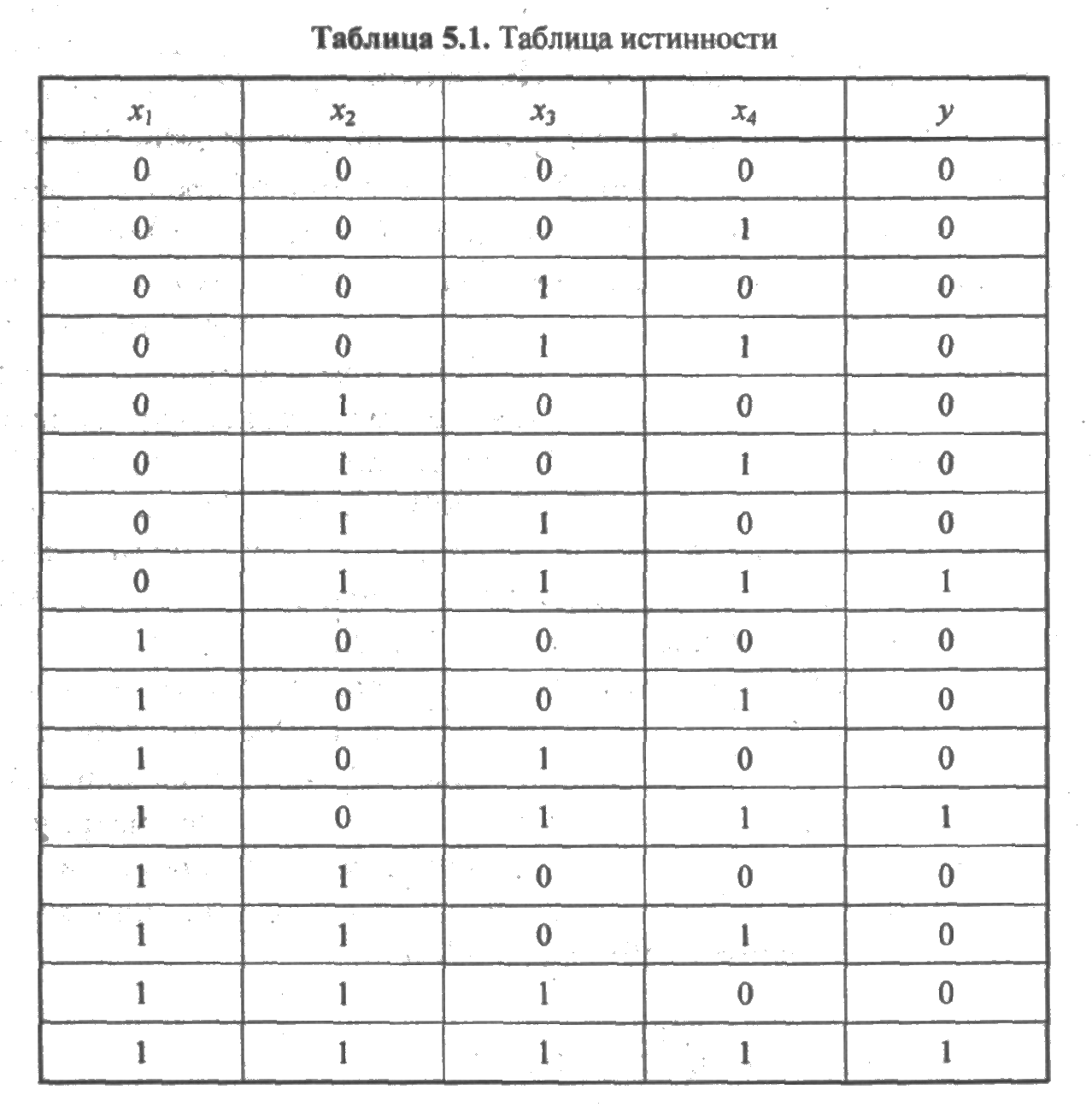
Функция у(х₁,х₂,х₃,х₄) имеет значение 1 лишь на трех наборах двоичных аргументов:

- 0111 (исправными являются элементы х₂,х₃,х₄);

- 1011 (исправнымиявляются элементы х₁,х₃,х₄);

- 1111 (все элементы исправны).

Тогда следующая СДНФ будет функцией алгебры логики, описывающей работоспособное состояние системы:

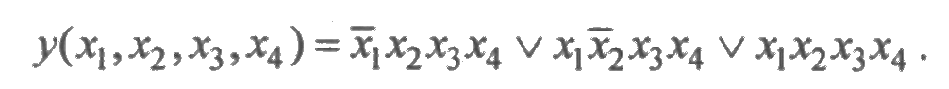
Функция алгебры логики может быть математической моделью функционирования системы в смысле ее надежности.

Способы получения ФАЛ, достоинства и недостатки метода более подробно описаны в разд. 5.3.

5.1.3. Матрица состояний системы

В матрице состояний содержится вся информация о функционировании системы в смысле ее надежности. Каждая строка матрицы представляет собой вектор, компонентами которого служат признаки о том, в каком состоянии пребывает каждый элемент, когда сама система находится в состоянии i ' i ϵ Е, где Е — множество всех состояний системы. Элемент может находиться не только в двух состояниях: работает или восстанавливается. Элемент системы может находиться в состоянии простоя, которое вызвано различными причинами. Для дальнейшей работы системы необходимо знание того, вызван ли указанный простой элемента очередью на. восстановление или отказом других элементов, или элемент является резервным и находится в ненагруженном состоянии и т. д. Задание матрицы состояний системы было подробно описано в гл. 4. Вместо матрицы состояний информация о функционировании системы может находиться в аргументах функций, являющихся неизвестными в системе интегральных уравнений. Достоинством описания системы с помощью матрицы состояний является удобство ее хранения в памяти ЭВМ или на внешнем носителе информации. При этом матрица может иметь практически любую размерность. Другое дело — использование этой матрицы для построения системы интегральных уравнений. Данный вопрос достаточно сложный и требует серьезного изучения.

5.1.4. Граф состояний системы

Восстанавливаемая система, состоящая из п элементов, может находиться в большом числе состояний. Например, i -е устройство отказало (i = 1, 2,..., n), а остальные исправны; i -е и j -е устройства отказали, а остальные исправны, и т. д. Из-за отказов и восстановлений система в дискретные моменты времени переходит из одного состояния в другое. В процессе длительной эксплуатации она может побывать в каждом из возможных состояний многократно. Тогда ее функционирование может быть описано графом, узлам которого приписываются состояния системы, а ветвям — возможные переходы из состояния в состояние. Если в графе имеется n узлов, то среди них будет k узлов, соответствующих отказовым состояниям, и (п-k) — исправным.

Если оценивать функционирование системы до некоторого i -го состояния, например до первого ее отказа, то i -е состояние считается поглощающим. Система, попавшая в i -е состояние, уже не может перейти в другое, и в графе отсутствуют ветви переходов из этого состояния (говорят, что в такие ветви ставится экран).

Вид графа зависит от структуры системы (схемы расчета надежности), числа обслуживающих бригад и дисциплины обслуживания. Обычно узлы графа нумеруются и отмечаются (например, крестом) те, которые соответствуют отказовым состояниям системы. На графе также указываются все интенсивности переходов.

Рассмотрим примеры графов, описывающих функционирование системы в смысле ее надежности.

ПРИМЕР 5.1. Схема расчета надежности нерезервированной системы приведена на рис. 5.4, где приняты обозначения:

- п — число элементов системы;

- λ_i — интенсивность отказа i -го элемента;

- μ _i, — интенсивность восстановления i -го элемента, i = 1, 2,..., п.

Граф состояний рассматриваемой нерезервированной восстанавливаемой системы приведен на рис. 5.5.

Исправное состояние обозначено (0), а отказовые пронумерованы от 1 до n и изображены квадратами. В любом i -м отказовом состоянии система не работает, а i -й элемент находится в ремонте. Очевидно, что система в i -е отказовое состояние может попасть с интенсивностью отказа i -го элемента, т. е. λ_i, и может быть восстановлена (возвращена в состояние (0)) с интенсив­ностью μ_i,.

Указанные интенсивности приведены на графе. В рассматриваемом случае вид графа и интенсивности переходов не зависят от числа обслуживающих бригад, т. к. предполагается, что после возникновения отказа одного элемента вся система не работает и отказы элементов в процессе ее восстанбвления не возникают.

Если необходимо проанализировать поведение системы до первого отказа, то следует считать, что состояния (1), (2),..., (n) являются поглощающими (система, попав в эти состояния, больше не возвращается в исправное состояние (0), экран на графе состояний).

ПРИМЕР 5.2. Необходимо описать графом функционирование дублированной системы, схема расчета надежности которой приведена на рис. 5.6.

Рассмотреть следующие случаи:

а) систему обслуживают две бригады;

б) обслуживание осуществляется одной бригадой с прямым приоритетом;

в) обслуживание осуществляется одной бригадой с обратным приоритетом;

г) обслуживание осуществляется одной бригадой, причем первый элемент имеет высший приоритет по сравнению со вторым.

Решение. Из рис. 5.6 видно, что дублированные устройства неравнонадежны и обладают различной ремонтопригодностью. Предполагается также, что последействие отказов отсутствует.

Графы состояний системы для всех случаев приведены на рис. 5.7.

Cистема может находиться в следующих состояниях:

- (0) — состояние, когда оба устройства исправны;

- (1) — состояние, когда первое устройство отказало и находится в ремонте, а второе исправно;

- (2) — состояние, когда второе устройство отказало и находится в ремонте, а первое исправно;

- (3) — отказовое состояние системы, когда оба устройства неисправны; при этом в случае (a) ремонтируются и первое, и второе устройства; в случае (б) и (г) ремонтируется первое, а второе находится в очереди на ремонт, в случае (в) ремонтируется второе, а первое находится в очереди;

- (4) — отказовое состояние, когда оба устройства неисправны, при этом в случае (б) ремонтируется второе устройство, а в случаях (в) и (г)— первое.

Рассмотрим первоначально случай (а) (рис. 5.7, а). В дублированной системе может отказать либо первое, либо второе устройство. Поэтому из исходного состояния (0) возможны два перехода: в состояние (1) с интенсивностью λ₁, ив состояние (2) с интенсивностью λ₂. Отказавшее устройство может быть восстановлено до отказа системы, т. е. система из состояний (1) и (2) может возвратиться в исходное нулевое состояние. Может также оказаться, что до восстановления отказавшего устройства откажет еще одно, и система перейдет в отказовое состояние (3), показанное на графе квадратом. В это состояние она может попасть либо из состояния (1) с интенсивностью λ ₂ (второе устройство отказало), либо из состояния (2) с интенсивностью λ₁ (первое устройство отказало). Так как восстановлением системы занимаются две обслуживающие бригады, то в состоянии (3) оба устройства ремонтируются независимо от того, какое из них отказало первым. Если в состоянии (3) первоначально будет отремонтировано первое устройство, то система перейдет с интенсивностью μ₁, в состояние (2), а если второе — то с интенсивностью μ ₂ в состояние (1).

Случаи (б), (в), (г) отличаются от рассмотренного тем, что ремонтом дублированной системы занимается лишь одна обслуживающая бригада. При таком обслуживании в отказовом состоянии дублированной системы ремонтируется только одно из отказавших устройств, а второе находится в очереди на ремонт. А это значит, что дублированная восстанавливаемая система имеет два разных отказовых состояния, которые объединить в одно в общем случае невозможно. На рис. 5.7, б — г эти состояния обозначены (3) и (4) и показаны квадратами.

При обслуживании дублированной системы с прямым, приоритетом (случай (б)) в отказовом состоянии (3) ремонтируется первое устройство, а в состоянии (4) — второе. Если будет отремонтировано первое устройство, то система перейдет в исправное состояние, когда первое устройство работает, а второе находится в ремонте, т. е. в состояние (2). Интенсивность перехода будет равна интенсивности восстановления μ₁ первого устройства. Если будет отремонтировано второе устройство, то система перейдет в исправное состояние, когда второе устройство работает, а первое находится в ремонте, т. е. в состояние (1). Интенсивность перехода будет равна интенсивности восстановления μ₂ второго устройства.

При обслуживании системы с обратным приоритетом (случай (в)) в состоянии (3) ремонтируется второе устройство, а в состоянии (4) — первое, поэтому из отказовых состояний (3) и (4) возможны переходы соответственно в состояние (1) с интенсивностью μ ₂ и в состояние (2) с интенсивностью μ₁.

В случае (г) первое устройство имеет приоритет в обслуживании, поэтому в отказовых состояниях (3) и (4) оно ремонтируется первым. А это означает что переход системы из отказовых состояний (3) и (4) возможен лишь в исправное состояние (2), когда первое устройство работает, а второе находится в ремонте. Интенсивность перехода равна интенсивности восстановления μ₁ первого устройства.

Из примера следует, что вид графа зависит не только от структуры системы, но также от числа обслуживающих бригад и дисциплины обслуживания.'

Из приведенных примеров видно, что граф состояний восстанавливаемой системы полностью определяется ее структурой (схемой расчета надежности), надежностью устройств, их ремонтопригодностью, числом ремонтных бригад, дисциплиной обслуживания и видом восстановления. В нем содержится вся информация о функционировании системы. Поэтому граф состояний можно рассматривать как один из способов описания поведения системы в смысле ее надежности. Основным преимуществом такого описания является наглядность и сравнительная простота.

Граф состояний сложной системы может иметь большое число узлов. В этом случае при построении графа приходится просматривать большое число возможных сочетаний отказавших элементов. Это можно выполнить при условии формализации построения графа.

5.1.5. Формализованный способ построения графа состояний системы

Каждому узлу графа соответствует определенное состояние системы. Совокупность состояний, когда в системе отказало i устройств, будем называть i -м уровнем графа. Тогда при i =0 (нулевой уровень) все устройства исправны, при i = 1 (первый уровень) одно любое устройство отказало, а остальные исправны, при i = 2 (второй уровень) два любых устройства отказали, а ос­тальные исправны, и т. д.

Исходными данными по построению графа являются: структурная схема системы, интенсивности отказов и восстановления, дисциплина обслуживания, вид восстановления. Для удобства построения графа целесообразно элементы структурной схемы нумеровать и указывать значения их интенсивностей отказов и восстановления.

Сущность формализованного способа построения графа состояний системы заключается в следующем.

Проводятся горизонтальные линии, которым присваиваются номера 0,1, 2,... Линия с номером i соответствует i -му уровню графа. Их целесообразно раcполагать в последовательности возрастания номеров. Первой из них присваивается номер 0 (нулевой уровень системы).

Далее строится граф состояний с переходами от верхних к нижним уровням. Назовем их λ -переходами. Для этого на нулевой горизонтальной линии отмечается точкой или кружком нулевой узел графа, соответствующий состоянию системы, когда все устройства исправны. Затем на линии с номером 1 обозначаются все узлы, соответствующие первому уровню графа. Число узлов первого уровня всегда равно числу устройств (элементов) структурной схемы. Соединяя узел нулевого уровня со всеми узлами первого уровня и отмечая стрелками направление переходов, получим неполный граф состояний системы, который назовем графом первого уровня с λ -переходами. Все узлы первого уровня нумеруются в соответствии с номерами элементов (уст­ройств) структурной схемы, а возле ветвей записываются соответствующие интенсивности переходов. Все узлы первого уровня, которые соответствуют отказовым состояниям системы, необходимо отметить (например, квадратом или крестом). Из этих узлов λ -переходы в узлы более высокого уровня графа отсутствуют.

Для построения графа состояний второго уровня с λ -переходами на линии с номером 2 наносятся узлы графа, соответствующие всем возможным состояниям системы, когда отказали два ее устройства. Все узлы нумеруются двухразрядными числами. Двухразрядное число показывает номера отказавших элементов структурной схемы и последовательность их отказов. Например, если узел второго уровня имеет номер 31, то это значит, что в данном состоянии система оказалась в результате отказа первого и третьего элементов структурной схемы, причем первым отказал третий элемент, а вторым — первый. Соединяя ветвями соответствующие узлы первого и второго уровня и отмечая стрелками направления переходов, получим граф состояний системы, который называется графом второго уровня с λ -переходами.

Узлы, соответствующие отказовым состояниям системы отмечаются квадратами или крестами. Из этих узлов переходы в узлы более высокого уровня отсутствуют. Возле ветвей графа записываются соответствующие интенсивности переходов.

Построение графа состояний с λ -переходами заканчивается тогда, когда все узлы в данном уровне будут соответствовать отказовым состояниям системы.

ПРИМЕР 5.3. Необходимо построить граф состояний системы, схема расчета надежности которой приведена на рис. 5.8. Предполагается, что восстановление неограниченно, последействие отказов элементов отсутствует, а элемент 5 находится в ненагруженном резерве и до отказа элемента 4 его интенсивность отказа равна нулю.

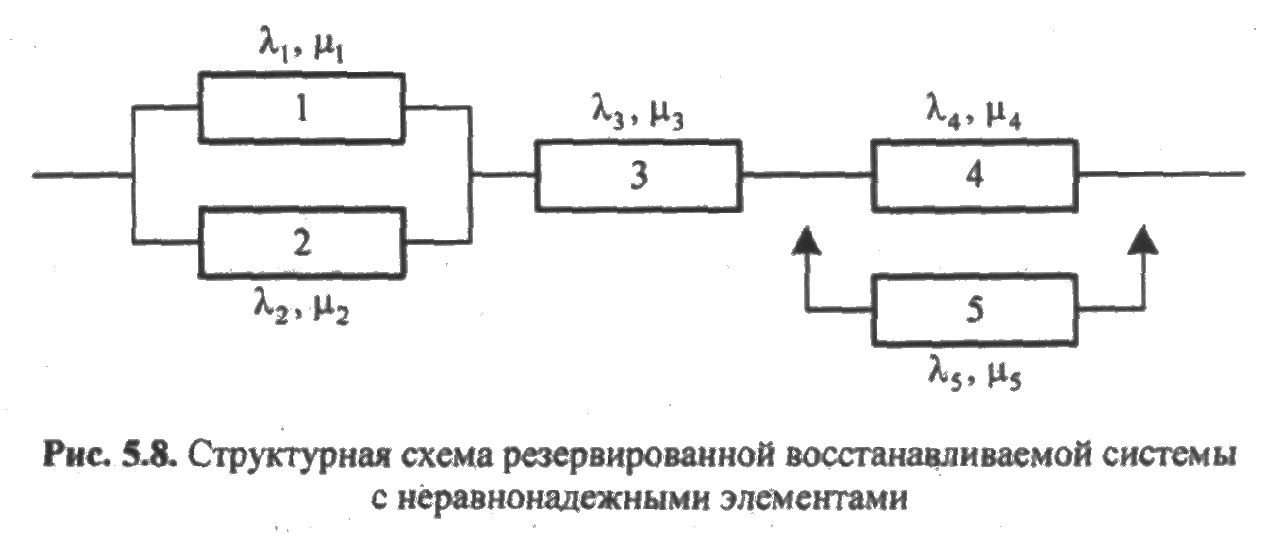
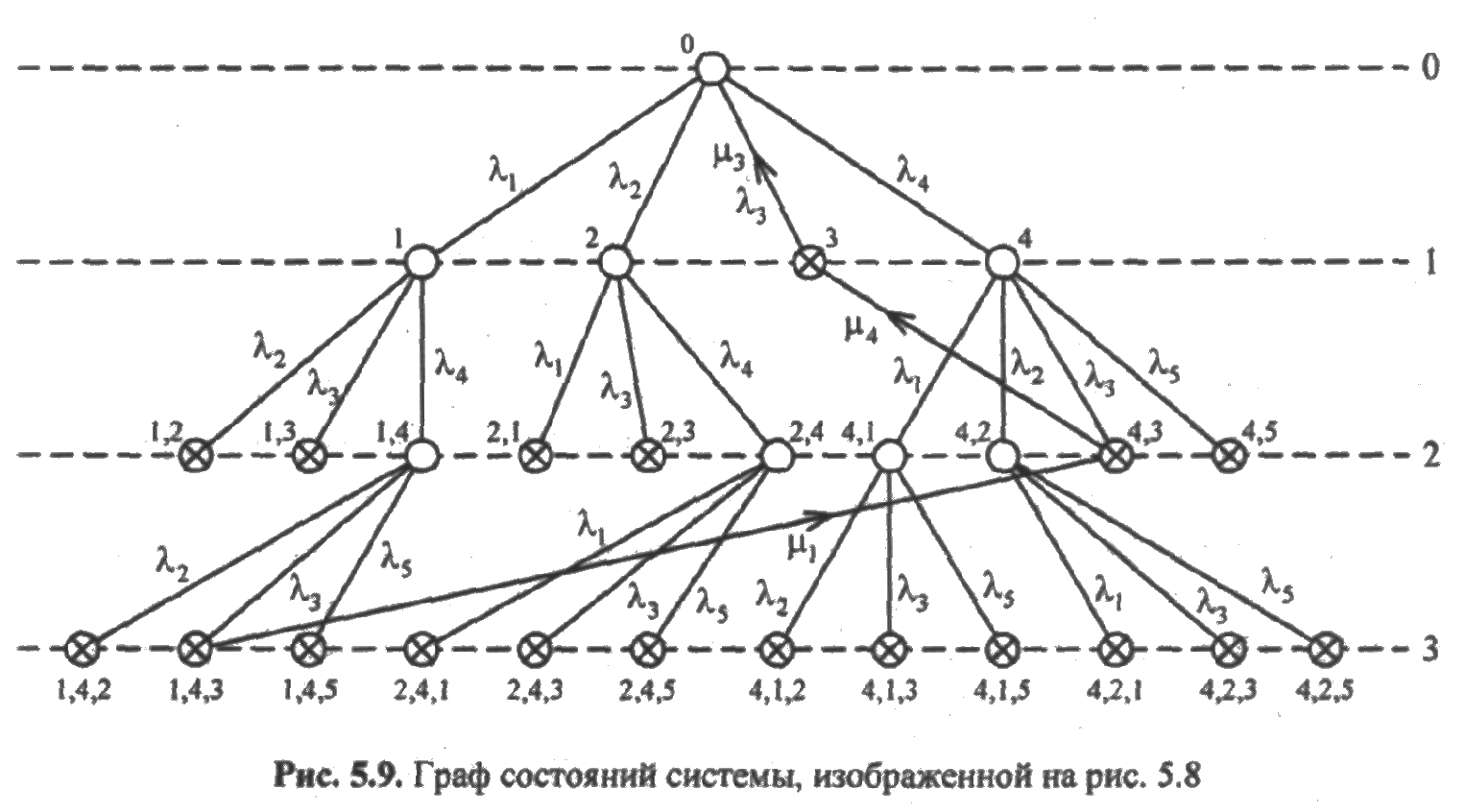
Решение. Греф состояний системы приведен на рис. 5.9.

Граф имеет четыре уровня. В исходном нулевом состоянии система исправна и ни один из ее элементов не отказал. Все состояния последнего третьего уровня соответствуют отказовым состояниям системы. При простейшем потоке отказов, удовлетворяющем условиям ординарности, система может перейти из начального нулевого состояния в состояния, когда отказал один любой ее элемент. Эти состояния отмечены на линии уровня 1 цифрами 1, 2, 3, 4 в соответствии с отказавшими элементами структурной схемы. На линии первого уровня отсутствует узел с номером 5. Это объясняется тем, что пятый элемент находится в ненагруженном резерве и по условию задачи отказать до замещения основного четвертого элемента не может. Из структурной схемы видно, что отказ элемента 3 приводит к отказу всей системы. Поэтому узел 3 первого уровня помечен крестом и из этого узла отсутствуют переходы в узлы второго уровня. Отказ одного из элементов 1, 2, 4 не ведет к отказу системы, поэтому из узлов 1, 2, 4 первого уровня имеются переходы в узлы второго уровня.

Из состояния (1) первого уровня возможны переходы в состояния, когда вслед за отказом элемента 1 отказывает либо элемент 2, либо элемент 3, либо элемент 4. Эти состояния на линии второго уровня отмечены соответственно (1,2), (1,3), (1,4). Так как отказ элементов 1,2 или 1,3 ведет к отказу системы, то состояния (1,2) и (1,3) отмечены крестами и из этих состояний отсутствуют переходы в состояния уровня 3. При отказе элементов 1 и 4 отказ системы не наступает, поэтому из состояния (1,4) возможны переходы в состояния третьего уровня. Вслед за отказами элементов 1 и 4 могут отказать элементы либо 2, либо 3, либо 5. Соответствующие состояния расположены на линии уровня 3 и обозначены (1,4,2), (1,4,3), (1,4,5). Так как отказ элементов 1,4, 2 или 1,4,3, или 1,4,5 ведет к отказу системы, то все узлы отмечены крестами Остальная часть графа строится аналогично.

Для окончательного построения графа необходимо на графе состояний с λ -переходами изобразить ветви переходов из узлов нижних уровней в узлы верхних уровней. Эти переходы возникают из-за восстановления отказавших элементов. Узлы, соединенные между собой ветвями μ -переходов, легко определить, если известен приоритет в обслуживании отказавших элементов.

Пусть, например, система попала в состояние, отмеченное на линии уровня графа состояний как (1,4,3). И пусть установлен прямой приоритет в обслуживании отказавших элементов (обслуживание элементов осуществляется порядке их отказов). Тогда первым будет восстановлен элемент 1 и система интенсивностью μ ₁ перейдет в состояние (4,3) второго уровня. Состояние (4,3) является отказовым, поэтому, пока ремонтируется элемент 4, новых отказов не возникает. После ремонта элемента 4 система перейдет с интенсивностью μ₄ в состояние (3) первого уровня, затем с интенсивностью μ ₃ в нулевое состояние. Указанные переходы показаны на рис. 5.9.

Пусть теперь отказавшие элементы обслуживаются с обратным приоритетом, т. е. восстановление элементов осуществляется в порядке, обратном очередности поступления их в ремонт. Тогда из состояния (1,4,3) возможен переход с интенсивностью λ ₃ в состояние (1,4), потом с интенсивностью λ ₄ — в состояние (1) и затем с интенсивностью λ₁, — в нулевое состояние.

Описание функционирования системы с помощью графов позволяет сформировать ряд важных общих свойств графов состояний.

1. Граф состояний полностью описывает функционирование восстанавливаемой системы, как системы массового обслуживания. Вид графа зависит от структурной схемы системы, надежности и ремонтопригодности элементов, а также от дисциплины обслуживания. На основании этого свойства можно утверждать, что все количественные характеристики надежности восстанавливаемой системы могут быть определены непосредственно из графа состояний системы.

2. Число узлов графа может быть больше или меньше возможного числа состояний восстанавливаемой системы. Это объясняется тем, что граф описывает поведение системы совместно с функционированием обслуживающего органа, т. е. он описывает функционирование системы массового обслуживания.

3. Граф, не содержащий поглощающих состояний, описывает поведение восстанавливаемой системы при неограниченном ремонте, т. е. описывает поведение системы, функционирующей бесконечно долго.

4. Функционирование восстанавливаемой системы с одним ремонтным органом и обратным приоритетом в обслуживании отказавших элементов описывается графом типа дерева.

Date: 2015-07-17; view: 1444; Нарушение авторских прав