Сущность логико-вероятностных методов

Любой метод анализа надежности требует описания условий работоспособности системы. Такие условия могут быть сформулированы на основании:

- структурной схемы функционирования системы (схемы расчета надежности);

- словесного описания функционирования системы;

- граф-схемы;

- функции алгебры логики.

Логико-вероятностный метод анализа надежности позволяет формализовать определение и смысл благоприятных гипотез. Сущность этого метода состоит в следующем.

· Состояние каждого элемента кодируется нулем и единицей:

В функциях алгебры логики состояния элементов представляются в следующем виде:

• х _i — исправное состояние элемента, соответствующее коду 1;

• — отказовое состояние элемента, соответствующее коду 0.

- Записывается с помощью функций алгебры логики условие работоспособности системы через работоспособность (состояние) ее элементов. Полученная функция работоспособности системы является двоичной функцией двоичных, аргументов.

- Полученная ФАЛ преобразуется таким образом, чтобы в ней содержались члены, соответствующие благоприятным гипотезам исправной работы системы.

- В ФАЛ вместо двоичных переменных х_i и подставляются вероятности соответственно безотказной работы р_i и вероятности отказа q_i. Знаки конъюнкции и дизъюнкции заменяются алгебраическими умножением и сложением.

Полученное выражение и есть вероятность безотказной работы системы P_c(t).

Рассмотрим логико-вероятностный метод на примерах.

ПРИМЕР 5.10. Структурная схема системы представляет собой основное (последовательное) соединение элементов (рис. 5.14).

На структурной схеме х_i, i = 1, 2,..., п — состояние i -го элемента системы, кодируемое 0, если элемент находится в отказовом состоянии, и 1, если он исправный. В данном случае система исправна, если исправны все ее элементы. Тогда ФАЛ является конъюнкцией логических переменных, т.е. у=x₁,x₂,…..,х_п, представляющей собой совершенную дизъюнктивно нормальную форму системы.

Подставляя вместо логических переменных вероятности исправных состояний элементов и, заменяя конъюнкцию на алгебраическое умножение, получим:

ПРИМЕР 5.11. Структурная схема системы представляет собой дублированную систему с неравнонадежными, постоянно включенными подсистемами (рис. 5.15).

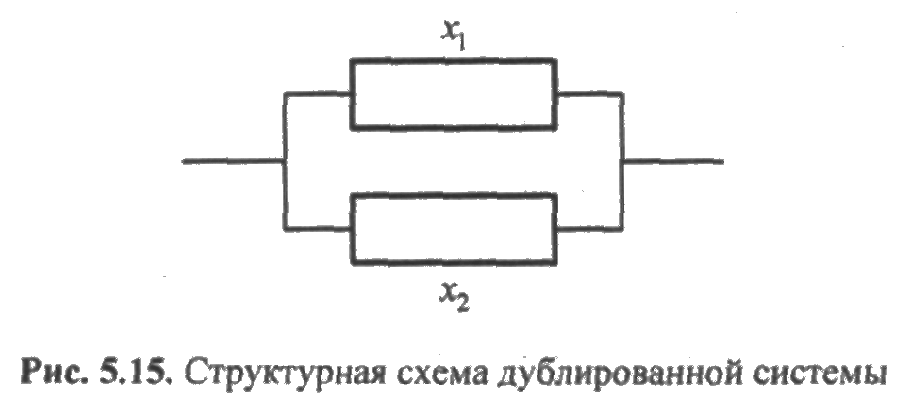
На рис. 5.15 х₁ и х₂ — состояния элементов системы. Составим таблицу истинности двух двоичных переменных (табл. 5.2).

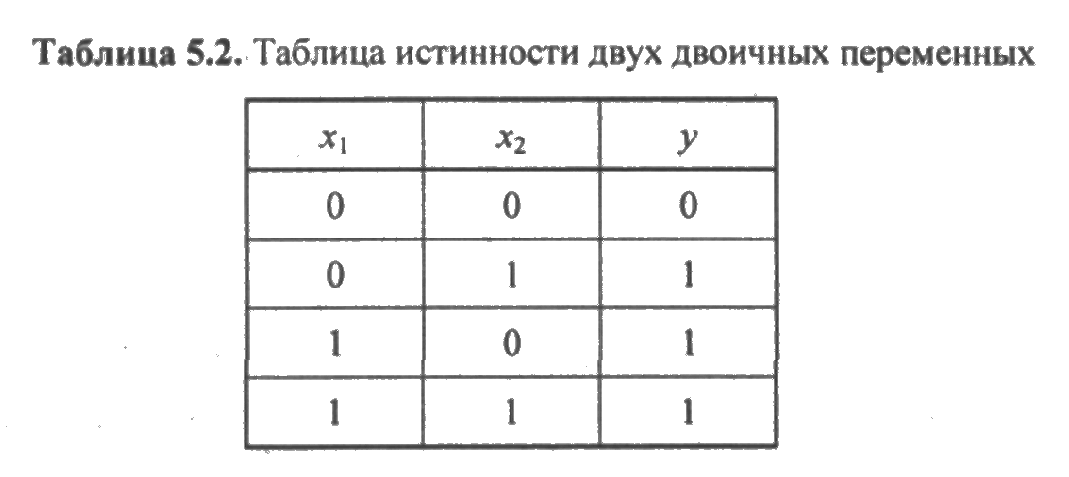
В таблице 0 — отказовое состояние элемента, 1 — исправное состояние элемента. В данном случае система исправна, если исправны оба элемента (1,1) или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы описывается следующей функцией алгебры логики:

Этафункция является совершенной дизъюнктивной нормальной формой. Заменяя операции дизъюнкции и конъюнкции на алгебраические операции умножения и сложения, а логические переменные — на соответствующие вероятности состояния элементов, получим вероятность безотказной работы системы:

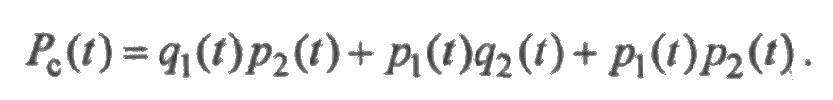
ПРИМЕР 5.12. Структурная схема системы имеет вид, показанный на рис. 5.16.

Составим таблицу истинности (табл. 53).

В данном примере система исправна, если исправны все ее элементы или исправным является элемент x_i и один из элементов дублированной пары (х₂, х₃). На основании таблицы истинности СДНФ будет иметь вид:

Подставляя вместо двоичных переменных соответствующие вероятности, а вместо конъюнкций и дизъюнкций — алгебраические умножение и сложение, получим вероятность безотказной работы системы:

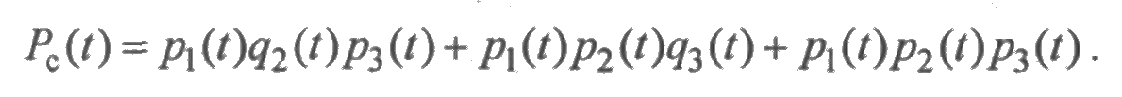
Функцию алгебры логики можно представить в минимальной форме, если воспользоваться следующими преобразованиями:

Операции поглощения и склеивания в алгебре не применимы. В связи с этим нельзя полученную ФАЛ минимизировать, а затем вместо логических переменных подставлять значения вероятностей. Вероятности состояний элементов следует подставлять в СДНФ, а упрощать по правилам алгебры.

Недостатком описанного метода является необходимость составления таблицы истинности, что требует перебора всех работоспособных состояний системы.

5.3.2. Метод кратчайших путей и минимальных сечений

Этот метод был рассмотрен ранее в разд. 5.2.3. Изложим его с позиции алгебры логики.

Функцию работоспособности можно описать с помощью кратчайших путей пешного функционирования системы и минимальных сечений ее отказа.

Кратчайшим путем называется минимальная конъюнкция работоспособных:стояний элементов, образующих работоспособную систему.

Минимальным сечением называется минимальная конъюнкция неработоспособных состояний элементов, образующих неработоспособное состояние системы.

ПРИМЕР 5.13. Необходимо образовать функцию работоспособности системы структурная схема которой приведена на рис. 5.17, используя метод кратчайших путей и минимальных сечений.

Решение. В данном случае кратчайшими путями, образующими работоспособную систему, будут: х₁х₂, х₃х₄,, х₁х₅х₄, х₃х₅х₂. Тогда функция работоспособности запишется в виде следующей функции алгебры логики:

В соответствии с этой ФАЛ структурная схема системы рис. 5.17 может быть представлена структурной схемой рис. 5.18.

Минимальными сечениями, образующими неработоспособную систему, будут: х₁х₃, х₂х₄,, х₁х₅х₄, х₃х₅х₂. Тогда функция неработоспособности запишется в виде следующей функции алгебры логики:

В соответствии с этой ФАЛ структурная схема системы будет представлена в виде, показанном на рис. 5.19.

Следует иметь в виду, что структурные схемы рис. 5.18 и рис. 5.19 не являются схемами расчета надежности, а выражения для ФАЛ работоспособного и неработоспособного состояний не являются выражениями для определения вероятности безотказной работы и вероятности отказа:

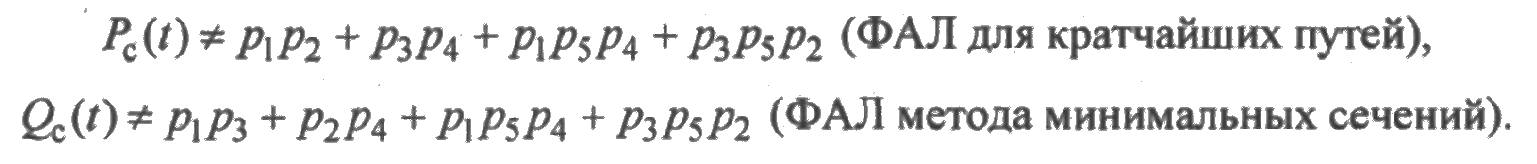
Основные достоинства ФАЛ в том, что они позволяют получить формально, не составляя таблицы истинности, СДНФ и СКНФ (совершенная конъюнктивная нормальная форма), которые дают возможность получить вероятность безотказной работы (вероятность отказа) системы путем подстановки в ФАЛ вместо логических переменных соответствующих значений вероятностей безотказной работы, заменив операции конъюнкции и дизъюнкции на алгебраические операции умножения и сложения.

Для получения СДНФ необходимо каждый дизъюнктивный член ФАЛ умножить на , где х_i — недостающий аргумент, и раскрыть скобки. Ответом будет СДНФ. Рассмотрим этот способ на примере.

ПРИМЕР 5.14. Необходимо определить вероятность безотказной работы системы, структурная схема которой приведена на рис. 5.17. Вероятности безотказной работы элементов равны р₁, р₂, р₃, р₄, р₅.

Решение. Воспользуемся методом кратчайших путей. Функция алгебры логики, полученная методом кратчайших путей, имеет вид:

Получим СДНФ системы. Для этого умножим дизъюнктивные члены на недостающие :

Раскрывая скобки и выполняя преобразования по правилам алгебры логики, получим СДНФ:

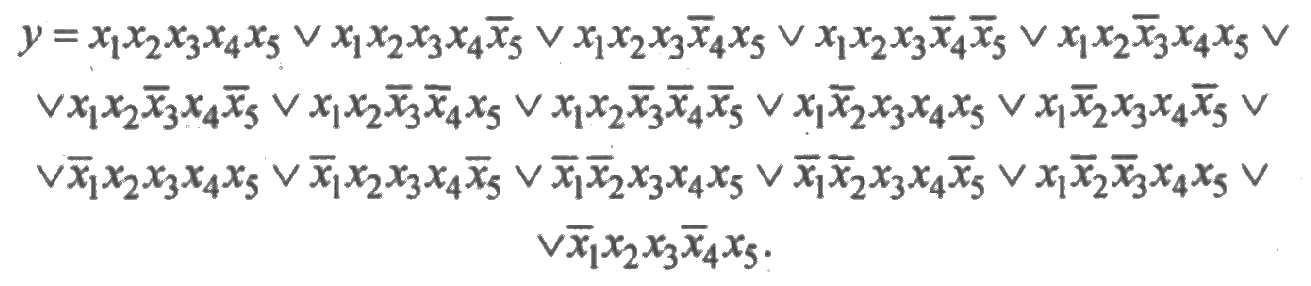
Подставляя в СДНФ вместо х₁, х₂, х₃, х₄, х₅ вероятности безотказной работы р₁, р₂, р₃, р₄, р₅ и используя соотношения q_i = 1– р_i, получим следующее выражение для вероятности безотказной работы системы.

Из приведенного примера видно, что метод кратчайших путей освободил нас от определения благоприятных гипотез. Тот же результат можно получить, если воспользоваться методом минимальных сечений.

5.3.3. Алгоритм разрезания

Алгоритм разрезания позволяет получить ФАЛ, подставляя в которую вместо логических переменных вероятности безотказной работы (вероятности отказа) элементов можно найти вероятность безотказной работы системы. Получения для этой цели СДНФ не требуется.

Алгоритм разрезания основан на следующей теореме алгебры логики: функция алгебры логики у(х_ь х₂,...,х_п) может быть представлена в следующей форме:

Покажем применимость этой теоремы на трех примерах:

Применяя второй распределительный закон алгебры логики, получим:

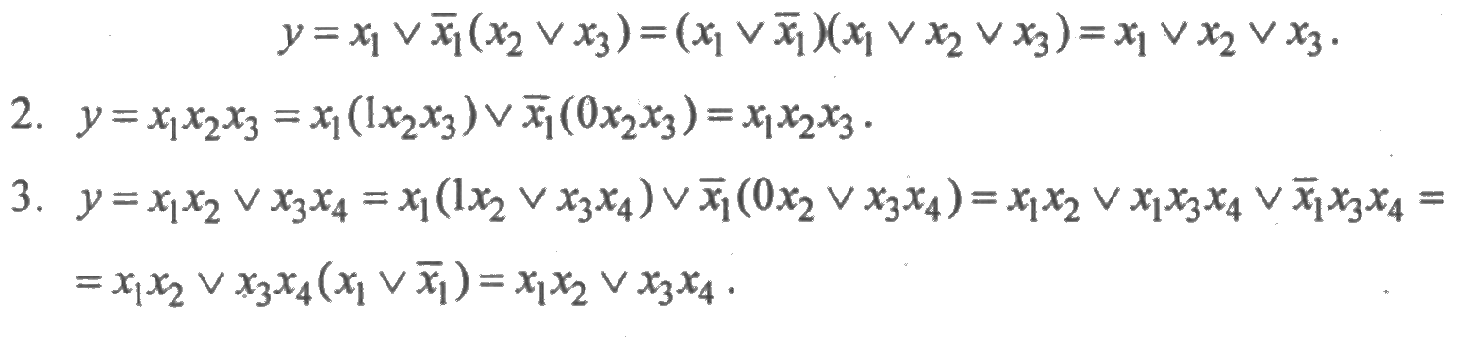
ПРИМЕР 5.15. Определить вероятность безотказной работы системы, струк­турная схема которой представлена на рис. 5.16, воспользовавшись алгоритмом разрезания.

Решение. Используя метод кратчайших путей, получим следующую ФАЛ:

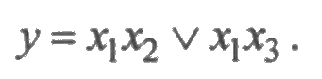
Применим алгоритм разрезания:

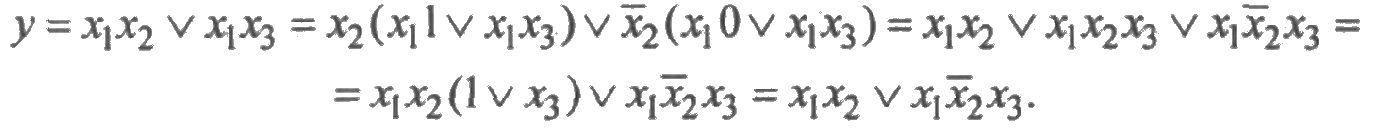
Подставляя теперь вместо логических переменных вероятности и заменяя операции конъюнкции и дизъюнкции на алгебраические умножение и сложение, получим:

ПРИМЕР 5.16. Определить вероятность безотказной работы системы, структурная схема которой приведена на рис. 5.17. Воспользоваться алгоритмом разрезания.

Решение. Функция алгебры логики, полученная методом минимальных сечений, имеет вид:

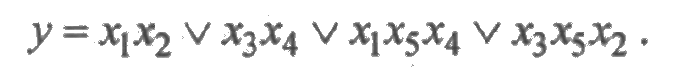
Реализуем алгоритм разрезаний относительно х ₅:

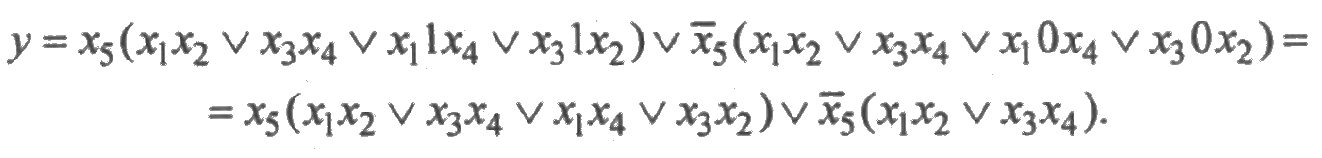
Упростим полученное выражение, пользуясь правилами алгебры логики. Вы-ражение в первых скобках упростим, используя правило выноса за скобки:

Тогда ФАЛ будет иметь вид:

Этому выражению соответствует структурная схема рис. 5.20.

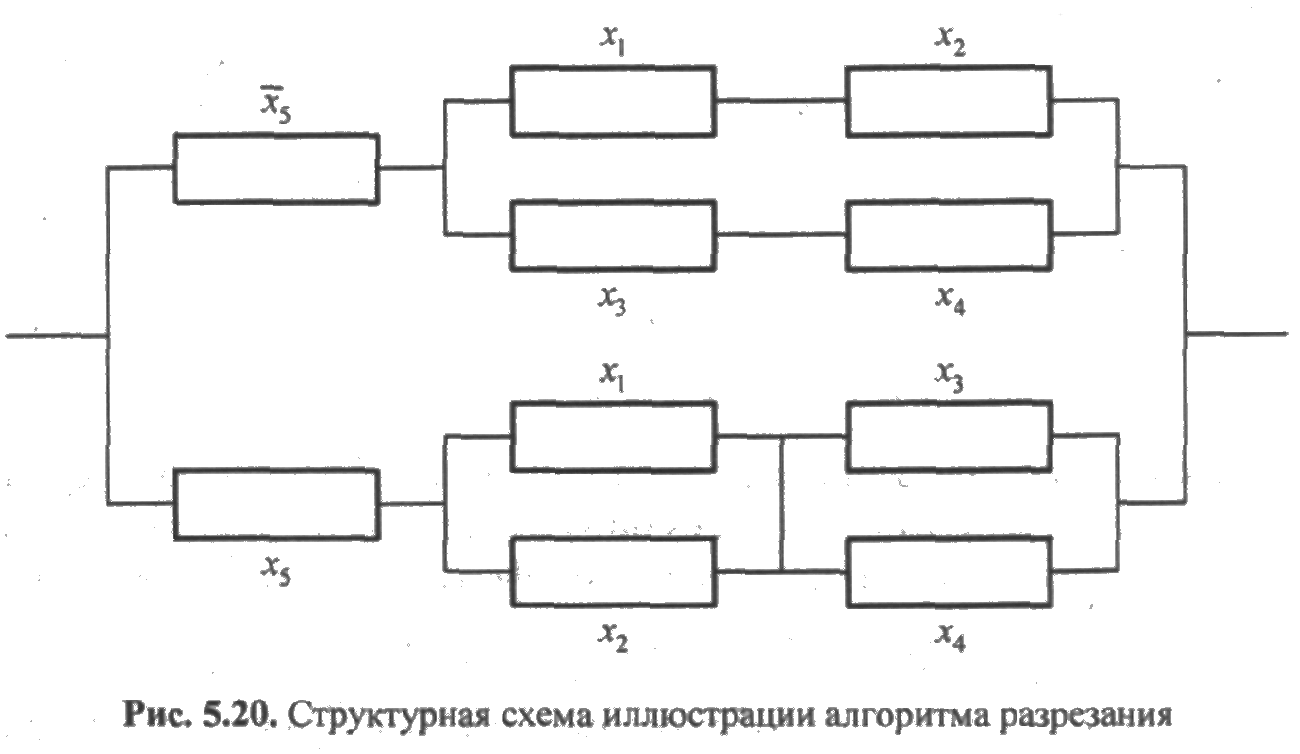
Полученная схема является также схемой расчета надежности, если логические переменные заменить вероятностями безотказной работы р₁, р₂, р₃, р₄, р₅, а переменную — вероятностью отказа q₅. Из рис. 5.20 видно, что структурная схема системы сведена к последовательно-параллельной схеме. Вероятность безотказной работы вычисляется по следующей формуле:

Формула в объяснении не нуждается, она записана непосредственно по структурной схеме.

5.3.4. Алгоритм ортогонализации

Алгоритм ортогонализации, как и алгоритм разрезания, позволяет формальными процедурами образовать функцию алгебры логики, подставляя в которую вместо логических переменных вероятности, а вместо дизъюнкций и конъюнкции — алгебраические сложение и умножение, получить вероятность безотказной работы системы. Алгоритм основан на преобразовании функций алгебры логики в ортогональную дизъюнктивную нормальную форму (ОДНФ), которая существенно короче СДНФ. Прежде чем излагать методику, сформулируем ряд определений и приведем примеры.

Две конъюнкции называются ортогональными, если их произведение тождественно ноль. Дизъюнктивная нормальная форма называется ортогональной, если все ее члены попарно ортогональны. СДНФ является ортогональной, но самой длинной из всех ортогональных функций.

Ортогональную ДНФ можно получить с помощью следующих формул:

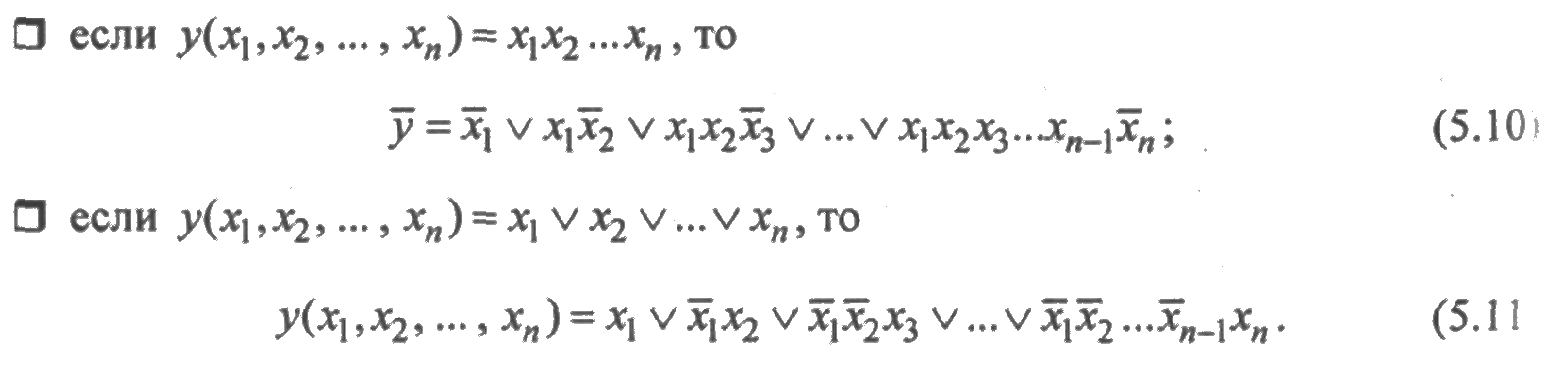
Эти формулы легко доказать, если воспользоваться вторым распределительным законом алгебры логики и теоремой де-Моргана. Алгоритмом получение ортогональной дизъюнктивной нормальной формы является следующая процедура преобразования функции у(х₁,х₂,..., х_п) в ОДНФ:

- функция у(х₁,х₂,..., х_п) преобразуется в ДНФ с помощью метода кратчайших путей или минимальных сечений;

- находится ортогональная дизъюнктивно-нормальная форма с помощью формул (5.10) и (5.11);

- минимизируется функция путем приравнивания к нулю ортогональных членов ОДНФ;

- логические переменные заменяются вероятностями безотказной работы (вероятностями отказов) элементов системы;

- окончательное решение получается после упрощения выражения, полученного на предыдущем шаге.

Рассмотрим методику на примере.

ПРИМЕР 5.17. Определить вероятность безотказной работы системы, струк­турная схема которой приведена на рис. 5.17. Применить метод ортогонализации.

Решение. В данном случае функционирование системы описывается следующей функцией алгебры логики (метод минимальных сечений):

Обозначим К₁ = х₁х₂, К₂ = х₃х₄, К₃ = х₁х₅х₄, К₄ = х₃х₅х₂. Тогда ОДНФ запишется в следующем виде:

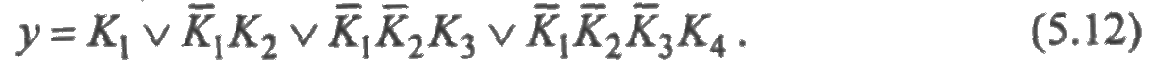
Значения , i = 1,2,3, на основании формулы (5.10) будут иметь вид:

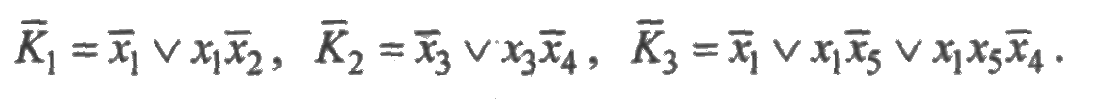
Тогда

Подставляя эти выражения в (5.12), получим:

Заменяя в этом выражении логические переменные соответствующими вероятностями и выполняя алгебраические операции сложения и умножения, по­лучим вероятность безотказной работы системы:

Ответ совпадает с полученным в примере 5.14.

Из примера видно, что алгоритм ортогонализации более производительный, чем способы, рассмотренные ранее. Более подробно логико-вероятностные методы анализа надежности изложены в [72,99]. Логико-вероятностный метод, как и любой другой, имеет свои достоинства и недостатки. О его достоинствах было сказано ранее. Укажем его недостатки.

Исходными данными в логико-вероятностном методе являются вероятности безотказной работы элементов структурной схемы системы. Однако во мно­гих случаях эти данные не могут быть получены. И не потому, что надежность элементов неизвестна, а потому, что время функционирования элемента является случайной величиной. Это имеет место в случае резервирования замещением, наличия последействия отказов, неодновременноcти работы элементов, наличия восстановления с различной дисциплиной обслуживания и во многих других случаях.

Приведем примеры, иллюстрирующие эти недостатки. Структурная схема системы имеет вид, показанный на рис. 5.21, где приняты следующие обозначения: x_i — логические переменные, имеющие значения 0 и 1, соответствующие отказу и исправной работе элемента, x_i = 1, 2, 3.

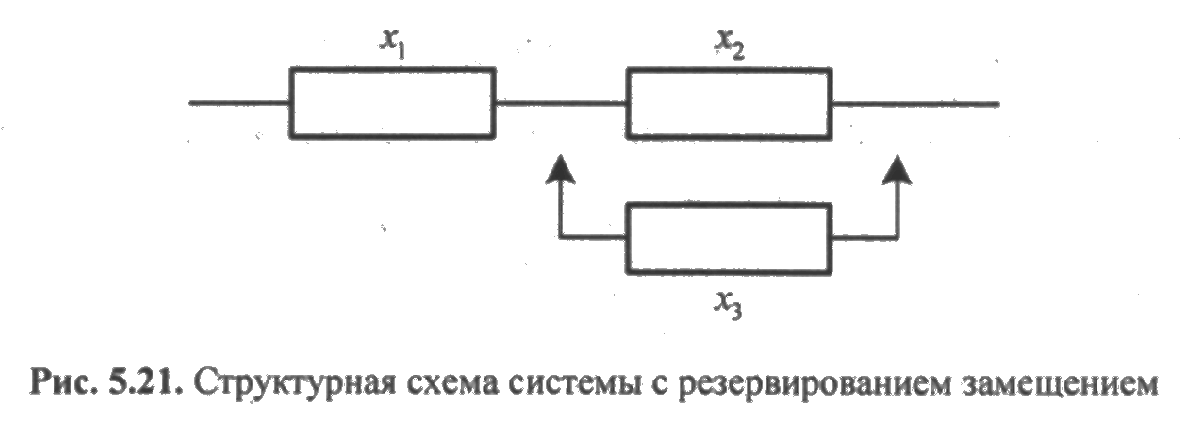
В данном случае логическая переменная дс₃ является 0 до момента времени τ отказа основного элемента и 1 в течение времени (t-τ), где t — врем, в течение которого определяется вероятность безотказной работы системы. Время τ является величиной случайной, поэтому значение р(τ) неизвестно. В данном случае составить ФАЛ и тем более СДНФ невозможно. Ни один израссмотренных нами логико-вероятностных методов не позволяет найти вероятность безотказной работы системы.

Вот еще один типичный пример. Энергетическая система состоит из регулятора напряжения R _н и двух параллельно работающих генераторов Г₁ и Г₂. Структурная схема системы показана на рис. 5.22.

При отказе одного из генераторов оставшийся исправным работает один общую нагрузку. Его интенсивность отказов увеличивается. Если до момента τ отказа одного из генераторов интенсивность его отказа была равна λ, то после отказа λ₁ > λ₂. Так как время τ является величиной случайной, то Р(τ) неизвестно. Здесь, как и в случае резервирования замещением, логико-вероятностные методы бессильны. Таким образом, указанные недостатки логико-вероятностных методов снижают их практическое применение при расчете надежности сложных систем.

5.4. Топологические методы анализа надежности

Топологическими будем называть методы, которые позволяют определить показатели надежности либо по графу состояний, либо по структурной схеме системы, не составляя и не решая уравнений. Топологическим методам посвящен ряд работ [84,147], в которых описаны различные способы их практической реализации. В настоящем разделе излагаются методы, позволяющие определить показатели надежности по графу состояний.

Топологические методы дают возможность вычислять следующие показатели надежности:

- Р(t) — вероятность безотказной работы в течение, времени t;

- T₁, — среднее время безотказной работы;

- К_г(t) — функцию готовности (вероятность того, что система исправна в любой произвольный момент времени t);

- К_г = — коэффициент готовности;

T — наработку на отказ восстанавливаемой системы.

Топологические методы имеют следующие особенности:

- простота вычислительных алгоритмов;

- высокая наглядность процедур определения количественных характери­стик надежности;

- возможность приближенных оценок;

- отсутствие ограничений на вид структурной схемы (системы, восстанавливаемые и невосстанавливаемые, нерезервированные и резервированные с любым видом резервирования и любой кратностью).

В настоящей главе будут рассматриваться ограничения топологических методов:

- интенсивности отказов и восстановления элементов сложной системы являются величинами постоянным»;

- временные показатели надежности, такие как вероятность безотказной работы и функция готовности, определяются в преобразованиях Лапласа;

- трудности, в ряде случаев непреодолимые, при анализе надежности сложных систем, описываемых многосвязным графом состояний.

Идея топологических методов состоит в следующем.

Граф состояний является одним из способов описания функционирования системы. Он определяет вид дифференциальных уравнений и их количество. Интенсивности переходов, характеризующие надежность элементов и их восстанавливаемость, определяют коэффициенты дифференциальных уравнений. Начальные условия выбираются кодированием узлов графа.

В графе состояний содержится вся информация о надежности системы. А это является основанием считать, что показатели надежности могут быть вычислены непосредственно по графу состояний.

5.4.1. Определение вероятностей состояний системы

Вероятность застать восстанавливаемую систему в состоянии i в фиксированный момент времени t в преобразовании Лапласа может быть записана в следующем виде:

где Δ(s) — главный определитель системы дифференциальных уравнений, записанной в преобразованиях Лапласа; Δ_i(s) — частный определитель системы.

Из выражения (5.13) видно, что P_i(s) будет определена, если из графа состояний будут найдены степени тип полиномов числителя и знаменателя, а также коэффициенты B_ij (j = 0,1,2,..., m) и А_i (i = 0,1, 2,..., n -1).

Первоначально рассмотрим методику определения P_i(s) графа состояний только таких систем, в графе состояний которых отсутствуют переходы через состояния. К ним относятся все неизбыточные системы, резервированные системы при общем резервировании с целой и дробной кратностью, резервированные системы любой структуры с обслуживанием отказавших устройств в последовательности, обратной их поступлению в ремонт. К указанному классу систем относятся также некоторые резервированные системы с равнонадежными устройствами при различной дисциплине их обслуживания.

Функционирование системы описывается дифференциальными уравнениями, число которых равно числу узлов графа. Это значит, что главный определитель системы Δ(s) в общем случае будет полиномом n-й степени, где n — число узлов графа состоянии. Легко показать, что полином знаменателя не содержит свободного члена. Действительно, т.к. то знаменатель функции Pi(s) должен содержать s в качестве сомножителя, в противном случае финальная вероятность Pi(∞) будет равна нулю. Исклю­чением являются случаи, когда число ремонтов ограничено.

Степень полинома числителя Δ_i находится из выражения:

m_i = n - 1 – l_i,

Где n — число узлов графа состояний; li — число переходов из начального состояния системы, определенного начальными условиями ее функционирования, в состояние i по кратчайшему пути.

Если начальным состоянием системы является состояние, когда все устройства исправны, то l_i — номер уровня состояния i, т.е. l_i равно минимальному числу отказавших устройств системы в состоянии i. Таким образом, степень полинома числителя вероятности Р_i(s) пребывания системы в i -м состоянии зависит от номера состояния i и от начальных условий. Так как число переходов l_i может быть 0,1,2,..., n -1, то степень полинома Δ_i(s) на основании (5.14) также может принимать значения m_i = 0,1,2,..., n -1.

Date: 2015-07-17; view: 2270; Нарушение авторских прав