Математические модели функционирования

ТЕХНИЧЕСКИХ ЭЛЕМЕНТОВ И СИСТЕМ В СМЫСЛЕ ИХ НАДЕЖНОСТИ

Расчет надежности сложных технических систем часто базируется на предположении о том, что время безотказной работы и время восстановления элементов имеют экспоненциальные распределения вероятностей. Как было показано в гл. 3, это допущение приводит к существенным ошибкам при вычислении показателей надежности. Более реальным является анализ надежности технических систем, если снять ограничения об экспоненциальности распределений времени до отказа, восстановления и.случайных параметров, сопутствующих функционированию системы. К таким параметрам относятся: время между очередными сеансами контроля и время его проведения, момент подключения в работу резервных элементов, время между очередными профилактиками и время их проведения и т. п.

4.1. Общая модель надежности технического элемента

Напомним, что под элементом в теории надежности понимается любой технический объект, имеющий показатель надежности, самостоятельно учитываемый при расчетах.

Элемент с восстановлением имеет два возможных состояния:

□ (0) — элемент работает;

□ (1) — элемент восстанавливается.

Пусть Y₀(s,t) — вероятность того, что на интервале [ t, t+s ] элемент находится в исправном состоянии, а Y₁(τ,t) — вероятность того, что на интервале [ t, t+τ ] элемент восстанавливается. Продифференцируем эти функции:

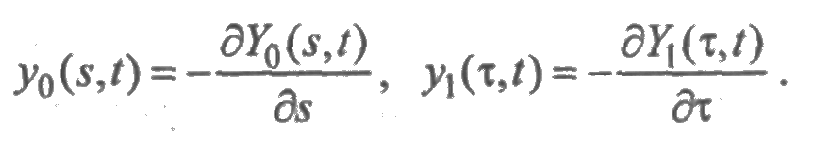
Функция y ₀ (s,t) представляет собой плотность распределения вероятностей исправной работы элемента на интервале [ t, t+s ], а функция y ₁ (τ,t) — плотность распределения вероятностей времени восстановления элемента на интервале [ t, t+τ ].

Предположим, что в начальный момент времени t =0 элемент находится в исправном состоянии, тогда

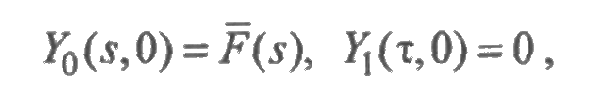
и потому

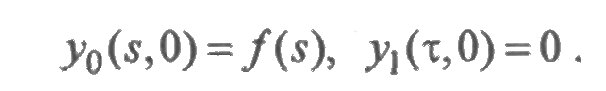
Момент перехода из состояния восстановления в состояние исправной работы показан на рис. 4.1.

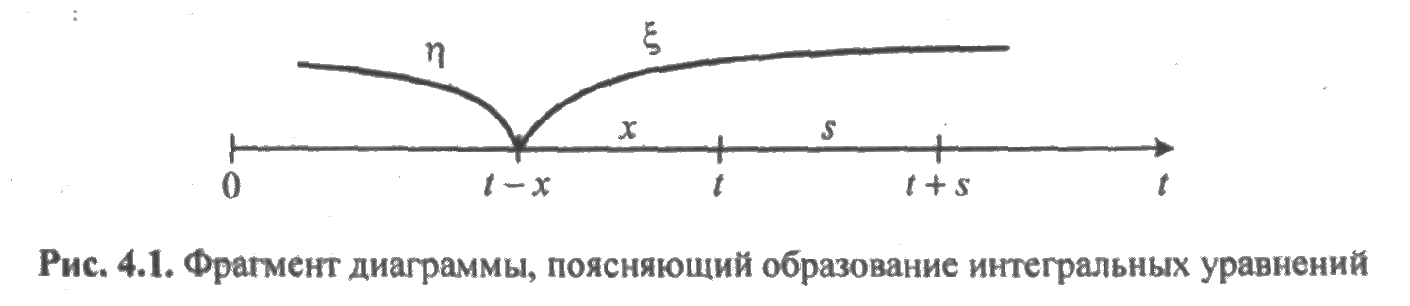
На рис. 4.1 приняты следующие обозначения:

ξ— случайное время исправной работы элемента;

η — случайное время восстановления элемента;

t — момент времени, при котором элемент исправен;

х — произвольный момент времени, взятый на промежутке от 0 до t;

t - х — момент окончания восстановления отказавшего элемента;

s — время, в течение которого элемент исправен.

Вероятность того, что элемент исправно работал в течение времени х + s при условии, что в момент времени t-х произошло его восстановление, равна y₁(0,t-x)f(x+s).

Так как x — любой момент времени из интервала [0; t ], то в результате интегрирования этой функции от 0 до t получим уравнение

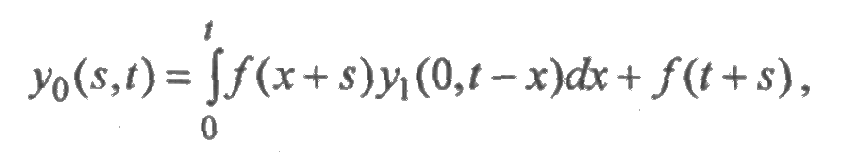
в котором слагаемое f(t+s) обусловлено началом процесса функционирования и означает, что при отсутствии отказа до момента t элемент работает безотказно в течение времени (t+s). Аналогичное уравнение имеет место и для второй функции y ₁(τ ,t), но уже без свободного члена.

Это позволяет записать следующую систему интегральных уравнений относительно функций y₀ и y ₁:

Система уравнений (4.1) связывает между собой две функции, содержащие предысторию процесса функционирования элемента. Это обусловлено наличием в аргументах функций y ₀(s ,t) и y ₁(τ ,t) дополнительных переменных s и τ, которые соответствуют остаточному времени работы и восстановления элемента.

Если остаточное время работы и восстановления равно нулю, то функции ω(t) = y ₀(0 ,t) и ω_B(t) = y ₁(0 ,t) являются параметрами потока отказов и восстановления соответственно. Обозначая φ_s(t) = φ(t+s), получим:

Последние формулы дают возможность выразить вероятности Y₀ при малых s и Y₁ при малых τ через важнейшие характеристики элемента: функции готовности и простоя и параметры потока отказов и восстановлений. Выражения имеют вид:

Тогда

Полагая в (4.2) s =0 и τ=0, получим

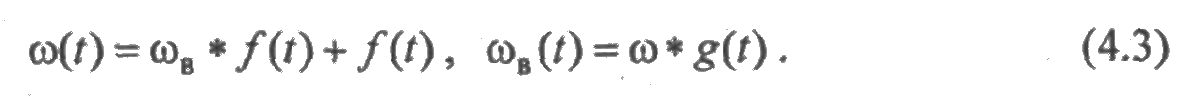
Отсюда следует, что

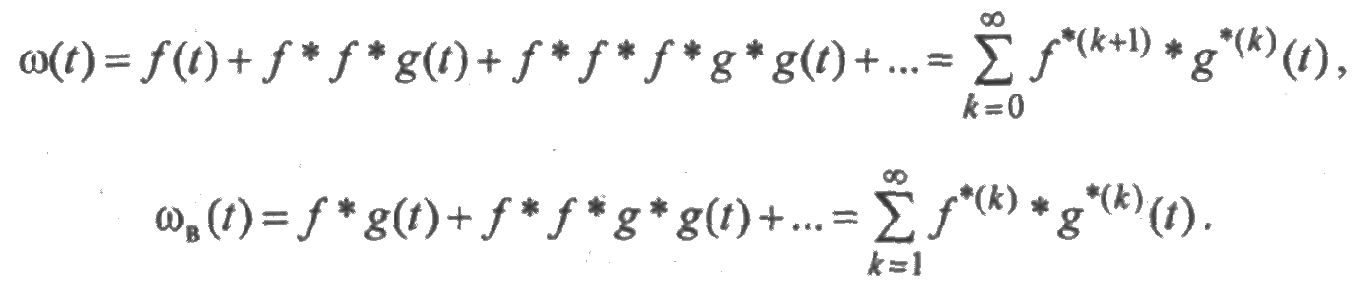
Вероятности р₀(t) и р₁(t) пребывания элемента в исправном и отказовом состояниях, очевидно, совпадают соответственно с функциями готовности и простоя. Нетрудно показать, что эти вероятности удовлетворяют уравнениям, аналогичным уравнениям Эрланга

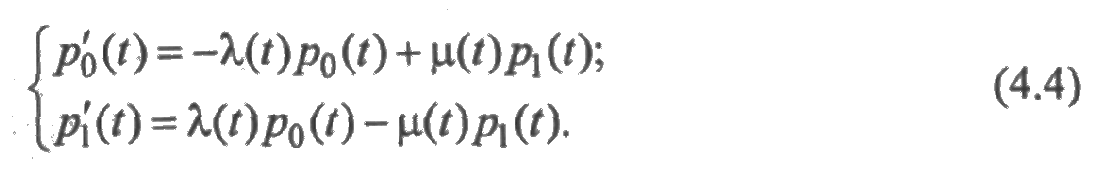
Здесь λ(t) и μ(t) — интенсивности потоков отказов и восстановлений, определенные в разд. 2.6. Отсюда следует, что работу элемента можно описать простейшим графом состояний (рис. 4.2), в ветвях которого находятся функции λ(t) и μ(t). Этому графу соответствует система обыкновенных дифференциальных уравнений (4.4).

Согласно принятому ранее допущению вероятности р₀(t) и р₁(t) удовлетворяют начальным условиям: р₀(0)=1 и р₁(0)=0, означающим, что в момент времени t = 0 элемент исправен.

Следует иметь в виду, что решить систему уравнений (4.1) проще, чем вначале определять интенсивности λ(t) и μ(t), а затем решать систему дифференциальных уравнений (4.4). Наоборот, указанные интенсивности могут быть определены в результате решения системы (4.1).

Аналогичные рассуждения позволяют записать для оценки надежности математическую модель функционирования любой сложной системы. В следующем разделе мы получим такую модель в достаточно общей ситуации, однако для ее составления применим несколько иной способ.

ПРИМЕР 4.1. Предположим, что время безотказной работы и время восстановления элемента имеют экспоненциальные распределения с параметрами λ(t) и μ(t) соответственно. Требуется получить выражения для параметров потоков отказов и восстановлений, среднего суммарного числа отказов и восстановлений в течение времени [0; t ], функций готовности и простоя, средней суммарной наработки и суммарного времени восстановления элемента в течение времени [0; t ].

Решение. Из соотношений (4.3) на основании разд. 2.5 параметры потоков отказов и восстановлений в преобразовании Лапласа имеют вид:

отсюда

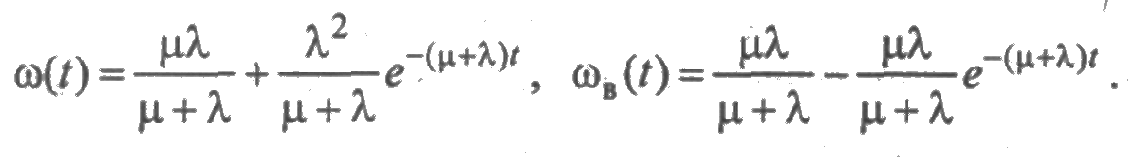
На основе формул ~разд. 2.6 определим среднее суммарное число отказов и среднее суммарное число восстановлений в течение времени [0; t ]:

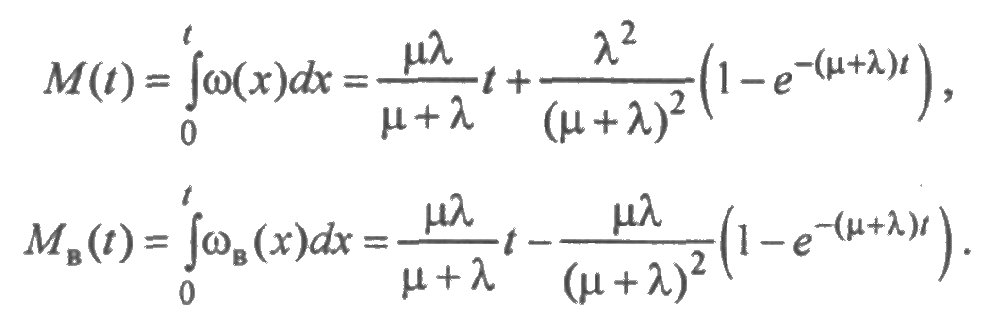
Из соотношений (2.32) и (4.3) функции готовности и простоя в преобразовании Лапласа имеют вид:

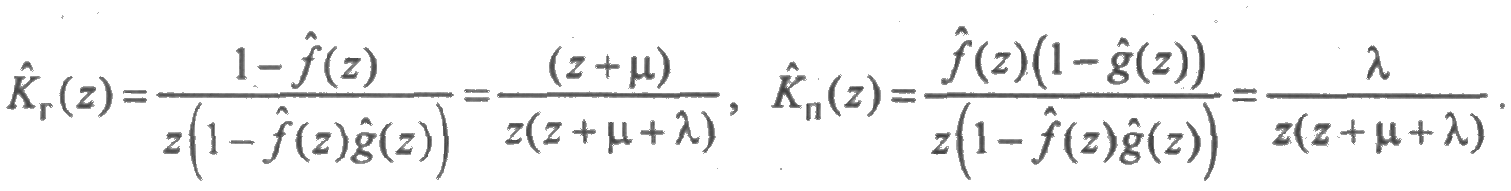
Отсюда

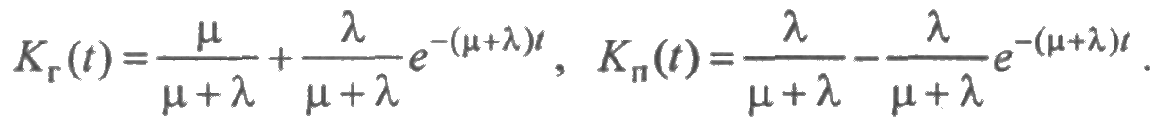
На основе формул разд. 2.6 определим среднее суммарное время безотказной работы и среднее суммарное время восстановления в течение времени [0; t ]:

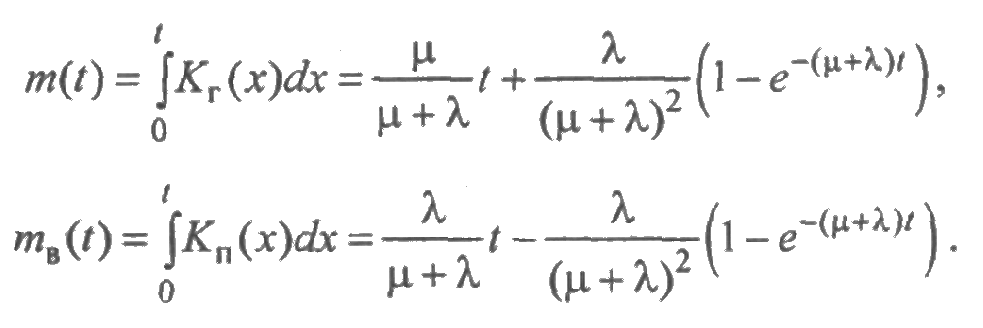
Приведенные соотношения будут часто использоваться в дальнейшем. Для распределений, отличных от экспоненциального (за редким исключением), не удается получить явных соотношений для рассмотренных показателей надежности.

4.2. Общая модель надежности систем в терминах интегральных уравнений

4.2.1«Основные обозначения и допущения

Предположим, что техническая система состоит из т элементов с известными распределениями времени безотказной работы и времени восстановления, а ее функционирование осуществляется в соответствии с заданной схемой расчета надежности. Все элементы условно разделим на рабочие и резервные. К первому классу отнесем также все элементы нагруженного и облегченного резерва, а ко второму — только элементы, находящиеся в ненагруженном состоянии. При отказе рабочего элемента и при наличии резервного он заменяется резервным, причем эта замена осуществляется мгновенно и абсолютно надежным устройством. Как будет показано в гл. 8, ограничение о мгновенной замене можно снять. При наличии нескольких резервных элементов порядок замены отказавшего рабочего элемента резервным будем считать известным. Контроль состояния элементов является непрерывным, и отказ любого элемента обнаруживается немедленно после его возникновения. Это условие также может быть снято (см. гл. 10). Предполагается, что число ремонтных бригад и порядок восстановления отказавших элементов известны, т. е. имеется указание о том, какие элементы и в какой последовательности будут приняты на обслуживание. Разумеется, этот порядок необходимо знать только в том случае, когда речь идет об ограниченном восстановлении и мо­жет появиться очередь на восстановление. Восстановление элемента начинается сразу же после его отказа или после обнаружения отказа контролирующим устройством при наличии свободной бригады или по очереди, согласно принятому приоритету обслуживания. В процессе ремонта элементов происходит полное восстановление их надежности.

На функционирование и на ремонт каждого элемента могут оказывать влияние остальные элементы системы. В связи с этим, любой элемент может пребывать в нескольких возможных состояниях: в состоянии работоспособности, в состоянии восстановления или в состоянии простоя. Причем состояние простоя элемента может быть обусловлено следующими причинами:

□ произошло прерывание работы элемента, что может быть в том случае, если данный элемент находится в составе узла, соединенного последовательно с отказавшим элементом или узлом;

□ произошло прерывание восстановления элемента, что может быть в том случае, когда дисциплина обслуживания системы такова, что ремонтные органы, восстанавливающие данный элемент, прекращают его восстановление и приступают к ремонту некоторого другого элемента (восстановление с приоритетом);

□элемент исправен, но по условиям функционирования он находится в очереди на работу, что может произойти, например, в случае ненагруженного резервирования;

□ элемент находится в отказовом состоянии, но по условиям обслуживания он не ремонтируется и находится в очереди на восстановление, что возможно, например, в случае ограниченного восстановления с прямым или назначенным приоритетом.

Указание возможных состояний каждого элемента системы существенно при описании ее функционирования в целом. Будем считать, что переход каждого элемента из одного состояния в другое осуществляется мгновенно вследствие отказа или восстановления данного элемента или какого-либо другого элемента системы. Дополнительно предложим, что отказ или восстановление любого элемента не влияет на законы распределения остальных элементов и время простоя элемента (если не оговорено особо) не сказывается на его характеристиках надежности, т. е., находясь в состоянии простоя, элемент сохраняет эти характеристики такими же, как и в момент прерывания работы или восстановления.

4.2.2. Матрица состояний

Множество всех состояний системы обозначим через Е, а через п — число этих состояний. В соответствии с заданным понятием отказа все состояния системы разбиваются на два класса: множество работоспособных состояний Е₊ и множество отказовых состояний Е_. В каждый фиксированный момент времени t и для каждого k-го состояния определяются шесть подмножеств множества всех элементов:

· R_k —множество номеров работающих элементов;

· W_k — множество номеров ремонтируемых элементов;

· R_k' — множество номеров элементов, находящихся в состоянии простоя вследствие прерывания их функционирования;

· W_k' — множество номеров элементов, находящихся в состоянии простоя вследствие прерывания их восстановления;

· R_k⁰ — множество номеров элементов, образующих очередь на работу;

· W_k⁰ — множество номеров элементов, образующих очередь на восстановление.

С каждым k-м состоянием (kϵЕ) свяжем вектор А_k = (а_1k, а_2k,..., а_mk), характеризующий состояния всех элементов системы в момент времени t. Компоненты вектора А_k предполагаются равными:

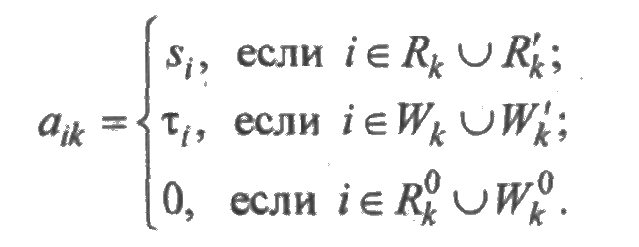
Если i ϵ R_k' (i ϵ W_k') то соответствующую компоненту будем иногда снабжать штрихом и писать s_i' (τ_i'). Если а_ik = 0, то соответствующую компоненту будем называть "нулевой" и для различия состояний будем писать а_ik = ОR, если 1-й элемент находится в очереди на работу, или а_ik = ОW, если i -и элемент находится в очереди на восстановление. "Нулевая" компонента должна содержать также четкое указание о порядковом номере очереди на работу или очереди на восстановление, если таких компонентов более одной. В некоторых случаях, когда это не может вызвать недоразумений, "нулевые" компоненты мы будем опускать.

Таким образом, функционирование любой восстанавливаемой системы полностью определяется матрицей состояний S размерности т×п, столбцами которой служат векторы А_k.

Для удобства матрица состояний дополняется верхней строкой, содержащей коды (или номера) соответствующих состояний, например совокупностью (упорядоченной или неупорядоченной) отказавших элементов, и нижней строкой, показывающей, к какому классу (Е₊ или Е_) относится состояние с номером k: 1, если k ϵ Е₊, или 0, если k ϵ Е_-.

Date: 2015-07-17; view: 893; Нарушение авторских прав