Описание функционирования системы с помощью уравнений

типа массового обслуживания

Составить систему дифференциальных уравнений типа массового обслуживания для определения количественных характеристик надежности восстанавливаемой системы можно по виду графа состояний системы.

Сформулируем первоначально правило составления уравнений для определения вероятности пребывания системы в i -м состоянии в момент времени t.

Часть произвольного графа с состояниями i -1, i, i +1 показана на рис. 5.10.

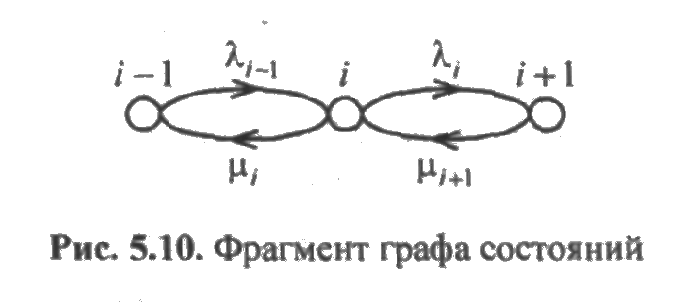
Дифференциальное уравнение для вероятности рi(t) пребывания системы в i -м состоянии в момент времени t будет иметь вид:

Из уравнения видно, что слева пишется производная по времени от вероятности пребывания системы в i -м состоянии в момент времени t, а справа - сумма произведений интенсивностей переходов из всех соседних состояний в i-е состояние и из i -го во все состояния на соответствующие вероятности состояний. Знаки в правой части уравнения определяются по направлению стрелок в ветвях графа. Если стрелка направлена в i -е состояние, то при соот­ветствующей интенсивности перехода ставится знак "+", в противном случае — знак "-". Это правило справедливо при любом числе соседних с i -м состояний.

ПРИМЕР 5.4. Составить систему дифференциальных уравнений, описывающих функционирование системы, граф состояний которой приведен на рис. 5.7, г.

Решение. На основании сформулированного правила и в соответствии с графом состояний система дифференциальных уравнений будет иметь вид:

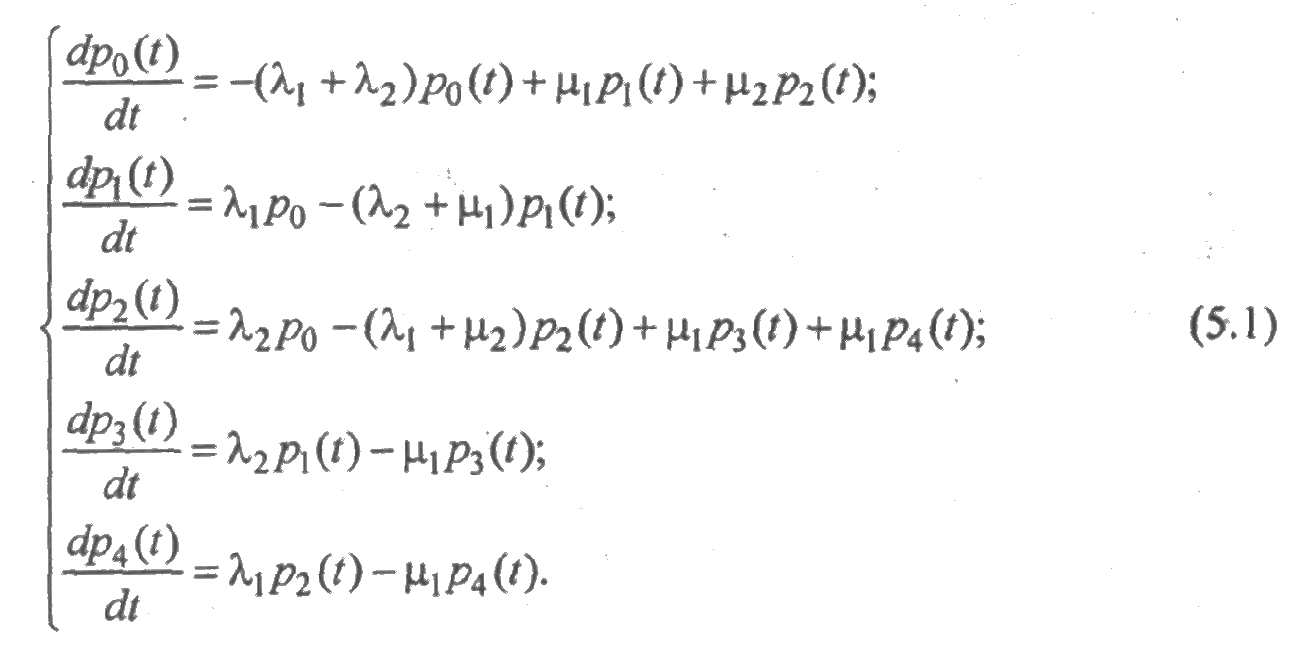
Написанные ранее уравнения позволяют найти вероятность того, что система в данный момент времени находится в i -м состоянии.

На практике часто приходится определять вероятность того, что в течение времени t система попадает в i -е состояние. Для определения этой вероятности необходимо считать i -е состояние поглощающим и запретить, путем постановки экранов, переходы из i -го состояния во все остальные. Преобразовав, таким образом, граф состояний, записываются дифференциальные уравнения по сформулированному выше правилу.

Для нашего случая состояния (3) и (4) являются отказовыми. Для определения вероятности безотказной работы дублированной системы запретим переход из состояния (3) в состояние (1), а также из состояния (4) в состояние (2). Тогда система (5.1) преобразуется в следующую систему дифференциальных уравнений:

Укажем на одно важное свойство уравнений функционирования системы. Так как сумма всех вероятностей состояний системы равна единице, т. е.

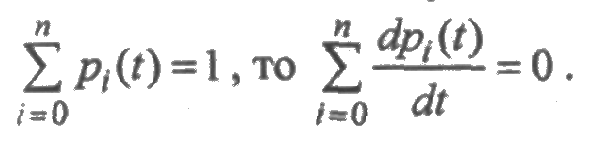
А это значит, что сумма правых частей системы уравнений всегда равна нулю.

Это свойство полезно иметь в виду при проверке правильности составления уравнений функционирования системы.

Дифференциальные уравнения типа массового обслуживания позволяют определить вероятности состояний системы или вероятности попадания в эти состояния в течение времени t. По известным вероятностям р_i(t) можно найти любую другую количественную характеристику надежности системы. А это означает, что система уравнений достаточно полно описывает функ­ционирование восстанавливаемой системы.

В установившемся режиме функционирования вероятности состояний являются величинами постоянными. Тогда все производные равны нулю и система дифференциальных уравнений превращается в систему линейных алгебраических уравнений.

Для случая, рассмотренного в примере 5.4, система дифференциальных уравнений (5.1) превращается в следующую систему алгебраических уравнений:

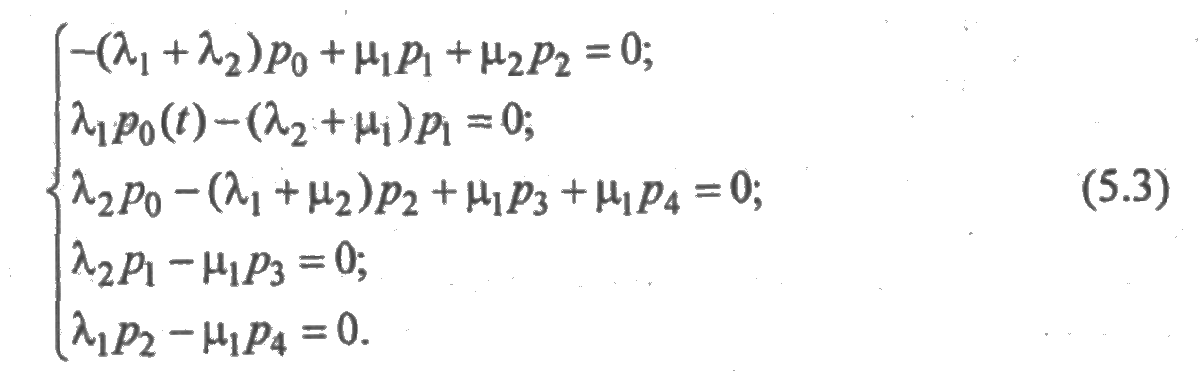
Эта система является однородной (ноль в правой части каждого уравнения) и имеет бесконечное множество решений. Для получения однозначного реше­ния системы следует использовать нормировочное уравнение

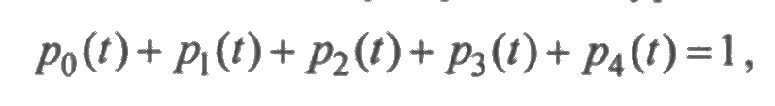
которым заменяется одно любое уравнение системы (5.3).

Анализ способов описания функционирования технических систем позволяет сделать ряд важных выводов.

Существуют, по крайней мере, следующие три способа описания функционирования восстанавливаемых систем:

□ схема расчета надежности (структура системы);

□ граф состояний;

□ система дифференциальных уравнений типа массового обслуживания.

Схема расчета надежности не позволяет в полной мере описать функционирование восстанавливаемой системы, т. к. она не дает возможности учесть дисциплину обслуживания отказавших элементов. Однако она является исходной для построения графа и для составления дифференциальных уравнений функционирования системы.

Описание функционирования восстанавливаемой системы с помощью графа состояний обладает высокой наглядностью. В этом основное преимущество данного способа перед всеми остальными. Граф состояний в ряде случаев дает возможность качественно сравнить различные схемные решения, выбрать наиболее приемлемую дисциплину обслуживания, наметить пути по­вышения надежности систем. Он существенно облегчает процедуру записи дифференциальных уравнений функционирования системы.

Граф состояний достаточно полно описывает функционирование восстанавливаемой системы. По графу состояний наиболее просто найти финальные вероятности пребывания системы в любом i -м состоянии, а также интегральные показатели надежности — наработку на отказ и среднее время восстановления системы. Он позволяет определить также показатели надежности невосстанавливаемых систем.

Функционирование восстанавливаемой системы можно наиболее полно описать системой дифференциальных уравнений. Решая уравнения известными в классической математике методами, можно вычислить любую количественную характеристику надежности. Наличие программ решения системы дифференциальных уравнений на ЭВМ существенно расширяет возможности метода. Однако описание функционирования восстанавливаемой системы с помощью дифференциальных уравнений имеет существенные недостатки.

Метод не обладает наглядностью и требует громоздких вычислений при определении количественных характеристик надежности даже сравнительно простых систем.

Сложные системы имеют большое число состояний (сотни и тысячи). Анализ надежности таких систем путем решения уравнений типа массового обслуживания практически невозможен.

Интенсивности отказов элементов в большинстве практических случаев не являются величинами постоянными. Имеет место старение элементов и, как следствие, λ_i(t)≠const. В таких случаях описание функционирования системы с помощью дифференциальных уравнений типа массового обслуживания невозможно. В этом основной недостаток метода дифференциальных уравнений.

На смену им приходит метод, который в теории надежности называется методом интегральных уравнений.

5.1.7. Описание функционирования системы с помощью интегральных уравнений

Описание функционирования системы с произвольными законами распределения времени до отказа и времени восстановления элементов состоит в следующем:

- определяются все состояния системы и переходы между состояниями;

- для каждого состояния определяется вектор состояний элементов системы;

- вводится неизвестная функция, соответствующая каждому состоянию системы;

- составляется система интегральных уравнений.

ПРИМЕР 5.5. Составить систему интегральных уравнений, описывающую функционирование системы, граф состояний которой приведен на рис. 5.7, г. Плотность распределения времени до отказа i -го элемента равна f_i(t), а плотность распределения времени восстановления i -го элемента — g_i(t). В момент времени t = 0 система считается полностью исправной.

Решение. Состояния системы и переходы между состояниями показаны на графе на рис. 5.7, г. Рассмотрим каждое состояние системы. В состоянии (0) оба элемента являются исправными, и этому состоянию соответствует вектор A ₀ = (s₁,s₂). Аргументы s₁ и s₂ означают, что, когда система пребывает в состоянии (0), оба элемента являются работоспособными. В состоянии (1) первый элемент восстанавливается, а второй работает. Этому состоянию соответствует вектор А₁ = (τ₁, s₂), в котором аргумент τ₁ соответствует восстановлению первого элемента. В состоянии (2) второй элемент восстанавливается, а первый работает. Этому состоянию соответствует вектор А₂ = (s₁, τ₂) в котором аргумент τ₂ соответствует восстановлению второго элемента. В состоянии (3) оба элемента являются не рабочими, причем согласно принятой дисциплине обслуживания первый элемент восстанавливается, а второй находится в очереди на восстановление. Этому состоянию соответствует вектор А₃ = (τ₁,0). Нулевой аргумент означает простой второго элемента в ожидании, пока не освободится ремонтная бригада, занятая восстановлением первого элемента. В состоянии (4) оба элемента также являются не рабочими. В силу принятой дисциплины обслуживания восстанавливается первый элемент, но при этом не было закончено восстановление второго элемента, и ремонтная бригада переключилась на восстановление первого элемента. Этому состоянию соответствует вектор А₄ = (τ₁, τ₂^’ ). Аргумент τ ₂^’ означает, что второй элемент восстанавливался, однако восстановление было прервано отказом первого элемента.

Указанные векторы поместим в матрицу состояний:

Верхняя строка матрицы содержит номера состояний системы, а нижняя строка состоит из нулей и единиц. Значение нижней строки равно 1, если соответствующее состояние системы является работоспособным, и 0, если состояние системы является отказовым.

Каждому i -му состоянию системы сопоставим неизвестную функцию у_i, аргументами которой служат компоненты i -го столбца матрицы S и время t:

Функция y₀ (s_1,s_2, t) плотность распределения вероятностей времени пребывания системы в момент t в состоянии (0) при условии, что после момента t первый элемент будет работать время s₁, а второй элемент — время s₂. Функция y₁ (τ_1,s_2, t) есть плотность распределения вероятностей времени пребыванш системы в момент t в состоянии (1) при условии, что после момента t первый элемент будет восстанавливаться время τ₁, а второй элемент будет работать в течение времени s₂. Функция y₂ (s_1,τ_2, t) есть плотность распределения вероятностей времени пребывания системы в момент t в состоянии (2) приусловии, что после момента t первый элемент будет работать время s₁, а второй элемент будет восстанавливаться в течение времени τ₂. Функция y₃ (τ₁,0, t) есть плотность распределения вероятностей времени пребывания системы в момент t в состоянии (3) при условии, что после момента t первый элемент будет восстанавливаться время τ₁. Функция y₄ (τ₁, τ₂^’, t) есть плотность распределения вероятностей времени пребывания системы в момент t в состоянии (4) при условии, что после момента t первый элемент будет восстанавливаться время τ₁, а остаточное время восстановления второго элемента равно τ₂^’. Таким образом, аргументы функций у_i характеризуют осстаточные времена работы или восстановления элементов.

На основании формулы (4.11) система интегральных уравнений будет иметь вид:

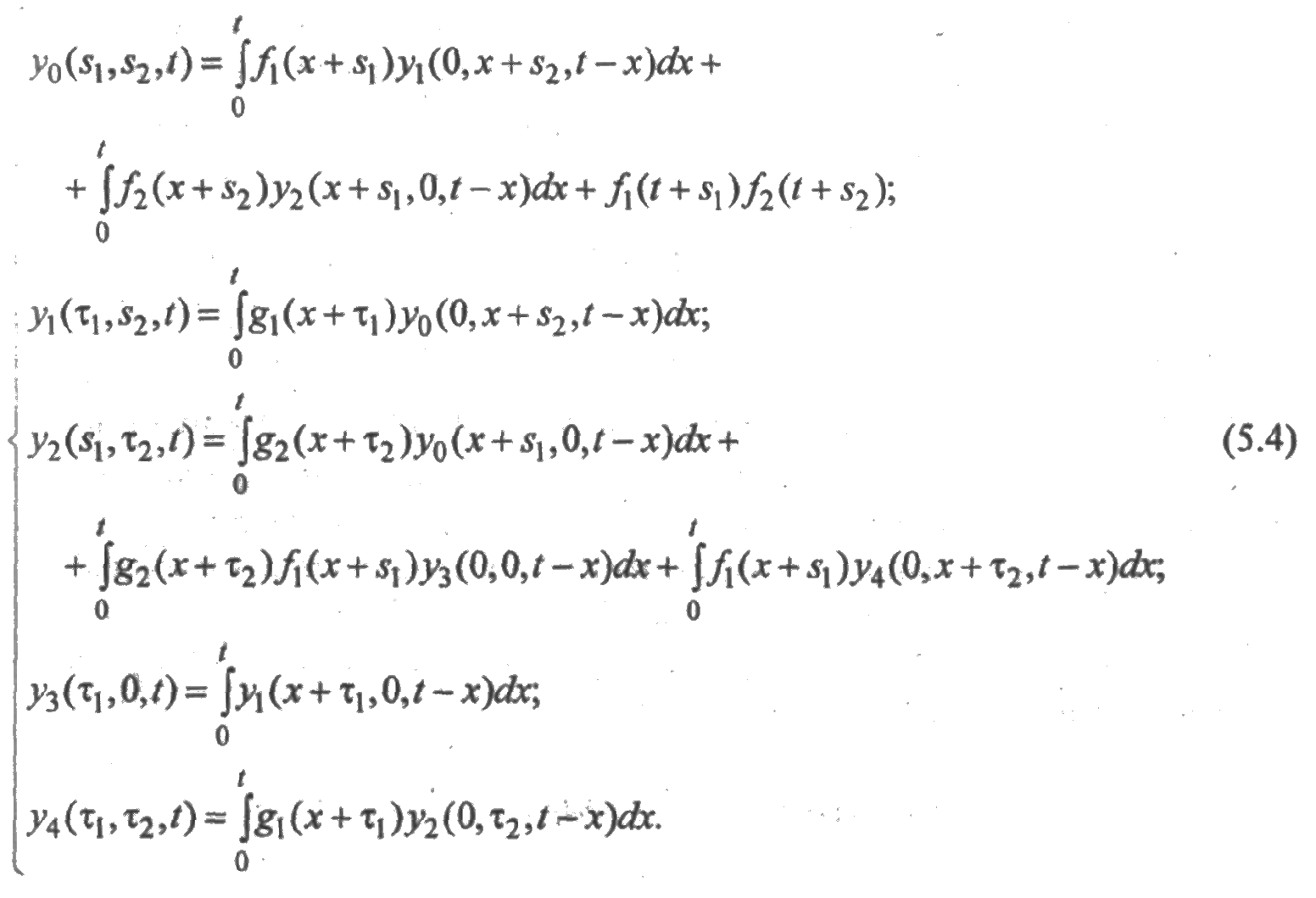
При составлении системы надо учитывать следующее: если аргумент s_i, или τ_i не содержит "штрих", то в правой части под знаком интеграла к такому аргументу добавляется переменная интегрирования; если в аргументах s_i, или τ_i имеется "штрих", то к данному аргументу переменная интегрирования не добавляется. После этого "штрихи" над аргументами могут быть опущены, как это сделано в последнем уравнении.

Решение данной системы уравнений позволяет найти вероятности пребывания системы в каждом состоянии, которые определяются интегрированием соответствующих функций по всем "ненулевым" аргументам:

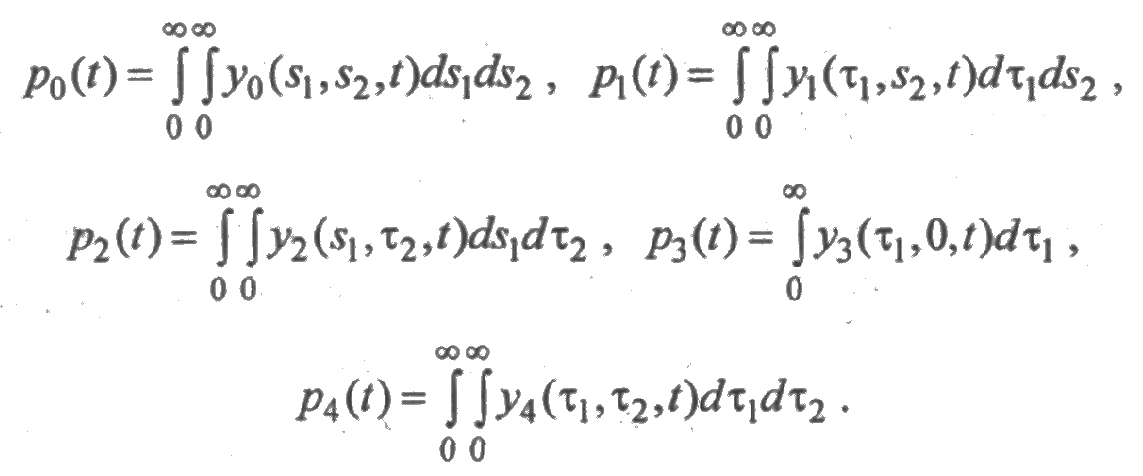
Решение системы интегральных уравнений позволяет найти также параметры перехода из одного состояния в другое. Чтобы найти параметр перехода из состояния i в состояние j, в функции у_i надо положить нулю аргумент, соответствующий элементу, который вызвал данный переход, и проинтегрировать функцию у_i по остальным аргументам. Например, параметр перехода из состояния (0) в состояние (1) равен а параметр перехода из состояния (3) в состояние (2) равен ω₃₂(t) = y₃ (0,0,t).

Здесь указан способ получения вероятностей р_i(t) того, что в момент времени t система будет находиться в состоянии i. Если нас интересует вероятность первого попадания системы в состояние i, то это состояние надо сделать поглощающим. Например, чтобы найти вероятность безотказной работы системы, запретим выходы из состояний (3) и (4). Тогда изменяются аргу­менты функций у₃ и у₄: y₃(τ₁^’, 0, t) y₄(τ₁^’, τ₂^’, t), а система интегральных уравнений преобразуется к виду:

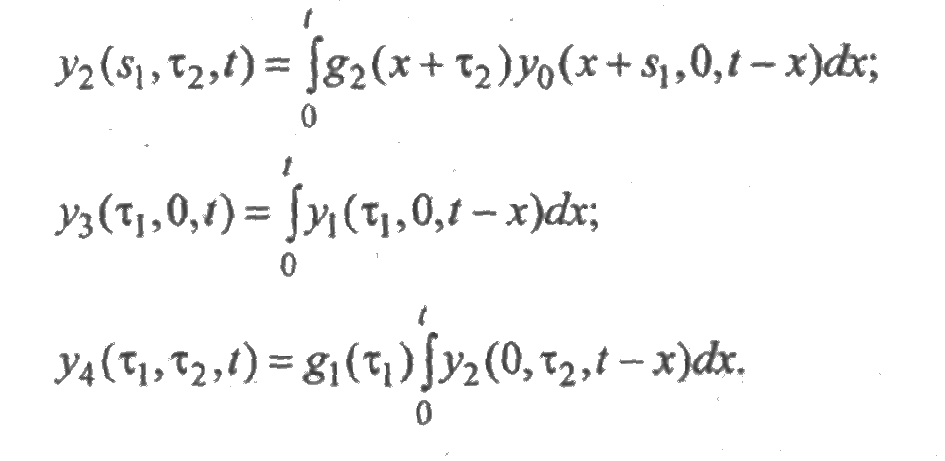
В результате решения данной системы и интегрирования функций у_i получим вероятности исправных состояний и вероятность безотказной работы системы в течение времени t:

P(t) = p₀(t)+p₁(t)+p₂(t).

По известным вероятностям p_i(t) и параметрам переходов ω_ij(t) можно найти любую другую количественную характеристику надежности системы. Это значит, что система интегральных уравнений полностью описывает функционирование восстанавливаемой системы с произвольными законами распределения.

В установившемся режиме функционирования система уравнений (5.4) упрощается незначительно и по-прежнему остается системой интегральных уравнений:

Вероятности состояний и параметры переходов вычисляются так же, как для нестационарного режима.

Система (5.6) имеет бесконечно много решений, и ее следует решать вместе с условием нормировки:

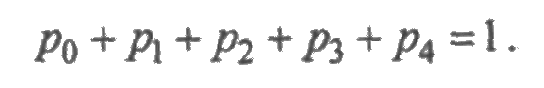
5.2. Методы анализа надежности технических систем, основанные

Date: 2015-07-17; view: 1094; Нарушение авторских прав