Научное обоснование критериев и показателей надежности

Не существует единственного критерия, достаточно полно характеризующего надежность сложной системы. Это объясняется ее многофункциональностью. От надежности сложной системы зависят такие ее показатели, как качество, эффективность, долговечность, готовность, безопасность, живучесть и риск. При этом для обеспечения высоких показателей необходимо, чтобы сложная система была высоконадежной и удовлетворяла требованиям по множеству критериев, таких как вероятность безотказной работы, среднее время безотказной работы, наработка на отказ, функция и коэффициент готовности и др.

Так, например, для достижения заданной эффективности системы необходимо гарантировать определенное значение вероятности безотказной работы, для обеспечения долговечности — среднее время безотказной работы, для обеспечения готовности — коэффициент готовности.

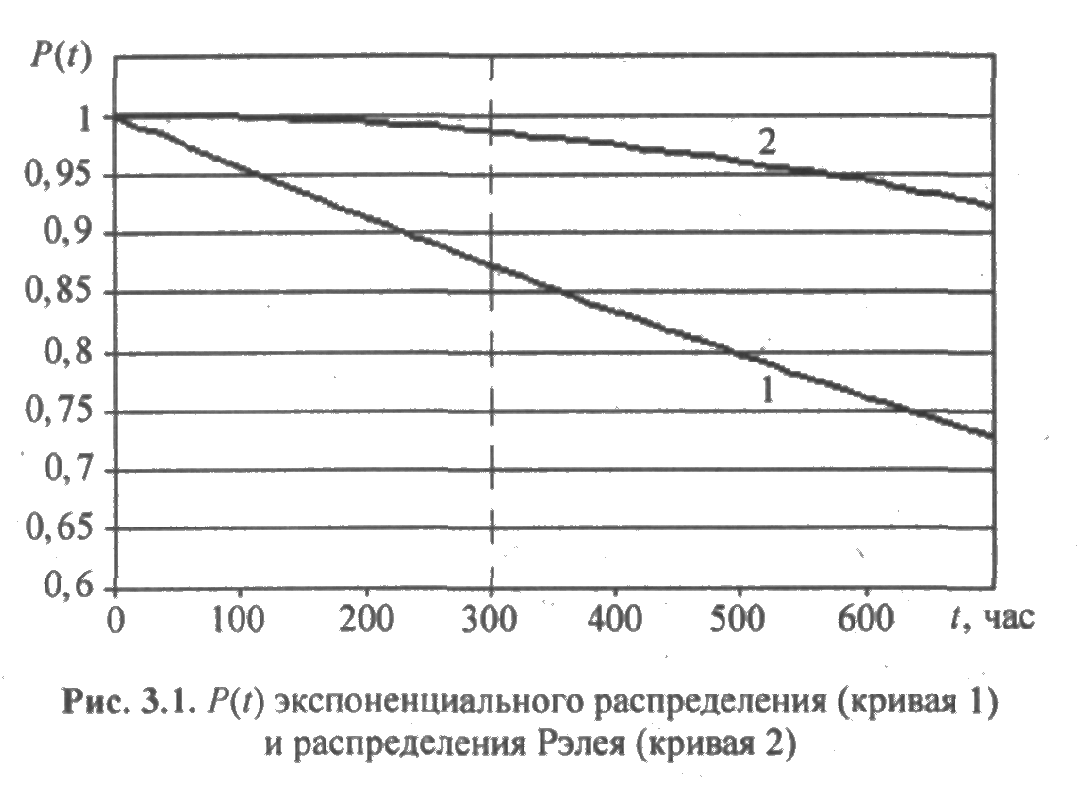
Между тем, все критерии надежности связаны между собой однозначными математическими зависимостями. Поэтому, задавая требования на множество критериев, в большинстве случаев обнаруживается их противоречивость и физическая нереализуемость. Например, для обеспечения эффективности сложной системы задается требование на вероятность безотказной работы Р(t) = 0,97 в течение 300 часов, а для обеспечения долговечности — нара­ботка на отказ T = 2200 час. Эти критерии связаны зависимостью т. е. при задании требований на Р(t) наработка на отказ уже будет однозначно определена. Например, если время до отказа системы имеет экспоненциальное распределение, то наработка на отказ не будет удовлетво­рять требуемому значению. Если время до отказа системы подчинено распределению Рэлея, то наработка на отказ соответствует заданному требованию на долговечность (рис. 3.1).

Техногенный риск системы R(t) вычисляется по формуле:

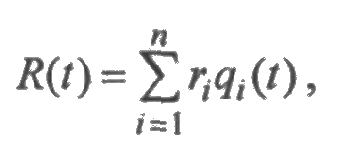
где r_i — риск при возникновении отказа i -го типа, q_i(t) — вероятность отказа i -го типа.

Из формулы видно, что для обеспечения заданного риска не обязательно иметь систему с высокой вероятностью безотказной работы Р(t). Достаточно, чтобы система имела высокую вероятность того, что не возникнут такие отказы, которые приводят к большому риску. Снова возникли противоречия в выборе показателей надежности с точки зрения эффективности и риска.

Следует также иметь в виду, что способы обеспечения надежности существенно зависят от критерия. Например, для обеспечения вероятности безотказной работы эффективным методом является структурное резервирование, а для обеспечения среднего времени безотказной работы системы длительного существования — нагрузочное резервирование. Какое же из них выбрать, если требования задаются одновременно на два критерия Р(t) и Т? Применение одновременно нескольких методов может привести к излишней избыточности, а значит, к повышению стоимости, веса и габаритов системы. Можно продолжать приводить примеры, однако сказанного достаточно, чтобы убедиться в противоречивости требований, задаваемых на показатели на­дежности с разных позиций.

Задачу выбора критериев и показателей надежности сложных систем можно сформулировать так: дана сложная система и требования на ее надежность в виде семейства критериев. Требуется определить набор критериев, который бы обеспечил все требования и одновременно не содержал противоречивых критериев. Решая эту проблему, исследователю придется во многих случаях формулировать новые критерии, т. к. задача в такой постановке является некорректной из-за однозначных зависимостей между существующими критериями. Такими обобщенными могут быть критерии вида:

где Z — обобщенный критерий надежности; R_i — i -й критерий; С_i — коэффициент значимости i -го критерия; k — число критериев, полностью характеризующих систему с точки зрения ее надежности.

3.2. Разработка моделей функционирования сложной системы

Разработанные в теории надежности модели функционирования сложных систем часто являются слишком абстрактными, а поэтому не адекватны оригиналам. Они не учитывают неодновременность работы элементов, наличие последействия отказов и естественной избыточности, физической реализуе­мости структурного резервирования, а также не обеспечивают требуемой точности расчетов.

Элементы сложной системы, являющейся многофункциональной, работают не одновременно. При этом набор элементов, одновременно функционирующих, существенно зависит от внешних факторов, а поэтому является величиной случайной. В моделях, реализованных на практике, в большинстве случаев не учитывается человек как активный элемент информационной системы. Анализ надежности таких систем требует моделирования собственного времени функционирования системы. В большинстве практических случаев вычисление показателей надежности осуществляется по формулам:

При этом интенсивность отказов системы равна сумме интенсивностей отказов ее элементов, т. е. Здесь не учитывается то обстоятельство, что число одновременно работающих элементов является функцией времени: n = f(t).

В резервированных структурах имеют место последействия отказов, т. к. отказ резервных элементов неизбежно приводит к увеличению интенсивностей отказов исправных элементов. Последействия имеют место также в ремонтируемых системах, потому что после ремонта показатели надежности элементов, подвергшихся ремонту, иные, чем до ремонта.

Применение резервирования на практике требует учета его физической реализуемости: наличия автоматов контроля и коммутации при резервировании замещением, наличия двух характеров отказов элементов электроники, изменения параметров элементов при раздельном резервировании с постоянно включенным резервом и т. д.

Неодновременность работы элементов и наличие последействия отказов являются основанием утверждать, что интенсивность отказов сложной системы не может быть величиной постоянной, если даже интенсивности отказов элементов постоянны. Отсюда вытекает важный вывод: экспоненциальный закон надежности к сложным системам не применим.

В сложных системах могут возникать внезапные, постепенные и перемежающиеся отказы. Существующие модели предполагают независимость этих отказов. Это допущение для случая сложных систем сомнительно. Изменение параметров системы по причине ее старения изменяет коэффициенты нагрузки, а значит, и вероятность возникновения внезапных отказов и сбоев.

К сложным системам предъявляются высокие требования надежности. Необходимо, например, чтобы вероятность безотказной работы или коэффициент готовности имели значение несколько девяток после запятой. Между тем, интенсивности отказов элементов, получаемые из эксплуатации, содержат, как правило, только одну или две значащие цифры. Тогда расчеты показателей надежности, выполняемые в процессе проектирования, принципиально не могут иметь значения большие, чем одна или две цифры после запятой. Из сказанного ранее можно сделать следующий важный вывод: разработка математических моделей функционирования сложных систем является математической и технической проблемой; ее решение следует искать в разработке приближенных моделей и методов их реализации, учитывающих необходимость моделирования собственного времени системы, наличие последействия отказов, физическую реализуемость системы, обеспечение погрешностей расчета.

Существующие модели, в частности экспоненциальная, позволяют выполнить лишь сравнительную оценку надежности различных схемных решений выбрать наилучшую. Они практически не дают возможности с необходимой для практики точностью получить ответ в виде числа.

Проблема анализа надежности столь сложна, что возникает мысль отказаться от численных показателей надежности и разработать показатели качественные. При наличии качественных показателей расчеты не требуются. Такие показатели должны быть научно обоснованы, при этом они будут уникальными для данной системы. Эта проблема будет обсуждаться в гл. 14.

В следующих пунктах настоящей главы подробно рассматриваются проблемы анализа надежности технических систем. Дается обзор существующих методов, их возможности, достоинства и недостатки. Главное внимание уделяется вопросам анализа надежности сложных систем при не экспоненциальных законах распределения отказов и восстановлений.

3.3. Методы анализа надежности технических систем

3.3.1. Обзор существующих методов расчета надежности сложных систем

Анализ надежности технических систем производится, как правило, на основе известных методов с привлечением данных об отказах и восстановлениях элементов, полученных в результате эксплуатации или испытаний систем и их элементов. На практике обычно используют аналитические методы, а также Методы имитационного и статистического моделирования. Математический аппарат теории надежности сложных систем состоит из большого числа аналитических методов. Прежде всего, это логико-вероятностные методы, методы, основанные на теории случайных процессов, декомпозиции, асимптотические и эвристические, аналитико-статистические.

Основой аналитических методов для решения задач надежности служит теория случайных процессов (марковских, полумарковских, многомерных марковских). При помощи однородных марковских процессов с конечным или счетным множеством состояний [20,26,28,45] описывается эволюция систем при максимальных ограничениях: время безотказной работы, восстановления и подключения резервных элементов, временной резерв, время между. сеансами контроля, проведения контроля, существования скрытых отказов и т. д. Они не должны зависеть от предшествующей истории, а значит, имеют экспоненциальные распределения.

Экспоненциальные законы распределения можно использовать только в том случае, когда потоки отказов и восстановлений являются простейшими, т. е. обладают свойствами ординарности, стационарности и отсутствия последействия. Вообще говоря, потоки отказов элементов технических систем можно считать ординарными. Потоки восстановлений могут быть неординарными, когда одновременно восстанавливаются несколько элементов. Свойство стационарности должно быть подвергнуто сомнению, т. к. в системе возможно старение или омоложение элементов, и за равные промежутки времени вероятности появления тех или иных событий могут быть различны. Наличие последействия проявляется постоянно, например, после любого ремонта или любого отказа резервированного элемента.

Случайные процессы, с которыми приходится встречаться в теории надежности, далеко выходят за пределы марковских процессов. Попытка отказаться от предположения об "экспоненциальностн" отказа или восстановления хотя бы одного элемента приводит к появлению значительных трудностей в связи с необходимостью составлять системы ннтегродифференциальных уравнений. Эти уравнения в теории массового обслуживания впервые рассматривались Р. Форте, Д. Коксом, Б. А. Севастьяновым [102] для простейшего входящего потока и произвольного распределения длительности обслуживания заявок. Ю. К. Беляев [13] ввел в рассмотрение класс линейчатых марковских процессов, составил для них интегродифференциальные уравнения и использовал их для решения некоторых задач теории надежности.

Математическое описание функционирования системы с произвольными распределениями (Эрланга, нормальное и т. д.) часто удается получить с помощью теории полумарковских процессов, когда процессы исправной работ: и обслуживания рассматриваются в специально подобранные моменты времени [13,34,41, 59,60,64] или марковскими процессами восстановления со специально построенным фазовым пространством [55, 56, 93]. Эти приемы использовал еще А. Я. Хинчин, а позднее Д. Кендалл. Однако поведение сложной системы с восстановлением лишь в нескольких исключительных и довольно тривиальных случаях удается описать полумарковским процессом. Для расширения круга решаемых задач применяются процессы с вложенными точками, которые также используются для оценки надежности достаточно простых восстанавливаемых систем. Методы, основанные на полумарковских процессах, применяются в тех случаях, когда только некоторые распределения (часто одно или небольшое их количество) являются произвольными, а остальные — экспоненциальными. Кроме того, эти методы, как правило, позволяют определять лишь стационарные значения показателей надежности, а для исследования переходных процессов функционирования системы здесь возникают непреодолимые трудности. Возможности применения методов ограничены, поскольку в общем виде на их основе не удается разработать математическую модель восстанавливаемой технической системы с учетом структурной избыточности и любой дисциплины ремонта.

Известно [25], что любой случайный процесс может быть дополнен до марковского соответствующим расширением фазового пространства. Следуя этому теоретическому положению, в настоящее время выполнен анализ надежности класса систем, описываемых суперпозицией независимых полумарковских процессов [65, 105]. Основные недостатки этих работ— невозможность исследования более сложных зависимых процессов и известные трудности в исследовании нестационарных характеристик.

В более общих ситуациях приходится рассматривать марковские процессы с континуальным множеством состояний, т. е. многомерные марковские процессы [45, 53, 56]. На их основе удается описать эволюцию технической системы при произвольных распределениях времен безотказной работы и восстановления элементов с учетом структурной и временной избыточности, учетом контроля технических средств, с учетом нескольких видов отказов и т. д. Инженерная реализация метода многомерных марковских процессов в простейших случаях осуществляется с помощью статистического моделированияна ЭВМ, требующего колоссальных затрат машинного времени и памяти. Даже ускоренные методы статистических испытаний часто не позволяют произвести расчет надежности с требуемой точностью в реальном масштабе времени.

Среднее время восстановления элементов технических систем обычно в несколько раз меньше среднего времени между соседними отказами. Это обстоятельство позволяет использовать для оценки их надежности асимптотические методы. Исследование надежности систем с помощью асимптотических методов является важной задачей, т. к. точные формулы для характеристик надежности удается получить лишь в редких случаях, и они, как правило, сложны для практического использования. Распределения исходных характеристик элементов обычно заранее не известны, а их оценка требует большего труда, чем оценка некоторых числовых параметров.

В практическом плане интерес представляют результаты, в которых доказывается асимптотическая независимость показателей надежности от исходных распределений. Примером могут служить исследования А. Д. Соловьева и Б. В. Гнеденко [7], в которых установлено, что распределение длительности безотказной работы резервированных систем в условиях "быстрого" восстановления асимптотически экспоненциально. Асимптотический анализ сложных систем, основанных на сочетании аналитического метода и метода статистического моделирования, проводился в работах И.Н. Коваленко, 3.А. Ивницкого, Н. М. Акулиничева [52, 53, 54].

В настоящее время работы, посвященные изучению свойств восстанавливаемых систем на основе асимптотического метода, носят в основном теоретический характер и могут использоваться для систем с малым числом состояний. Эти методы не определяют предельное значение параметра, начиная с которого можно использовать асимптотические формулы. С помощью этих методов затруднен также анализ переходных процессов. И, наконец, погрешность характеристик надежности может быть достаточно высокой.

Перечисленные методы имеют наибольшее распространение в практике инженерных расчетов. Тем не менее, для анализа надежности систем с неэкспоненциальными распределениями иногда применяются и другие методы. Это, прежде всего, методы логико-вероятностные, графовые, укрупнения состояний, эвристические, аналитико-статистические, декомпозиции, разложения на фазы, диффузионных процессов, Кендалла и метод аппроксимации интенсивностей.

Логико-вероятностные методы основаны на непосредственном применении теорем теории вероятностей для анализа надежности технических систем. Дифференциальный метод разложения на фазы, а также метод Кендалла, применяемый в задачах массового обслуживания с одним пуассоновским случайным процессом, позволяют сводить немарковскую модель к марковской. Практически эти методы позволяют использовать лишь распределения Эрланга и приводят к значительному увеличению числа состояний. Подобные трудности встречаются при оценке надежности систем с большим числом равнонадежных элементов методом диффузионных процессов, как непрерывного аналога уравнений Колмогорова. Эти методы могут использоваться для расчета стационарных характеристик надежности и вероятности безотказной работы для систем кратковременного действия. При этом "неэкспоненциальные" компоненты, как правило, состоят из нескольких фаз и имеют распределение Эрланга. С помощью введения промежуточных состояний, соответствующих моментам окончания фаз, модель сводится к марковской. Методы ступенчатой аппроксимации интенсивностей отказов и восстановлений элементов можно применять для оценки надежности систем, имеющих незначительное число состояний и медленно изменяющиеся интенсивности. Определение погрешностей расчетов на основе этих методов — сложная задача.

Более общей для описания технической системы является графовая модель, учитывающая влияние практически любых факторов, влияющих на систему, например средств контроля и системы обслуживания. Существенным недостатком описания системы графом состояний является сложность ввода данных и методов определения характеристик надежности, если количество состояний системы велико. Здесь могут использоваться методы укрупнения состояний [59] с недостатками, присущими методам полумарковских процессов.

Сущность эвристического метода оценки надежности восстанавливаемых систем состоит в объединении групп элементов этой системы в одни эквивалентный элемент, который характеризуется альтернирующим процессом восстановления. Тем самым происходит уменьшение числа элементов в системе. Метод применяется исключительно для случая высоконадежных элементов и систем и не позволяет установить погрешность вычислений.

Метод декомпозиции сложных систем основан на построении оценочных математических моделей, позволяющих получать простые и достаточно точные верхнюю и нижнюю границы для оцениваемого показателя надежности. Основные сложности метода связаны с его точностью.

Методы машинного моделирования в целом являются универсальными и допускают рассмотрение систем с большим количеством элементов [21,29,53, 144]. Однако их использование в качестве метода исследования задач надежности целесообразно лишь тогда, когда трудно или невозможно получить аналитическое решение. Основными этапами такого исследования являются: построение формальной модели, разработка программ имитации траекторий модели, проведение имитационных экспериментов.

При анализе высоконадежных систем с помощью имитационной модели возникают проблемы, связанные с очень большими затратами машинного времени, необходимого для вычислений с требуемой точностью. Для увеличения скорости расчетов применяются методы ускоренного моделирования, искусственного введения моментов регенерации, "взвешенного" моделирования, в частности метод малого параметра, а также комбинированные методы анализа с приложениями методов статистического моделирования. С увеличением надежности элементов эффективность моделирования уменьшается [52, 54], и оно становится практически не реализуемым. Часто используется методика уменьшения дисперсии, которая базируется на применении дополнительной информации относительно системы [132,144]. Однако этот метод не может быть использован для разработки универсальных прикладных программ оценки надежности. Здесь проявляется противоречие между основными требованиями, предъявляемыми к математическим моделям, а именно: с требованиями адекватности и универсальности с одной стороны и высокой экономичности с другой. Методы статистического и имитационного модели­рования не позволяют в полном объеме определять надежность системы, если учесть большое количество сопутствующих факторов, влияющих на ее функционирование. Поэтому следует подчеркнуть исключительную важность проведения исследований по надежности систем аналитическими методами [7].

3.3.2. Причины неэкспоненциальности случайных параметров, отказов и восстановлений технических систем

В настоящее время большинство практических расчетов в области надежности предполагает использование экспоненциального закона распределения времени между отказами элементов и параметров функционирования системы, таких как время принятия решения, время перерыва в работе элементов, время существования скрытого отказа и т. д. Это обусловлено, с одной стороны, известным положением о сходимости суммарных независимых потоков отказов к пуассоновскому потоку и, с другой стороны, сравнительной простотой аналитических расчетов. Известно, однако, что использование экспоненциального закона, как правило, приводит к существенному расхождению аналитических и экспериментальных данных о надежности сложных систем.

Если не учитывать неэкспоненциальность распределений времени безотказной работы и времени восстановления элементов сложной системы, то это может привести к чрезвычайно большим ошибкам [97,108,109].

Элементы электроники, как правило, имеют экспоненциальное распределение времени безотказной работы. Однако устройства, содержащие непоследовательно соединенные в смысле надежности элементы, уже не обладают экспоненциальными распределениями. Поэтому включение этих устройств в систему в качестве ее элементов приводит к необходимости исследовать надежность системы при неэкспоненциальных распределениях.

Покажем, что при нагруженном резерве вероятность безотказной работы устройства подчиняется гиперэкспоненциальному распределению, а при ненагруженном или смешанном резервировании — обобщенному гамма-распределению.

Экспоненциальное распределение обладает следующим свойством: свертка (см. разд. 2.5) плотностей есть плотность, подчиненная обобщенному гамма-распределению, причем если все λ_i, различны, то свертка указанных плотностей дает гиперэкспоненциальное распределение. Действительно, свертка всех плотностей f_i(t) с одинаковыми параметрами λ_i обра­зует плотность гамма-распределения, а свертка гамма-распределений с разными параметрами, как известно, приводит к плотности обобщенного гамма-распределения. В частности, если все λ_i различны, то имеем линейную комбинацию плотностей экспоненциальных распределений:

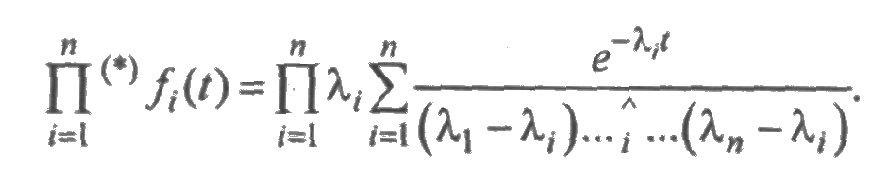
Функционирование невосстанавливаемого устройства, элементы которого имеют экспоненциальные распределения, описывается графом состояний, в ветви которого проставлены параметры этих распределений. На рис. 3.2 приведен фрагмент графа, содержащий вершину i ₀, предшествующую ей вершину i _-1, и вершины i ₁, i₂,..., i _k, следующие из данной вершины за один пере ход.

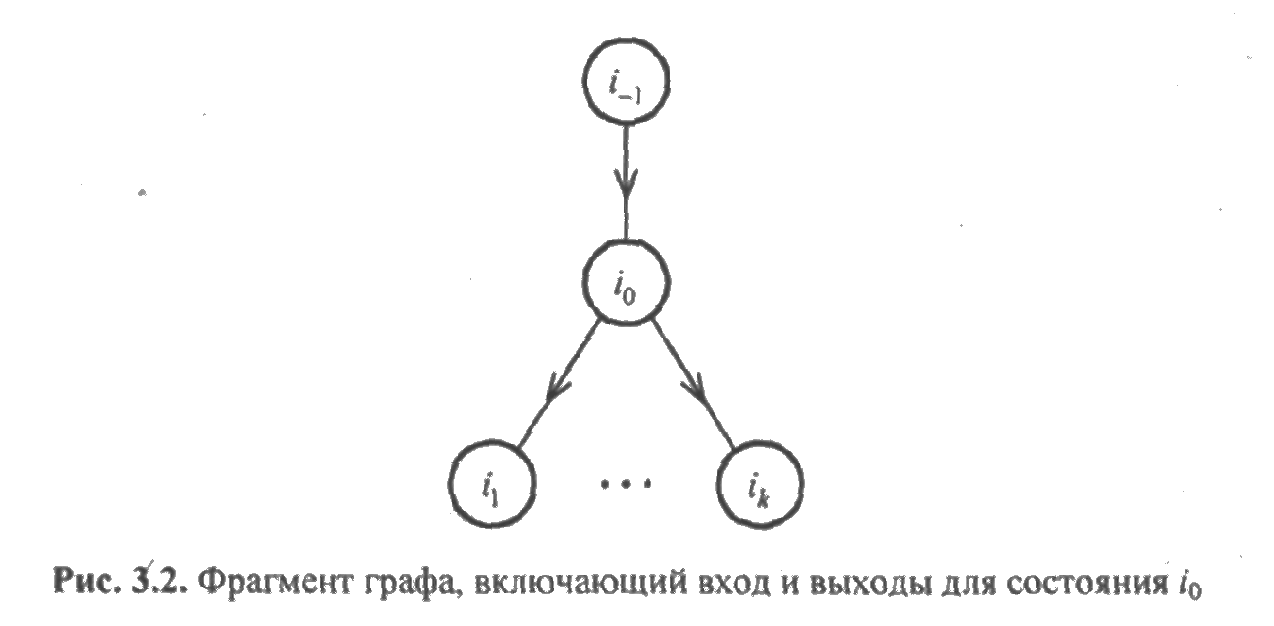
Тогда для вероятности р_i0 (t) состояния i₀ справедливо равенство

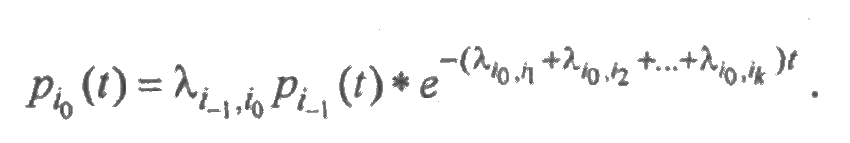
Это значит, что вероятность пребывания системы в любом состоянии равна свертке экспоненциальных функций, и, в силу сделанного ранее замечания, она представляет собой линейную комбинацию гамма-распределений. Отсюда следует, что вероятность безотказной работы также равна линейной комбинации гамма-распределений.

Заметим, что эта линейная комбинация гамма-распределений превращается в линейную комбинацию экспоненциальных распределений, если все суммарные интенсивности переходов для любого пути графа различны. Поскольку для основного соединения и нагруженного резерва суммарная интенсивность при переходе на более низкий уровень графа убывает, то плотность распределения времени безотказной работы всей системы имеет гиперэкспоненциальное распределение. Ненагруженное и скользящее резервирование отмеченным свойством не обладает, а поэтому плотность распределения времени безотказной работы системы имеет обобщенное гамма-распределение. Подобные заключения можно сделать и для элемента с экспоненциально распределенным резервом времени, и для элементов, обладающих экспоненциальным распределением, но в которых учитываются дополнительные свойства, такие как возможность накопления нарушений, встроенный контроль, два вида отказов и др.

Еще в большей степени это относится к механическим элементам, которые принципиально являются стареющими. Как показывают проводимые исследования [8,105], время безотказной работы механических элементов имеет распределение Вейбулла или усеченное нормальное распре­деление. Значит, экспоненциальная модель не адекватна физическим процессам, протекающим в системе. Для ремонтируемых систем время восстановления практически никогда не является экспоненциальным, т.к. оно складывается из времени обнаружения, времени локализации и времени устранения неисправности, т. е. равно сумме (зависимых или независимых) обычно не­экспоненциальных распределений случайных величин. Причинами неэкспоненциальных распределений также могут быть: неодновременность работы элементов, наличие восстановления большого числа механических устройств, наличие искусственной и естественной избыточности.

Таким образом, проблема анализа надежности восстанавливаемых систем с произвольными распределениями отказов и восстановления является не только научной, но главным образом технической проблемой, вытекающей из свойств сложных систем.

3.3.3. Зависимость показателей надежности от законов распределения и дисциплины восстановления элементов

В теории надежности важное место отводится нахождению простых приближенных расчетных формул для показателей надежности. В то же время эти формулы должны иметь достаточно высокую точность, удовлетворяющую инженера-практика. Как показывают исследования, даже в случае простейших резервированных систем не удаётся найти простых аналитических соотношений для вычисления показателей надежности с требуемой точностью. Исключение составляют некоторые системы специального вида, показатели надежности которых зависят только от математических ожиданий времени безотказной работы и времени восстановления элементов и не зависят от законов распределения. Так бывает, например, в следующих случаях:

-элементы системы независимы по отказам и восстановлению (параллельное соединение с неограниченным восстановлением);

- при вычислении стационарных показателей надежности, когда отсутствует очередь на работу исправных элементов и очередь на восстановление отказавших элементов системы.

Однако при вычислении показателей надежности, как правило, недостаточно знать лишь первые моменты соответствующих распределений. Если даже предположить, что среднее время восстановления элементов значительно меньше среднего времени их исправной работы, то и в этом случае существующие расчетные формулы дают весьма грубые приближения к истинным значениям показателей надежности. При надлежащем выборе законов распределения относительная погрешность может быть очень высокой и даже неограниченной. Кроме того, эти формулы не учитывают приоритета обслуживания отказавших элементов. Как известно, для экспоненциальных распределений дисциплина восстановления элементов незначительно влияет на показатели надежности всей системы, особенно если ее функционирование протекает при дополнительном условии "быстрого" восстановления. Однако если законы распределения неэкспоненциальны, то дисциплина восстановления может оказать существенное влияние на надежность системы. В этом можно убедиться на примерах некоторых резервированных систем.

ПРИМЕР 3.1. Дано: восстанавливаемая дублированная система, составленная из равнонадежных элементов с ограниченным восстановлением. Оценить влияние дисциплины восстановления элементов на среднюю наработку на отказ системы.

Решение. Предположим, что время безотказной работы элементов экспоненциальное с параметром λ, а время восстановления имеет произвольное распределение с плотностью g(t)/ В гл. 7 будет показано, что средняя наработка на отказ для прямого, обратного и назначенного приоритетов выражается формулами:

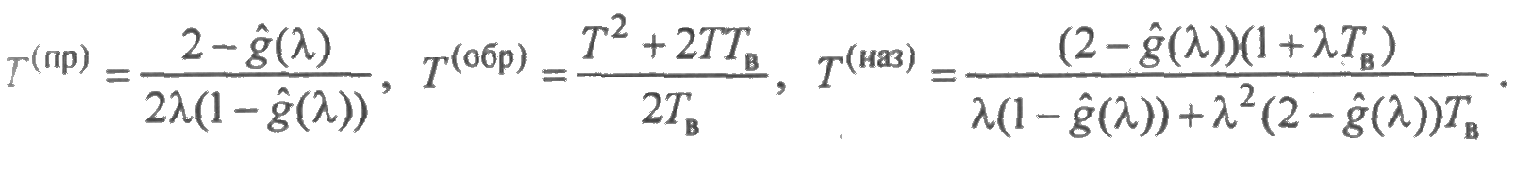
Здесь и далее — преобразование Лапласа (см. разд. 2.5) функции g(t), T_в — среднее время восстановления элементов. Предположим, что g(t)=cμe^-μt + (1-c)νe^-νt и имеет место "быстрое" восстановление элементов, например: Т = 100 час, Т _в=1 час. Тогда λ= 0,01 час^-1, Путем простых преобразований легко показать, что Т ^(пр) →∞, если μ →0, ν →∞, тогда как Т^(обр)=5100 час. Например, полагая μ = 0,001 час^-1, ν = 10, получим Т ^(пр) = 27 577 час, Т ^(наз) = 8565 час. Таким образом, средняя наработка на отказ системы существенно зависит от приоритета обслуживания элементов. Сопоставим полученные результаты с асимптотической формулой справедливой при условии "быстрого" восстановления элементов и любой дисциплины восстановления. Видим, что Т^(ас) = 5000 час и существенно отличается от ее точного значения. Следовательно, простота асимптотических формул не может служить основанием для возможности их применения при оценке надежности резервированных систем.

ПРИМЕР 3.2. Дано: восстанавливаемая дублированная система из равнонадежных элементов, обслуживаемая одним ремонтным органом с прямым приоритетом. Установить зависимость среднего времени восстановления системы от закона распределения времени восстановления ее элементов.

Решение. Пусть распределение времени безотказной работы каждого элемента экспоненциальное с параметром λ, а время восстановления имеет гамма-распределение с плотностью средним Т _в= αβ и вероятностыо невосстановления

Тогда среднее время восстановления системы может быть найдено по формуле (см. гл. 7)

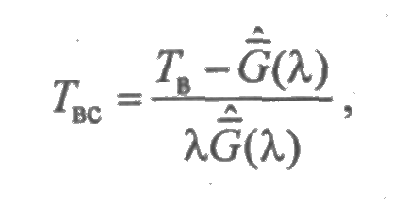
и, значит,

Исследуя это отношение в зависимости от α, получим графики, представлен­ные на рис. 3.3.

Таким образом, в зависимости от параметра α, а в общем случае — от закона распределения, можно получить характеристики надежности системы, изменяющиеся в достаточно широком диапазоне. При α = 1 имеем экспоненциальный случай, при котором Т_вс=Т_в.

Для неэкспоненциальных распределений некоторые показатели надежности не полно характеризуют систему и нечувствительны к ее изменениям.

ПРИМЕР 3.3. Дано: невосстанавливаемая резервированная система при общем резервировании с кратностью т- 1. Определить выигрыш в надежности G_T=T_c/T₀ для распределений: экспоненциальное, Вейбулла, вырожденное, равномерное.

Решение. Пусть — вероятность безотказной работы, а T ₀ — наработка до отказа одного элемента. Тогда для системы вероятность безотказной работы и средняя наработка до отказа вычисляются соответственно по формулам

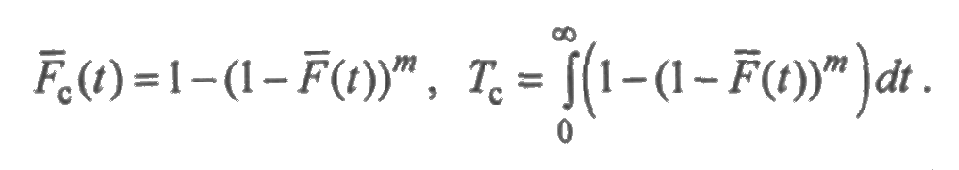
Для вырожденного распределения очевидно, что T_с = T₀ для любых значений т. Для распределения Вейбулла имеем

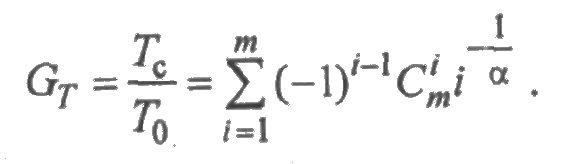
В частности, при α = 1 получаем экспоненциальное распределение, для которого

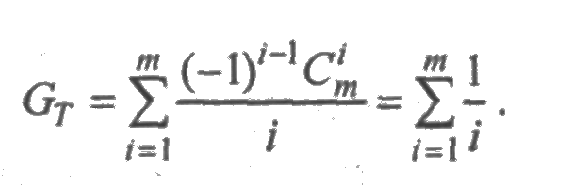
Для равномерного распределения с параметрами а и b

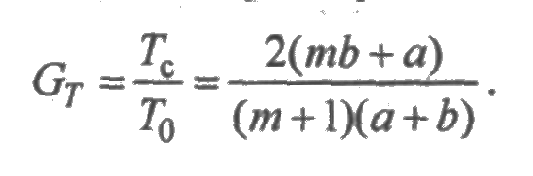
В частности, при а = 0 получим G_T=2m/m+1. Результаты расчетов по приведенным формулам сведем в табл. 3.1.

Как следует из таблицы, для вырожденного распределения наработка до отказа Т_с совершенно не чувствительна к числу резервных элементов. Для равномерного распределения резервирование также дает незначительный выигрыш (не более чем вдвое). Распределение Вейбулла при достаточно большом значении параметра α не оказывает существенного влияния с ростом т на изменение наработки до отказа. В то же время для распределения Вейбулла при молодеющем распределении можно получить любой сколь угодно большой выигрыш. Заметим, что для ненагруженного резерва G_T есть величина постоянная, равная т.

Приведенные примеры доказывают необходимость количественной оценки надежности систем при распределениях, отличных от экспоненциальных: она продиктована существенной зависимостью показателей надежности от законов распределения и дисциплины восстановления отказавших элементов.

3.3.4. Критичное влияние произвольных распределений отказов и восстановлений на нестационарные показатели надежности

Практические задачи, возникающие в теории надежности, показывают важность расчета и анализа нестационарных характеристик, которые часто не принимаются во внимание, хотя, как показывают вычислительные эксперименты, продолжительность переходного процесса может быть довольно большой. Более того, существуют системы, стационарное состояние которых вообще не наступает.

Пусть f(t) и g(t) — плотности распределения времени безотказной работы и времени восстановления элемента. Как было показано в разд. 2.6.1, функция готовности системы удовлетворяет уравнению

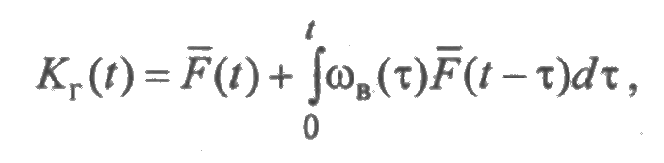
где функция ω_в, находится из уравнения

Численное решение этих уравнений для многих распределений не представляет затруднений. Получим аналитические выражения функции готовности для некоторых часто встречающихся распределений.

В преобразовании Лапласа выражение функции готовности имеет вид:

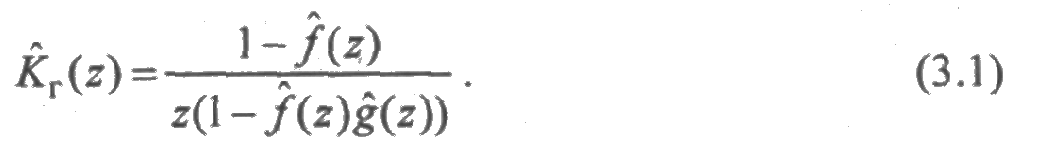
Случай 1. Если законы распределения экспоненциальные с параметрами λ и μ, то, как известно,

Случай 2. Закон распределения времени безотказной работы экспоненциальный, а времени восстановления — Эрланга 2-го порядка с параметром μ. Из (3.1) следует, что

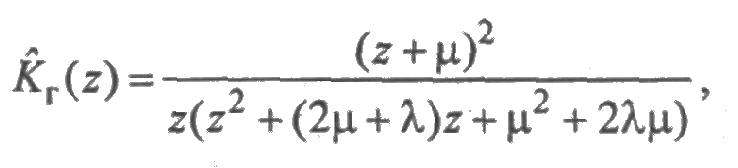
и функция готовности находится в явном виде:

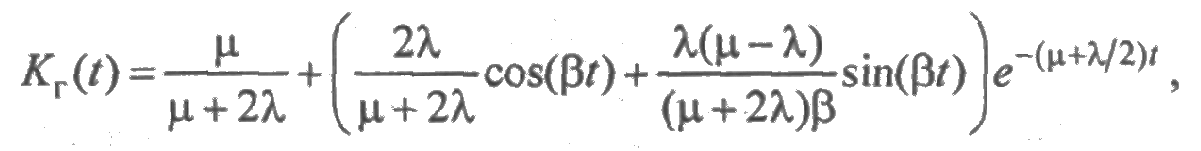
где при μ >λ/4. Точки экстремума b_к получаются в результате решения уравнения: Тем самым

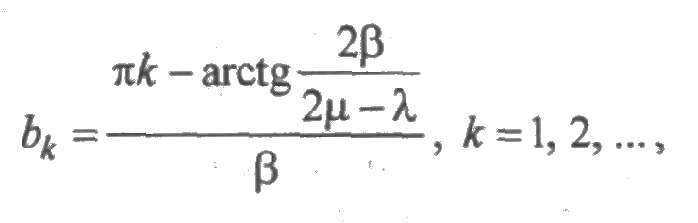
и функция K_г(t) имеет бесконечное число точек экстремума, а это соответствует колебательному процессу. Для значения b₁, имеем

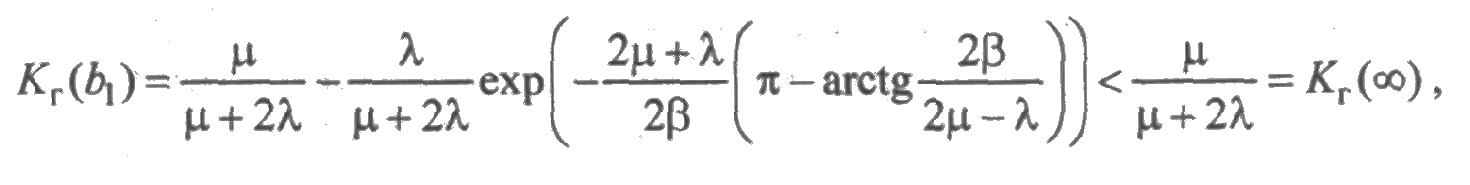
т. е. b₁ — точка минимума, в которой график функции готовности лежит ниже стационарного значения К_г. Значения a _k, в которых график функции готовности пересекает линию К_г(t) = К_г, определяются из уравнения

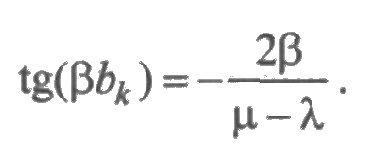
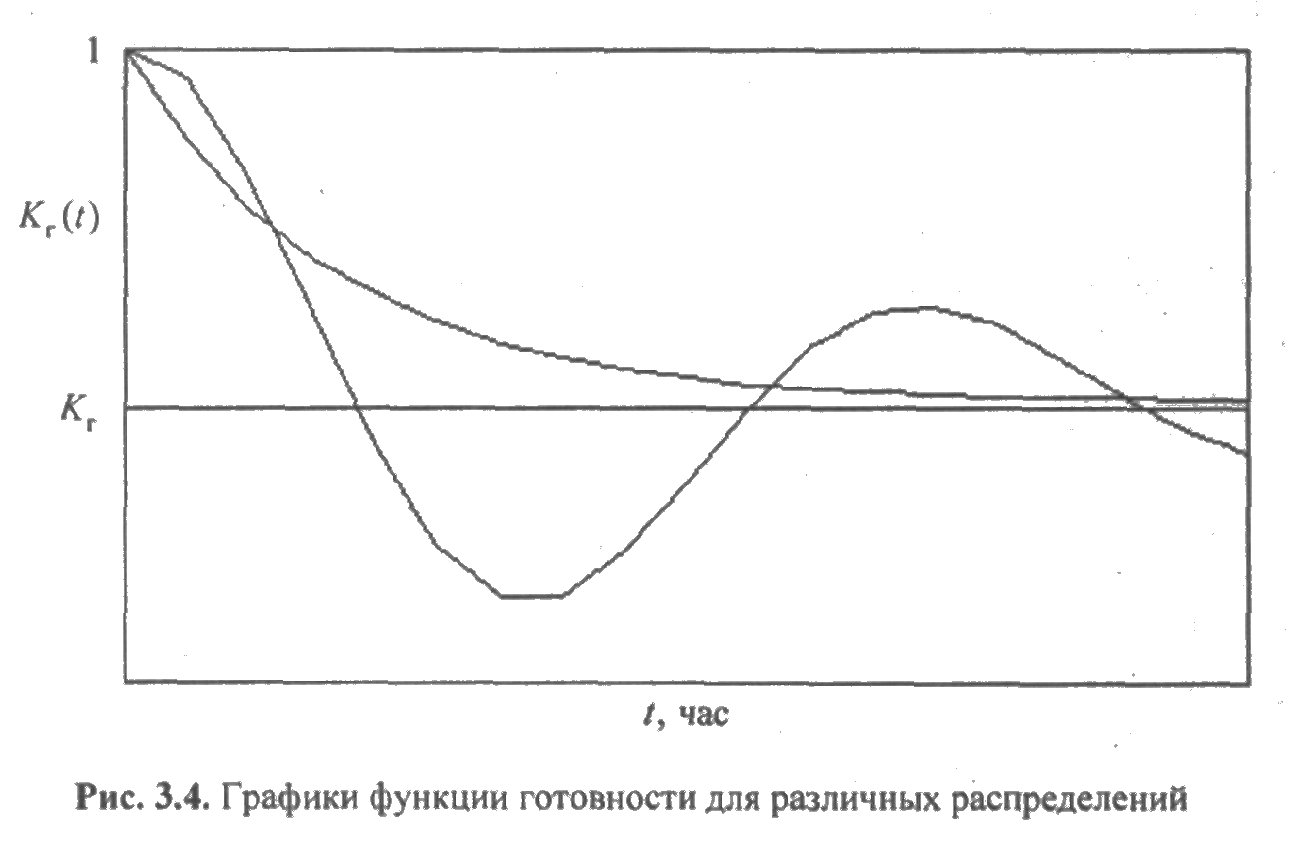
Это доказывает, что для произвольных распределений могут наблюдаться провалы функции готовности ниже ее стационарного значения. Графики функций готовности для 1-го и 2-го случаев приведены на рис. 3.4.

Для равномерного распределения с параметрами а и b преобразование Лапласа функции готовности имеет вид:

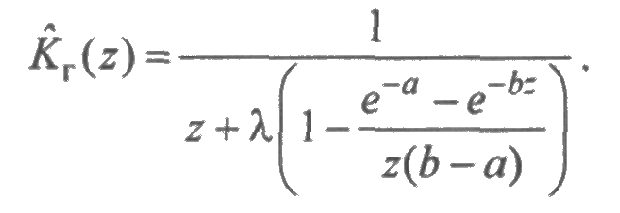
В этом случае в явном виде найти функцию готовности не удается. Тем не менее, расчеты, выполненные на ЭВМ, показывают достаточную близость функций готовности для равномерного распределения и распределения Эрланга. Таким образом, в отличие от экспоненциального случая, когда функция готовности всегда является монотонно убывающей, в общем случае функция готовности часто имеет колебательный характер. Поэтому может оказаться, что готовность системы для небольшого времени эксплуатации меньше, чем при ее длительной эксплуатации. Этот факт часто игнорируется на практике, что может привести к нежелательным результатам.

Можно показать, что с уменьшением дисперсии времен безотказной работы элементов усиливается колебательный характер функции К_г(t) и значительно увеличивается время наступления стационарного режима системы.

Случай 3. Законы распределения вырожденные со средними Т и Т _в, соответственно. В этом случае из (3.1) получим:

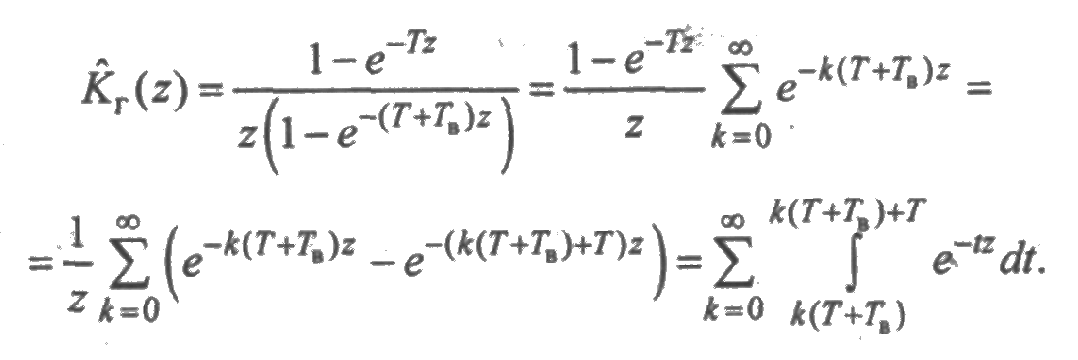
Из этого выражения следует, что функция К_г(t) тождественно равна единице на интервалах [k(Т + T _в), k(Т + T _в) + Т], k = 0,1, 2,..., и равна нулю вне этих интервалов, т.е.

График функции готовности приведен на рис. 3.5.

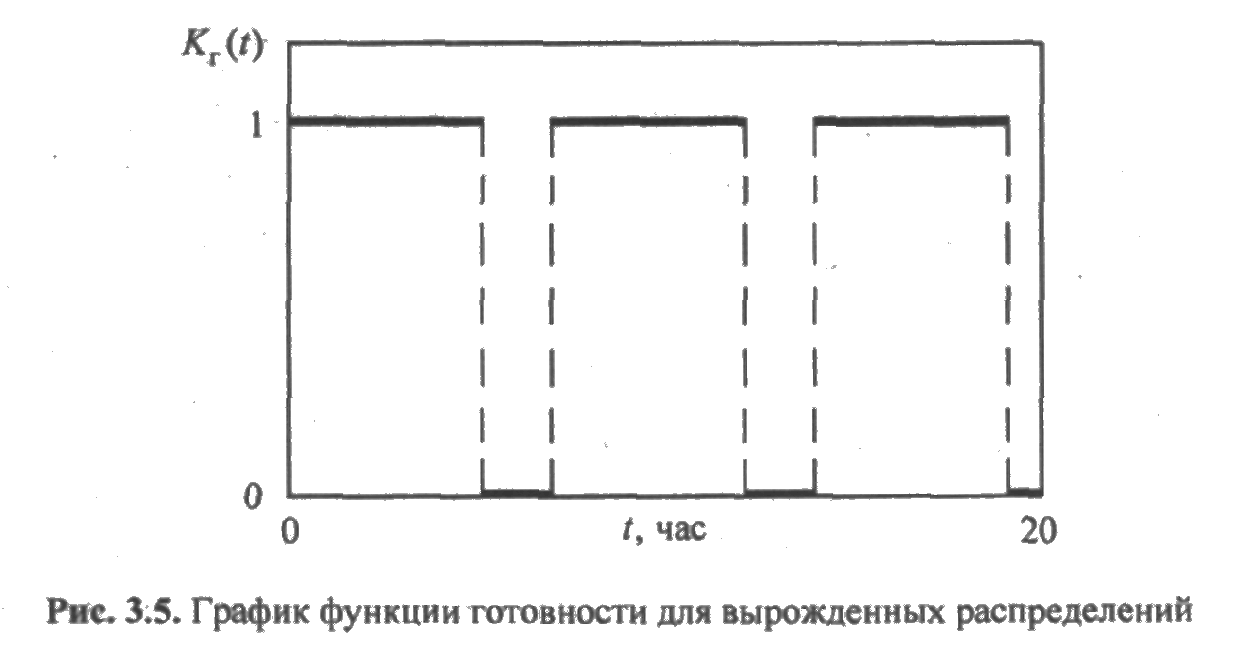
Стационарный режим здесь вообще не наступает, и коэффициент готовности не существует.

3.3.5. Методы и проблемы расчета надежности систем с большим числом состояний

При разработке математической модели технической системы с большим числом состояний, как правило, сталкиваются со следующими препятствиями, существенно затрудняющими анализ ее надежности:

□ неоднозначность понятия отказа системы;

□ взаимовлияние отказов элементов и частей системы;

□ неопределенность исходных данных;

□ многокритериальность;

□ восстанавливаемость;

□ наличие избыточности (естественной иди искусственной, введенной с целью повышения надежности);

□ наличие контроля состояний;

□ возможность перестройки структуры системы.

Одной из центральных проблем теории надежности больших систем следует считать разработку математического аппарата для ее расчета, анализа и прогнозирования. Сложность технической системы и большое число состояний ее функционирования приводит к необходимости решения систем уравнений весьма больших размерностей. Так, например, в системе из п элементов различной надежности с нагруженным резервом, обслуживаемой одним ремонтником, насчитывается состояний, где — число размещений из п по i. Даже для простейших схем (типа дублированной системы элементов) могут быть сотни состояний, если учитывать контроль состояний, переключение на резерв и другие особенности реальной системы.

В настоящее время для анализа надежности больших систем, как правило, используется общеизвестный математический аппарат, основанный на методах имитационного моделирования, асимптотического анализа, случайных процессов и связанных с ними интегродифференциальных уравнений. На основе этих методов расчеты характеристик надежности больших систем, обла­дающих значительной сложностью, достаточно редко могут быть доведены до численных результатов с требуемой точностью. Таким образом, отсутствие традиционных методов для анализа сложных технических систем с большим числом возможных состояний (порядка сотен тысяч и более) требует разработки нестандартных подходов к оценке их надежности и эффектив­ности. При рассмотрении надежности технических устройств обычно предполагается, что они могут пребывать в двух возможных состояниях: работоспособном и отказовом. Значение любого показателя надежности зависит от того смысла, которое вкладывается в понятие " отказовое " состояние. Исследование сложных систем ставит перед теорией надежности новые задачи. Если для исследуемой сложной системы определено понятие отказа, то принципиально можно найти требуемые характеристики надежности. Однако далеко не всегда очевидно, какое состояние системы можно считать отказовым. При появлении отказов отдельных частей лишь частично ухудшаются характеристики системы, но она продолжает выполнять свои функции. Возникает вопрос об оценке меры целесообразности применения данной системы.

В существующих методах расчета надежности технических систем обычно предполагается, что отказы элементов независимы, и система попадает в состояние отказа при отказе определенного числа элементов. Для сложных систем эти допущения часто бывают неприемлемыми. Между характеристиками отдельных частей системы имеется тесная взаимосвязь, и отказы отдельных частей системы являются зависимыми событиями. Возникает проблема изу­чения суммарных потоков отказов элементов большой системы и учета их влияния на надежность системы в целом.

В вопросах анализа надежности сложных систем с большим числом состояний существенным препятствием служит неопределенность начальных исходных данных по надежности и ремонтопригодности элементов. Как правило, характеристики времен безотказной работы и восстановления элементов являются случайными величинами, имеющими некоторые распределения вероятностей. Одной из особенностей моделирования сложной системы является также учет неопределенности данных.

3.3.6. Проблемы расчета надежности реконфигурируемых систем

Особой спецификой обладают системы с переменной структурой. В общем случае к ним можно отнести системы, характеристики надежности которых изменяются, например, из-за изменения нагрузки на систему или ее элементы, модификации структуры системы, наличия временных интервалов простоя элементов системы, изменения условий функционирования системы и т.д.

Указанные технические системы относятся к системам с реконфигурацией их структуры. Модификации в системе могут происходить как через постоянные, так и через переменные промежутки времени; они могут быть детерминированными или случайными, периодическими и непериодическими. Структура системы может изменяться потому, что меняются функции, вы­полняемые системой, а также с целью повышения ее надежности. Большое количество технических систем может быть интерпретировано как системы с модификациями или с переменной структурой [139].

Например, многопроцессорные системы могут изменять свою структуру в зависимости от исходных данных. То же относится и к производственным линиям, узлы которых могут выполнять различные операции в зависимости от условий их применения. Анализ подобных систем показывает, что, как правило, их модификации являются периодическими. Например, период для производственных линий может быть равен 24 часам или продолжительности производства цикла. Все модификации происходят в фиксированные моменты времени, между которыми характеристики надежности не меняются.

Анализ надежности систем со статической и динамической реконфигурацией структуры представляет собой новое направление в теории надежности сложных технических систем. Различаются системы, когда в момент изменения структуры информация о времени работы или восстановления элементов "забывается", и после момента реконфигурации система с измененной структурой начинает функционировать как новая. Это условие может быть вполне естественным для системы типа "черного ящика", о которой лишь известно, что она имеет два состояния и определены законы распределения вероятностей перехода между состояниями. Для таких систем предполагается, что допустимыми являются лишь переходы между исправными состояниями и ме­жду отказовыми состояниями. Иначе обстоит дело с системой, имеющей несколько уровней возможных состояний, а в процессе перестройки структуры системы имеются переходы между состояниями одного уровня. При этом может оказаться, что из исправного состояния система переходит в отказовое и, наоборот, из о тказового — в исправное. Таким свойством как раз обладают системы типа т/п с нагруженным и ненагруженным резервом.

Сложная техническая система с позиций надежности характеризуется такой специфической особенностью функционирования, как многофункциональность. Количество выполняемых системой функций может достигать нескольких десятков. При этом в реализации одной функции может участвовать большое число модулей (элементов). Один и тот же модуль может быть за­действован в выполнении нескольких функций. Поэтому модули, образующие систему, имеют различную длительность эксплуатации. Так, некоторые из них работают непрерывно, поскольку участвуют в выполнении всех функций, а некоторые модули включаются только на время выполнения какой-либо одной или нескольких функций. Многофункциональность накладывает определенный отпечаток на саму постановку задачи анализа надежности такой системы.

При изучении надежности систем, выполняющих несколько функций, как правило, применяется функциональный подход, при котором описание надежности производится по каждой функции в отдельности, а поэтому надежность системы характеризуется вектором показателей надежности всех ее функций. Таким образом, сравнительная оценка различных систем одного и того же назначения часто является затруднительной, а то и вовсе невыполнимой. Основной сложностью в исследовании многофункциональных систем, на наш взгляд, является то обстоятельство, что исследования проводятся без учета потока задач, поступающих в систему. В этом случае анализ надежности системы, функционирующей по нескольким функциям, неоднозначен, а возникающая при этом неопределенность без какой-либо дополнительной информации не поддается измерению. Выходом из этой тупиковой ситуации может служить исследование системы вместе с потоком задач, поступающих на обслуживание. Без учета потока задач можно говорить о временах использования системы по каждой функции и исследовать ее надежность с учетом времени выполнения системой всех ее функций.

Основным вопросом анализа систем с переменной структурой является разработка моделей и методов расчета характеристик их надежности, а также управление процессом модификаций с целью получения наибольшей надежности систем в соответствии с выбранными критериями.

Date: 2015-07-17; view: 1824; Нарушение авторских прав