Лемма Неймана-Пирсона

Рассмотрим вероятностную модель состоящую из двух распределений Р₀ Р₁ с общим носителем и функциями плотности и , . По выборке проверяется простая гипотеза Н₀: выборка взята из распределения Р₀ при простой альтернативе Н₁: выборке соответствует распределение Р₁. Определим критическую функцию как индикаторную функцию критической области.

Статистика L называется статистикой отношения правдоподобия, а критерий - критерием отношения правдоподобия или критерием Неймана-Пирсона.

Критерий отвергает нулевую гипотезу, если правдоподобие альтернативы функции в С раз превосходит правдоподобие нулевой гипотезы . Этот критерий обладает следующими замечательными свойствами.

Теорема 8.1. Критерий отношения правдоподобия является наиболее мощным критерием в классе всех критериев проверки простой гипотезы при простой альтернативе, размер которых не превосходит размера критерия . Если критерий имеет размер , то он обладает наибольшей мощностью в классе всех критериев уровня .

Доказательство

Пусть - любой другой критерий, размер которого

. (1)

Требуется показать, что тогда критерий 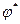имеет большую мощность чем критерий , то есть .

Рассмотрим интеграл .

Достаточно показать, что этот интеграл не отрицательный, и тогда первое утверждение теоремы будет следовать из неравенства:

, которая влечет (см. (1))

.

Покажем, что функции и произведение которых интегрируется., одновременно положительны или отрицательны при любых 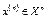. Действительно, если , то это влечет 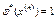, поскольку критическая функция равна единице, если она не равна нулю. Но по определению критерия отношения правдоподобия, равенство 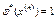возможно лишь в случае когда . Точно так же устанавливается, что неравенство 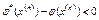влечет .

И так, критерий наиболее мощен в классе всех критериев, размер которых не превосходит размера . Если же , то это утверждение очевидно влечет его наибольшую мощность в классе всех критериев уровня .

Пример. Нормальное распределение. , ,

Мат. ожидания одинаковы и равны нулю.

Это неравенство соответствует следующему, исходя из предположения, что (в противном случае знак неравенства нужно менять)

Если вектор попал в сферу радиуса , то принимаем гипотезу

Х_i получены распределением

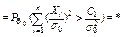
Если , то

(Хи квадрат с n-степенями свободы)

Плотность распределения X²_n

Зная находим в таблице распределения c_т² Кn(a)

- ошибка первого рода.

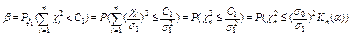- ошибка второго рода.

В этих двух примерах нам не нужна была сама выборка , а только функция от нее ()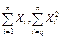

Пример. Биномиальное распределение.

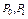
-вероятность получить выборку если было использовано распределение

0,1 вероятность получить этот вектор для 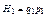, q₁ число нулей, p₁ число единиц.

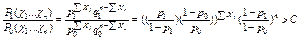
Пусть >

, - const для данной выборки

Если бы , то знак был бы на оборот.

т.к. число единиц в должно быть больше

Вариант 1: Считать суммы для разных .

Вариант 2:

,

графики

При увеличении n аргумент Ф будет стремиться к , то есть ошибка второго рода будет уменьшаться.

Вопрос.

Если N(a₀,1), N(a₁,1), то критическая область выглядела бы следующим образом

Если , то критическая область имела вид

Если то как будет выглядеть критическая область????J

Алгебра

Вопрос 2.1. Определение группы, примеры. Циклические группы и их свойства.

Опр. Пусть G – множество. Бинарной операцией на мн-ве G наз. однозначное отображение j:G*G®G

Опр. Группоид (G, j) – мн-во с заданной на нем бинарной операцией.

Опр. Пусть (G,*) – группоид. Операция * наз. коммутативной (абелевой), если для любых g,h Î G выполняется g*h=h*g.

Опр. Пусть (G,*) – группоид. Операция * наз. ассоциативной, если для любых a,b,c Î G выполняется a*(b*c)=(a*b)*c.

Опр. Ассоциативный группоид наз. полугруппой.

Опр. Пусть (G,*) – группоид. Нейтральным элементом группоида (G,*) наз. e Î G: e*g=g*e=g для любого g Î G.

Опр. Пусть (G,*) – группоид и существует нейтральный элемент е. Тогда g Î G наз. обратным к h Î G, если g*h=h*g=e.

Опр. Группоид (G,*) наз. группой, если:

a) существует нейтральный элемент

b) операция * ассоциативна

c) для любого элемента g Î G существует обратный

Опр. Подгруппой группы G наз. подмн-во H мн-ва G само являющееся группой.

Опр. Пусть M подмн-во G, (G,*)- группа. Тогда подгруппой группы G, порожденной модмн-вом M, наз. пересечение всех подгрупп гркппы G, содержащих М.

Опр. Тривиальными подгруппами являются группа е и группа G.

Опр. Нетривиальная подгруппа наз. собственной.

Опр. Группа, порожденная одним элементом, наз. циклической.

Опр. Порядком конечной группы явлю число элементов в ней. Обозначение .

Опр. Пусть (G,*) – группа, g Î G. Порядком элемента g наз. минимальное натуральное n: , если оно существует, или бесконечность в противном случае.

Теорема. Порядок элемента группы совпадает с порядком порожденной им циклической подгруппы. = ord g.

Д-во:

{ =e, , …}

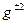1. Пусть ord g = 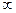, тогда , ... – все различные Þ <g> бесконечная группа.

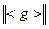2. Пусть ord g = n. Тогда е, , ... , =е, , ... То есть Þ <g>= { е, , ... } Þ =n.

Пример циклической группы: ()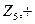

Date: 2016-08-30; view: 601; Нарушение авторских прав