Вопрос 9.1. Определение группы, примеры. Симметрическая группа подстановок. Теорема Кели. Системы образующих симметрической и знакопеременной групп.

Опр. Пусть G – множество. Бинарной операцией на мн-ве G наз. однозначное отображение j:G*G®G

Опр. Группоид (G, j) – мн-во с заданной на нем бинарной операцией.

Опр. Пусть (G,*) – группоид. Операция * наз. коммутативной (абелевой), если для любых g,h Î G выполняется g*h=h*g.

Опр. Пусть (G,*) – группоид. Операция * наз. ассоциативной, если для любых a,b,c Î G выполняется a*(b*c)=(a*b)*c.

Опр. Ассоциативный группоид наз. полугруппой.

Опр. Пусть (G,*) – группоид. Нейтральным элементом группоида (G,*) наз. e Î G: e*g=g*e=g для любого g Î G.

Опр. Пусть (G,*) – группоид и существует нейтральный элемент е. Тогда g Î G наз. обратным к h Î G, если g*h=h*g=e.

Опр. Группоид (G,*) наз. группой, если:

a) существует нейтральный элемент

b) операция * ассоциативна

c) для любого элемента g Î G существует обратный

Опр. Подгруппой группы G наз. подмн-во H мн-ва G само являющееся группой.

Опр. Пусть M подмн-во G, (G,*)- группа. Тогда подгруппой группы G, порожденной модмн-вом M, наз. пересечение всех подгрупп гркппы G, содержащих М.

Опр. Тривиальными подгруппами являются группа е и группа G.

Опр. Нетривиальная подгруппа наз. собственной.

Опр. Подгруппы группы S(W) наз. группами подстановок мн-ва W, а любая подгруппа группы Sn наз. группой подстановок степени n.

Пример:

Теорема Кели. Произвольная группа (G,*) изоморфна некоторой подгруппе группы (S(G),*).

Д-во: Поставим в соответствие каждому элементу gÎG отображение 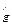: G®G, определяемое условием: для любого x ÎG 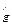(x)=xg.

Покажем, что 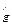Î S(G). Действительно, 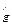- сюрьективно, так как для любого y ÎG выполняется 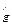(y )=y;

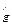- инъективно, так как для любых x, y ÎG выполняется 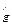(x)= 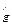(y) Û xg=yg Ûx=y.

Таким образом 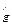= - подстановка на G.

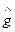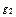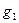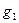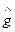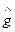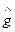Теперь покажем, что отображение y:G®S(G), определяемое правилом: для любого gÎG y(g)= - есть мономорфизм. Это отображение инъективно, так как если y()=y() для любых , ÎG, то = , то тогда = (е)= (е)= . Наконец, y - гомоморфизм группы (G,*) в группу (S(G),*), так как для любых h,g ÎG и любого x ÎG справедливы соотношения y(gh)= , (x)=xgh=(xg)h= (x)h= (x)=( )(x),

Доказывающие равентсво y(gh)= y(g) y(h).

Итак y - мономорфизм G в S(G) и следовательно y(G) подгруппа группы S(G), изоморфная G.

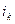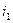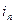Опр. Говорят, что числа , в перестановке s=( … )образуют инверсию, если большее из них расположено левее меньшего, то есть если 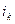< и k>l, то есть инверсия.

Опр. Перестановку наз. четной если она содержит четное число инверсий, и нечетной в противном случае.

Опр. Подстановку g= ÎSn наз. четной, если перестановка (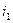 … 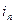) четная, и нечетной в противном случае.

Опр. Преобразование перестановки, заключающееся в перемене местами каких-либо двух ее элементов, наз. транспозицией.

Опр. Транспозицией в Sn наз любой цикл длины 2.

Опр. Подгруппу An всех четных подстановок группы Sn наз. знакопеременной группой подстановок степени n.

Теорема. Группа Sn порождается:

1. множеством всех транспозиций

2. множеством всех транспозиций вида (1,а) a Î

3. множеством всех транспозиций вида (a,a+1) a Î

4. транспозицией (1,2) и полным циклом (1,2,...,n).

Теорема. Знакопеременная группа An степени n 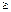3 порождается всеми циклами длины 3.

Date: 2016-08-30; view: 729; Нарушение авторских прав