Математические ожидания и дисперсии стандартных распределений

Пример 33. Распределение Бернулли В_р.

Пример 34, Биномиальное распределение В_n,_р. Воспользуемся свойством устойчивости биномиального распределения относительно
суммирования. Возьмем n «независимых случайных величин x₁..., x_n имеющих распределение Бернулли В_р = b₁,_p.

Тогда их сумма имеет распределение В_n,р. 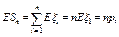так как все одинаково распределены и их математическое ожидание равно р; поскольку независимы и дисперсия каждой равна pq

Пример 35. Геометрическое распределение G_p

При р € (0, 1) (*)

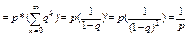
Равенство (*} появилось из-за нежелания дифференцировать сумму геометрической прогрессии, начинающейся не с 1, а c q. Заметьте, что производная у добавленных слагаемых равно 0, так что производные от этих двух сумм равны.

Поэтому

Пример 36. Распределение Пуассона

Доказать, что так что

Пример 37. Равномерное распределение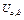

; ;

Пример 38. Стандартное нормальное распределение N_0,1

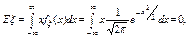поскольку под интегралом стоит нечетная функция, и сам интеграл абсолютно сходится
(за счет быстро убывающей ).

Последнее равенство следует из того, что а интеграл по всей прямой от плотности любого распределения равен 1, Поэтому

Пример 39, Нормальное распределение

Мы знаем, что если то , и Поэтому

Пример 40. Показательное (экспоненциальное} распределение

Найдем для произвольного 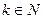момент порядка k.

В последнем равенстве мы воспользовались гамма-функцией Эйлера: Соответственно,

Date: 2016-08-30; view: 412; Нарушение авторских прав