Закон больших чисел Чебышева

Теорема. При числе испытаний, стремящихся к ¥ среднее арифметическое по вероятности сходится к математическому ожиданию.

Доказательство: Рассмотрим независимые, одинаково распределенные случайные величины X₁, X₂,..., X_n с конечным мат. ожиданием и дисперсией.

Рассмотрим их среднее арифметическое

Используя вспомогательное неравенство получим

получаем

Другая формулировка: Пусть x₁, x₂, …, x_n, … - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т.е. D(x_i)£C для любого i. Тогда, каково бы ни было x>0, справедливо соотношение

Смысл закона больших чисел Чебышева состоит в следующем. В то время как отдельная случайная величина может принимать значения, очень далёкие от своег математического ожидания, средняя арифмитическая большого числа случайных величин с вероятномтью, близкой к единице, принимает значение, мало отличающееся от среднего арифмитического их математического ожидания.

Теорема Чебышева

(Первое неравенство Чебышева) Если 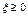, то ,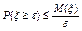

Доказательство. Замечая, что , и пользуясь основными свойствами математического ожидания получим

(Второе неравенство Чебышева)

Доказательство. Очевидно, что .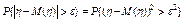

Применим первое неравенство Чебышева:

Date: 2016-08-30; view: 400; Нарушение авторских прав