Вопрос 29.1. Центральная предельная теорема для независимых одинаково распределенных случайных величин

Теорема. Пусть x₁, x₂, … — независимые и одинаково распределенные случайные величины с конечной и ненулевой

дисперсией: 0<Dx₁<¥. Обозначим через S_n сумму первых n случайных величин: S_n=x₁+…+x_n.

Тогда последовательность с. в. 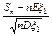слабо сходится к стандартному нормальному распределению.

Доказательство. Пусть x₁, x₂, … — последовательность независимых и одинаково распределенных случайных величин с конечной и ненулевой дисперсией. Обозначим через a математическое ожидание Ex₁ и через s² — дисперсию Dx₁. Требуется доказать, что

Введем стандартизованные случайные величины — независимые с.в. с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть Z_n есть их сумма . Требуется доказать, что

Характеристическая функция величины h равна

(26)

Характеристическую функцию с.в. z₁ можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты Ez₁=0, Ez₁²=Dz₁=1. Получим

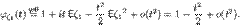
Подставим это разложение, взятое в точке , в равенство (26) и устремим к бесконечности. Еще раз воспользуемся замечательным пределом.

В пределе получили характеристическую функцию стандартного нормального закона. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости распределений стандартизованных сумм к стандартному нормальному распределению, что и утверждается в ЦПТ.

Date: 2016-08-30; view: 725; Нарушение авторских прав