
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вопрос 23.1. Определение кольца, примеры. Кольцо вычетов по модулю натурального числа, китайская теорема об остатках. Решение линейных сравнений.
|
|
Опр. Кольцом R с операциями “+” и “*” наз. мн-во, удовлетворяющее следующим условиям:
· (R,+) - абелева группа
· (R,*) - полугруппа
· выполняется закон дистрибутивности (a+b)c=ac+bc
Опр. Если операция “*” коммутативна, то кольцо наз. коммутативным.
Опр. Если в (R,*) есть е, то R – кольцо с единицей.
Опр. Пусть R – кольцо. Элемент а, принадлежащий R, наз. обратимым, если а обратим в (R,*). Обозначение: R*- мн-во всех обратимых элементов кольца R.
Опр. Мн-во R* наз. мультипликативной группой кольца.
Опр. Делителем нуля в кольце R наз. элемент а  R, а
R, а  0: существует b
0: существует b  R, b
R, b  0, a*b=0.
0, a*b=0.
Опр. Подкольцо I кольца R наз. идеалом, если для любогоi  I и любого r
I и любого r  R выполняется ir
R выполняется ir  I, ri
I, ri  I.
I.
Опр. Пусть R1…Rr – кольца. Пусть R – их декартово произведение, то есть это множество наборов R={(x1…xr): xi  Ri}. На множестве этих наборов длины r определяются есттественным образом операции “+”, “-“,”*”. То есть (x1…xr)+(y1…yr)=(x1+y1…xr+yr),
Ri}. На множестве этих наборов длины r определяются есттественным образом операции “+”, “-“,”*”. То есть (x1…xr)+(y1…yr)=(x1+y1…xr+yr),
(x1…xr)-(y1…yr)=(x1-y1…xr-yr), (x1…xr)*(y1…yr)=(x1*y1…xr*yr). Относительно определенных операций декартово произведение R так же является кольцом. Декартово произведение R, определенное подобным образом, наз. внешней (прямой) суммой колец R1…Rr.
Примеры колец:
· множество всех целых чисел;
· множество всех четных чисел и вообще целых чисел, кратных данному числу m;
· множество всех рациональных чисел;
· множество всех действительных чисел;
· множество всех комплексных чисел;
· множество всех многочленов от одного или нескольких переменных с рациональными, действительными или комплексными коэффициентами;
· множество всех функций, непрерывных на данном отрезке числовой прямой;
· множество всех квадратных матриц порядка n с действительными (или комплексными) элементами;
· множество всех векторов трехмерного пространства относительно обычного сложения и векторного умножения.
Опр. Кольцом вычетов по модулю m Zm наз. фактор кольцо кольца целых чисел по главному идеалу, порожденному элементом m.
Опр. Пусть nÎN, тогда j(n) – число взаимно простых с n чисел, не превосходящих n. j(n) наз. функцией Эйлера.
Теорема Эйлера. Пусть (a,m)=1Þ 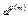
 1(mod m), где j - функция Эйлера.
1(mod m), где j - функция Эйлера.
Малая теорема Ферма. Пусть p - простое число. Тогда для всякого целого числа b, отличного от нуля, справедливо сравнение 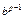
 1 (mod p).
1 (mod p).
Д-во:
Малая теорема Ферма является непосредственным следствием теоремы Эйлера, так как для простого числа p функция Эйлера j(p)=p-1.
Китайская теорема об остатках. Пусть m1, m2,..., mr -- попарно взаимно простые целые числа, a1, a2,..., ar -- произвольные целые числа. Тогда 1) найдется целое число x такое, что
x  a1 (mod m1),
a1 (mod m1),
x  a2 (mod m2), (1)
a2 (mod m2), (1)
...,
x  ar (mod mr).
ar (mod mr).
2) Решение системы (1) определено однозначно по модулю m1m2…mr.
Д-во:
Обозначим m1m2…mr через n, n/mj через nj.
В силу того, что m1, m2,..., mr - попарно взаимно простые целые числа, то (mj,nj)=1 (то есть чила nj и mj также взаимно просты). Тогда (по расширенному алгоритму Евклида) cуществуют tj и sj такие, что tjmj+sjnj=1.
Обозначим ej=sjnj. Тогда ej  1(mod mj), иными словами mjô(ej-1).
1(mod mj), иными словами mjô(ej-1).
В тоже время ei  1(mod mj), i
1(mod mj), i  j.
j.
Положим x=a1e1+…+arer.
Утверждается, что это число и есть решение системы (1). Проверим это.
Действительно x  ajej(mod mj)
ajej(mod mj)  aj(mod mj) для любого j от 1 до r. То есть x – решение системы (1).
aj(mod mj) для любого j от 1 до r. То есть x – решение системы (1).
Докажем однозначность. Пустьx1 – некоторое другое решение, то есть x1  aj(mod mj) для любого j от 1 до r. Отсюда следует, что x1-x
aj(mod mj) для любого j от 1 до r. Отсюда следует, что x1-x  0(mod mj) для любого j от 1 до r Þ любое mj÷(x1-x) Þ n=m1…mr÷(x1-x). А это как раз охначает, что x1
0(mod mj) для любого j от 1 до r Þ любое mj÷(x1-x) Þ n=m1…mr÷(x1-x). А это как раз охначает, что x1  x (mod n).
x (mod n).
Теорема (Критерий сравнимости).
a  b(mod m)Û m÷ (a-b)
b(mod m)Û m÷ (a-b)
Д-во:
Þ) a  b(mod m)Û a=m
b(mod m)Û a=m  +r, b=m
+r, b=m  +r Þ a-b=m
+r Þ a-b=m  +r-(m
+r-(m  +r)= m
+r)= m  -m
-m  =
=
=m( -
-  )
)
Ü)Пусть 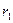 и
и  - остатки от деления.
- остатки от деления.
a-b=m( -
-  )+(
)+(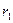 -
-  ). Это число делится на m Þ m÷ (
). Это число делится на m Þ m÷ (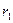 -
-  ).
).
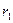 >0,
>0,  >0 и
>0 и 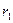 <m,
<m,  <m Þ
<m Þ 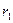 -
-  <m Þ m может делить
<m Þ m может делить 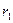 -
-  тогда и только тогда, когда
тогда и только тогда, когда 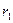 -
-  =0 Þ
=0 Þ 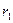 =
= 
Теорема. Если (a,m)=1, то сравнений ax  b(mod m)имеет единственное решение для любого b.
b(mod m)имеет единственное решение для любого b.
Date: 2016-08-30; view: 703; Нарушение авторских прав