
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вопрос 16.1. Определение кольца, примеры. Кольцо многочленов над полемб НОД и НОК многочленов, алгоритм Евклида. Кольцо многочленов над полем как кольцо главных идеалов.
|
|
Опр. Кольцом R с операциями “+” и “*” наз. мн-во, удовлетворяющее следующим условиям:
· (R,+) - абелева группа
· (R,*) - полугруппа
· выполняется закон дистрибутивности (a+b)c=ac+bc
Опр. Если операция “*” коммутативна, то кольцо наз. коммутативным.
Опр. Если в (R,*) есть е, то R – кольцо с единицей.
Опр. Пусть R – кольцо. Элемент а, принадлежащий R, наз. обратимым, если а обратим в (R,*). Обозначение: R*- мн-во всех обратимых элементов кольца R.
Опр. Мн-во R* наз. мультипликативной группой кольца.
Опр. Делителем нуля в кольце R наз. элемент а  R, а
R, а  0: существует b
0: существует b  R, b
R, b  0, a*b=0.
0, a*b=0.
Опр. Подкольцо I кольца R наз. идеалом, если для любогоi  I и любого r
I и любого r  R выполняется ir
R выполняется ir  I, ri
I, ri  I.
I.
Опр. Пусть R1…Rr – кольца. Пусть R – их декартово произведение, то есть это множество наборов R={(x1…xr): xi  Ri}. На множестве этих наборов длины r определяются есттественным образом операции “+”, “-“,”*”. То есть (x1…xr)+(y1…yr)=(x1+y1…xr+yr),
Ri}. На множестве этих наборов длины r определяются есттественным образом операции “+”, “-“,”*”. То есть (x1…xr)+(y1…yr)=(x1+y1…xr+yr),
(x1…xr)-(y1…yr)=(x1-y1…xr-yr), (x1…xr)*(y1…yr)=(x1*y1…xr*yr). Относительно определенных операций декартово произведение R так же является кольцом. Декартово произведение R, определенное подобным образом, наз. внешней (прямой) суммой колец R1…Rr.
Примеры колец:
· множество всех целых чисел;
· множество всех четных чисел и вообще целых чисел, кратных данному числу m;
· множество всех рациональных чисел;
· множество всех действительных чисел;
· множество всех комплексных чисел;
· множество всех многочленов от одного или нескольких переменных с рациональными, действительными или комплексными коэффициентами;
· множество всех функций, непрерывных на данном отрезке числовой прямой;
· множество всех квадратных матриц порядка n с действительными (или комплексными) элементами;
· 1множество всех симметричных матриц порядка n с действительными элементами относительно сложения матриц и йорданова умножения a о b = ╫(ab + ba), где в правой части стоят обычные произведения матриц;
· множество всех векторов трехмерного пространства относительно обычного сложения и векторного умножения.
Опр. Многочлен f(x)  P[x] наз. неприводимым над полем P (или неприводим в кольце P[x]), если deg f(x) >o и f(x) не имеет собственных делителей в кольце P[x].
P[x] наз. неприводимым над полем P (или неприводим в кольце P[x]), если deg f(x) >o и f(x) не имеет собственных делителей в кольце P[x].
Опр. Ненулевой многочлен со старшим коэффицентом, равным единице, наз. унитарным.
Опр. Любой многочлен f(x)  P[x] степени n>0 можно представить в виде f(x)=
P[x] степени n>0 можно представить в виде f(x)=  , где
, где 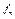 - старший коэффициент f(x),
- старший коэффициент f(x), 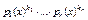 - унитарные, неприводимые, попарно различные (то есть попарно взаимно простые) многочлены из P[x] и
- унитарные, неприводимые, попарно различные (то есть попарно взаимно простые) многочлены из P[x] и 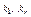
 N. Данное представление многочлена наз. каноническим разложением над полем P.
N. Данное представление многочлена наз. каноническим разложением над полем P.
Опр. Наибольшим общим делителем (НОД) многочленов 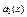 ...
... 
 P[x] наз. многочлен d(x)
P[x] наз. многочлен d(x)  P[x] такой, что:
P[x] такой, что:
1) d(x) есть общий делитель многочленов 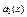 ...
... 
2) d(x) делиться на любой другой общий делитель этих многочленов
Опр. Наименьшим общим кратным (НОК) многочленов 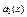 ...
... 
 P[x]наз. многочлен k(x)
P[x]наз. многочлен k(x)  P[x] такой, что:
P[x] такой, что:
1) k(x) есть общее кратное многочленов 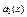 ...
... 
2) если  - любое общее кратное многочленов
- любое общее кратное многочленов 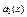 ...
...  , то k(x)ô
, то k(x)ô 
Алгоритм Евклида для нахождения НОД двух чисел.
Обозначим (a,b)= ( ,
,  ). Тогда
). Тогда
1.  =a=
=a=  b+
b+ 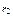
2. 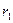 =b=
=b= 
 +
+ 
i. 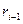 =
= 
 +
+ 
k-2. 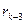 =
= 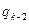
 +
+ 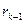
k-1.  =
= 
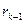 +
+ 
k. 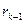 =
= 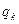
 +
+ 
Производится деление и наблюдается последовательность b> 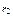 >...>
>...>  . Тогда на каком-то шаге последовательность должна оборваться. Пусть это произойдет на k-ом шаге и
. Тогда на каком-то шаге последовательность должна оборваться. Пусть это произойдет на k-ом шаге и  =0. Число d – последний неравный нулю остаток в алгоритме Евклида является НОД чисел a и b.
=0. Число d – последний неравный нулю остаток в алгоритме Евклида является НОД чисел a и b.
Date: 2016-08-30; view: 830; Нарушение авторских прав