Вопрос 8.1. Условные вероятности. Независимость событий. Формула полной вероятности. Формулы Байеса. Независимые случайные величины

ТЕОРИЯ ВЕРОЯТНОСТИ

Вопрос 1.1. Случайные величины, функции распределения, их свойства. Абсолютно непрерывные и дискретные распределения. Типовые распределения: биноминальное, пуассоновское, нормальное. Схема Бернулли и полиноминальная схема: основные формулы

Определение. Вероятностное пространство W - это набор элементов w_i, причём каждому вероятностному исходу w_i приписано определённое число p_i (p_i³0, åp_i=1), называемое вероятностью.

Определение. Событие - некоторый набор исходов.

Аксиома 1. Каждому случайному событию А соответствует определённое число Р(А), называемое его вероятностью и удовлетворяющее условию 0£Р(А)£1.

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3 (аксиома сложения вероятностей). Пусть А и В - несовместимые события. Тогда вероятность того, что произойдет хотя бы одно из них, равна сумме их вероятностей: Р(А+В)=Р(А)+Р(В).

Обобщение аксиомы 3. Если события А₁,…,А_N попарно несовместны, то P(A₁+…+A_N)=P(A₁)+…+P(A_N).

Классическое определение вероятности: Вероятностью Р(А) события отношение числа М исходов опыта, благоприятствующих событию А, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно независимых событий: Р(А)=М/N.

Определение. Рассмотрим функцию F(x), определенную на всей числовой оси следующим образом: для каждого x значение F(x) равно вероятности того, что дискретная случайная величина x примет значение, меньшее х, т.е. F(x)=P(x<x) (*). Эта функция называется функцией распределения вероятностей, или кратко, функцией распределения.

Вероятность попадания случайной величины в интервал x₁£x<x₂ равна приращению функции распределения на этом интервале. P(x₁£x<x₂)=F(x₂)-F(x₁) (**).

Основные свойства функции распределения:

1. Функция распределения является неубывающей. (Следует из (**) т.к. P³0)

2. Значения функции распределения удовлетворяют неравенствам 0£F(x)£1.(Из (*) F(-¥)=0, F(+¥)=1)

3. Вероятность того, что дискретная случайная величина x примет одно из возможных значений x_i, равна скачку функции распределения в точке x_i. ((**) х₁=x_i, x₂=x_i+Dx, P(x_i£x<x_i+Dx)=F(x_i+Dx)-F(x_i), Dx®0, lim P(x_i£x<x_i+Dx)=P(x=x_i)=p(x_i), lim F(x_i+Dx)=F(x_i+0), p(x_i)=F(x_i+0)-F(x_i).

Дискретные случайные величины. Рассмотрим случайную величину x, возможные значения которой образуют конечную или бесконечную последовательность чисел x₁, x₂, …, x_n,…. Пусть задана функция р(х), значение которой в каждой точке х=х_i (i=1, 2, …) равно вероятности того, что величина x примет значение х_i: p(x_i)=P(x=x_i). Такая случайная величина x называется дискретной. Функция р(х) называется законом распределения случайной величины, или законом распределения. p(x₁)+p(x₂)+…+p(x_n)+…=1. (Случайная величина - функция из вероятностного пространства x:W®R.)

Пример. Случайная величина x - число очков, выпадающих при однократном бросании игральной кости. Возможные значения x - числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что x примет любое из этих значений, одна и та же и равна 1/6.

Непрерывные случайные величины. Случайная величина x называется непрерывной, если для неё существует неотрицательная кусочно-непрерыная[1] функция j(х), удовлетворяющая для любых значений х равенству: . Функция j(t) называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если х₁<x₂, то

Схема Бернулли. Пусть, производится n независимых испытаний, в результате каждого из которых может наступать или не наступать событие А. Пусть вероятность наступления события А при каждом испытании равна р. Рассмотрим случайную величину x - число наступлений события А при n независимых испытаниях. Область изменения x состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей p(m) определяется формулой Бернулли: . Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как P_n(m) представляет собой m-й член разложения бинома (p+q)^m.

Пуассоновское распределение. Пусть случайная величина x может принимать любое целое неотрицательное значение, причём (k=0, 1, 2, …, n), где l - некоторая положительная постоянная. В этом случае говорят, что случайная величина x распределена по закону Пуассона. (при k=0 следует считать 0!=1). Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности p=l/n.

Пример. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равно 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных? Решение: Здесь l=np=1000*0,001=1, .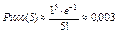

Нормальное распределение. Случайная величина x нормально распределена или подчиняется закону распределения Гаусса, если её плотность распределения j(x) имеет вид: , где а - любое действительное число, а s>0, функция распределения: .

Вопрос 8.1. Условные вероятности. Независимость событий. Формула полной вероятности. Формулы Байеса. Независимые случайные величины

Определение. Вероятность события А в предположении, что произошло событие В, называют условной вероятностью события А (P_B(A)).

Свойства условной вероятности:

1. P(W|B)=1

2. P(0|B)=0

3. 0£P(A|B) £1

4. AÌC => P(A|B) < P(C|B)

5. P(A+C|B)=P(A|B)+P(C|B)-P(AC|B) - формула сложения условных вероятностей.

6. P(AB)=P(B)P(A|B)=P(A)P(B|A) - формула умножения вероятностей

Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т.е. P(AB)=P(A)P_A(B) (*). В общем случае P(A₁A₂…A_n)=P(A₁)P_A1(A₂)P_A1A2(A₃)…P_A1A2…An-1(A_n).

Определение. Два события А и В называются независимыми, если предположение о том, что произошло одно из них, не изменяет вероятность другого, т.е. если P_B(A)=P(A) и P_A(B)=P(B).

Из (*) таким образом следует, что если два события независимы, то P(AB)=P(A)P(B).

События А₁, А₂, …, A_n называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько их остальных событий осуществились.

Формула полной вероятности. Пусть событие А может произойти только вместе с одним из попарно несовместных событий H₁, H₂, …,H_n, образующих полную группу. Тогда, если произошло событие А, то это значит, что произошло одно из попарно несовместных событий H₁A, H₂A, …,H_nA. Следовательно, А= H₁A+H₂A+…+H_nA. Т.к. P(H_iA)=P(H_i)P_Hi(A), то P(A)=P(H₁)P_H1(A)+ P(H₂)P_H2(A)+…+ P(H_n)P_Hn(A). Эта формула называется формулой полной вероятности. События H₁, H₂, …,H_n часто называют гипотезами.

Формула Байеса. Предположим, что производится некоторый опыт, причём об условиях его проведения можно высказать n единственно возможных и несовместных гипотез H₁, H₂, …,H_n, имеющих вероятности P(H_i). Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы H_i, то P_Hi(A)=p_i (i=1, …,n). Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, чему равно P_A(H_i).

Эта формула называется формулой Байеса.

Случайные величины X и Y независимы, если P(X<x,Y<y)=P(X<x)P(Y<y), т.е. F(x,y)={функция совместного распределения}=F_X(x)F_Y(y), где F_X(x) и F_Y(y) - функции распределения (см. Вопрос 2) X и Y.

Date: 2016-08-30; view: 597; Нарушение авторских прав