Свойства математического ожидания

Е0. Математическое ожидание случайной величины есть ЧИСЛО!

Е1.Для произвольной функции g: R —> R

· = , если распределение дискретно;

· = , если распределение абсолютно непрерывно.

Доказательство. Мы докажем это свойство (как и. почти все дальнейшие) только для дискретного распределения. Пусть принимает значения c₁,c₂,… c вероятностями 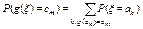. Тогда

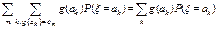
E2. Математическое ожидание постоянной равно этой постоянной: .

ЕЗ. Постоянную можно Вынести за знак математического ожидания

Доказательство: Следует из свойства Е1 при g(x)=cx.

Е4. Математическое ожидание суммы любых случайных величин и равно сумме их математических ожиданий: .

Доказательство. Для величин с дискретным распределением: пусть x_k и у_п — значения соответственно, Для функции можно доказать свойство, аналогичное Е1.Пользуясь этим свойством для g (х,у) = x + у, запишем:

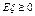E5. Если п.н. («почти наверное», то есть с вероятностью 1; ), то . Если п.н., и при этом , то п.н., то есть .

Следствие 12. Если п.н., то . Если п.н., и при этом , то п.н.

Е6. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: если и независимы, то .

Доказательство.

Date: 2016-08-30; view: 328; Нарушение авторских прав