
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерии оценки статистических гипотез
|
|
Постановка задачи
Понятие статистической гипотезы предполагает проведение статистической оценки для объективного подтверждения или отклонения рассматриваемого предположения. Статистические гипотезы подразделяют на виды:
· параметрические (требуется вычисление параметров распределения - среднего, дисперсии и т.д.);
· непараметрические (не требуется вычисление параметров распределений).
Пример 4.1. Параметрическими гипотезами являются утверждения: средние значения диаметров деревьев в двух выборках равны между собой, дисперсии значений высот деревьев в двух выборках не равны между собой и т.д. Непараметрическими гипотезами являются утверждения: распределение деревьев по диаметру в древостое подчиняется закону нормального распределения, рост древостоя по высоте описывается экспоненциальной кривой и т.д.
На основании статистической оценки решается вопрос: принять или опровергнуть гипотезу. Для решения этого вопроса необходимо выполнить следующее:
· рассмотреть не только проверяемую гипотезу, но и исключающую ее альтернативную гипотезу;
· выбрать статистический критерий - показатель, разделяющий доверительные зоны, каждая из которых свидетельствует о наличии проверяемой или альтернативной гипотезы.
Более подробно остановимся на критериях, позволяющих ответить на следующие наиболее часто возникающие в лесохозяйственной практике вопросы:
1) относится ли та или иная варианта к данной статистической совокупности?
2) соответствует ли данное эмпирическое распределение тому или иному теоретическому распределению?
3) являются ли данные эмпирические совокупности выборками из одной и той же генеральной совокупности?
Первый вопрос в общем ставится так. Имеется некоторая выборочная статистическая совокупность. Некоторые варианты очень далеко отстоят от среднего значения, и возникает сомнение, является ли это результатом маловероятных, но все же возможных больших отклонений от центра соответствующей генеральной совокупности, или же результатом того, что в рассматриваемую выборку почему-то оказались включенными варианты, принадлежащие в действительности к другой генеральной совокупности.
Второй вопрос возникает в связи с тем, что из-за случайности в образовании выборки распределение вариант в выборке всегда отличается от их распределения в генеральной совокупности; поэтому если в генеральной совокупности варианты распределены по определенному теоретическому закону, то распределение в выборке будет заведомо отклоняться от этого закона. (Отсюда следует, что сам факт отклонения выборочного распределения от того или иного теоретического распределения еще не дает основания утверждать, что и в генеральной совокупности распределение не подчиняется данному теоретическому закону.) Таким образом, вопрос сводится к тому, можно ли расхождение между выборочным и предположенным теоретическим распределениями отнести за счет расхождения между выборкой и генеральной совокупностью или же оно является результатом того, что сама генеральная совокупность отклоняется от данного теоретического распределения.
Сущность третьего вопроса совершенно аналогична: расхождение между эмпирическими распределениями может быть просто расхождением между разными выборками из одной и той генеральной совокупности, но может также объясняться тем, что они выбраны из разных генеральных совокупностей.
Во всех трех случаях приходится ответить на вопрос о том, является ли наблюдаемое различие между объектами отражением какого-то реального различия или же оно есть результат случайности, сопровождающей попадание вариант в выборку. Это позволяет сформулировать общий подход к решению всех этих задач. В любом случае задача может быть сведена к проверке гипотезы об отсутствии реального различия. Эту гипотезу называют нулевой гипотезой; обычно для нее применяется специальное обозначение Нo. Ее сущность сводится к предположению, что разница между генеральными параметрами сравниваемых групп равна нулю и что различия, наблюдаемые между выборочными характеристиками, носят не систематический, а исключительно случайный характер. Так, если одна выборка извлечена из нормально распределенной совокупности с параметрами mx и sx, а другая из совокупности с параметрами my и sy, то нулевая гипотеза исходит из того, что mx = my и sx = sy. Противоположная нулевой - альтернативная гипотеза Нa - исходит из предположения, что mx ¹ my и sx ¹ sy.
В первой задаче нулевая гипотеза гласит о том, что сомнительная варианта принадлежит к той же генеральной совокупности, что и данная эмпирическая совокупность. Во второй задаче проверке подлежит нулевая гипотеза о том, что различие между выборочным распределением и теоретическим является случайным, то есть, что нет реального различия между распределением в генеральной совокупности, из которой взята выборка, и предположенным теоретическим распределением. В третьей задаче нулевая гипотеза состоит в том, что данные эмпирические совокупности являются выборками из одной и той же генеральной совокупности, так что между генеральными совокупностями, выборками из которых являются данные эмпирические совокупности, нет реального различия.
Правильность нулевой гипотезы можно проверить следующим образом. Предположив справедливость нулевой гипотезы, т. е. отсутствие реального различия, мы вычисляем вероятность того, что из-за случайности выборки расхождение может достигнуть фактически наблюденной величины; если эта вероятность окажется очень малой, то нулевая гипотеза отвергается (т. е. маловероятно, что расхождение вызвано случайными причинами, а не реальным различием).
Предельно допустимое значение вероятности, начиная с которого вероятность можно считать малой, называют уровнем значимости. Различие считается значимым (т. е. реальным), если вероятность того, что нулевая гипотеза верна, меньше уровня значимости (его обозначают буквой a).
Очевидно, уровень значимости характеризует, в какой мере мы рискуем ошибиться, отвергая нулевую гипотезу. Этот выбор в значительной мере определяется конкретными задачами исследования. Например, если исследуется новый лечебный препарат и нужно показать, что его побочное действие не опасно для жизни, то даже уровень значимости 0,1% должен считаться не слишком высоким. Наоборот, если речь идет об улучшении продуктивности древостоя за счет недорогого внесения удобрений, то достаточно и небольшой уверенности о положительном результате. При этом, разумеется, не исключаются дальнейшие уточнения экспериментальных данных (например, путем постановки дополнительных опытов, последующих наблюдений и т. д.). В лесохозяйственных исследованиях часто считают достаточным 5%-й уровень значимости (вероятность ошибочной оценки P =0,05). При этом нулевую гипотезу не отвергают, если P >0,05. Если же P <0,05, то нулевую гипотезу следует отвергнуть на принятом уровне значимости a.
В общем виде использование статистических критериев (К) в области лесного дела при строгом доказательстве нулевой гипотезы можно представить схематически:
K05 > Kф > K01

 Не отвергается Отвергается
Не отвергается Отвергается
 |  |
Н у л е в а я г и п о т е з а
где
Kф – значение фактически полученного критерия;
K05, K01 - значения критериев на 5% -ном и 1% -ном уровнях зна - чимости.
Необходимо всегда иметь в виду, что утверждение о том, что нет достаточных оснований отвергать гипотезу об отсутствии различия, вовсе не равносильно утверждению, что отсутствие различия доказано. Иными словами, можно лишь утверждать, что данные наблюдений не противоречат предположению об отсутствии различия, но нельзя утверждать, что эти данные доказывают отсутствие такого различия. Ошибка, которая допускается, когда не отвергают гипотезу Hо, в действительности неверную, носит название ошибки II рода, в отличие от рассмотренной выше ошибки I рода, когда отвергают гипотезу Hо, на самом деле верную. Вероятность ошибки II рода обозначается β.
В лесном хозяйстве применяют два вида статистических критериев:
· параметрические, построенные на основании параметров данной выборки (например, M, s и т.д.);
· непараметрически е, представляющие собой функции, зависящие непосредственно от вариант данной выборки с их частотами.
При нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические критерии. Они способны безошибочно отвергать нулевую гипотезу, если она не верна. В случае очень больших отличий распределений признака от нормального вида следует применять непараметрические критерии, которые в этой ситуации оказываются часто более мощными. В случаях, когда варьирующие признаки выражаются условными знаками, применение непараметрических критериев оказывается единственно возможным.
4.2. Проверка гипотезы о принадлежности варианты к совокупности
При статистической обработке биологического материала часто сталкиваются с наличием в исследуемой совокупности некоторого количества вариант, значения которых довольно резко отличаются от основной массы наблюдений. Появление таких вариант может объясняться естественной вариабильностью случайной величины, вследствие которой большие отклонения от центра распределения не исключены. Они могут также свидетельствовать о неоднородности статистической совокупности. Если вариантами являются значения какого-либо показателя для разных особей некоторой популяции, то неоднородность будет следствием попадания в совокупность особей из другой биологической популяции; если вариантами являются результаты каких-то повторных замеров на одном и том же объекте, то неоднородность будет следствием спорадических нарушений стандартных условий эксперимента.
Конечно, появление резко выделяющихся вариант указывает прежде всего на необходимость тщательной проверки исследуемой популяции или обстановки эксперимента. При этом варианты, условия получения которых противоречили стандарту, должны отбрасываться независимо от их значений. Однако во многих случаях не удается получить прямых указаний о неоднородности изучаемой совокупности. Тогда приходится прибегать к статистическим критериям.
Применение последних основано на том, что если распределение вариант в генеральной совокупности нормально или близко к нормальному, то появление в выборке вариант, далеко отклоняющихся от центра распределения, хотя и возможно, но очень маловероятно.
Очевидно, при построении критерия исключения (соответствующее критическое значение обозначим τa) надо исходить из условия, что в выборке данного объема n из нормальной генеральной совокупности не должно содержаться, с определенной вероятностью Р, ни одной варианты, отклоняющейся от x больше, чем на τas. Выбранный уровень значимости
a = 1 - Р имеет здесь тот смысл, что если выбрать из нормальной генеральной совокупности большое число выборок объема n каждая, то в среднем лишь в 100 a процентах из них будут попадаться варианты вне пределов х ± as, а 100 (1 — a) = 100 Р процентов выборок не будут содержать вариант вне этих пределов. Из сказанного ясно, что критические значения τa должны зависеть как от принятого уровня значимости a, так и от объема выборки n.
Табл. 4.1 содержит некоторые критические значения τa(n). При построении критерия принято во внимание то, что значения μ и σ обычно неизвестны и заменяются их оценками M и s, так что
τmax = (xmax - M)/s; τmin = (M-xmin)/s. (4.1)
Таблица 4.1
| τα | 5% | 1,92 | 2,41 | 2,78 | 2,96 | 3,08 | 3,16 | 3,22 | 3,40 | 3,61 |
| 1% | 1,97 | 2,62 | 3,08 | 3,29 | 3,42 | 3,52 | 3,58 | 3,77 | 3,98 | |
| n | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 100 | 200 |
Пример 4.2. На рис 4.1 в среде пакета MS Excel дано распределение по весу семян определенной древесной породы, взятых из семенного фонда. Обращает на себя внимание присутствие в этой совокупности трех семян с весом 22 мг, очень сильно отклоняющимся от среднего для данного сорта веса 31,74 мг. Объяснение может быть двояким. С одной стороны, это может быть следствием естественной вариабильности веса семян древесной породы - ведь при нормальном распределении отклонения могут быть довольно большие. С другой стороны, появление в выборке х трех семян с весом 22 мг может являться следствием того, что в рассматриваемый семенной фонд по какой-то причине попало некоторое количество семян, не соответствующих кондиционным нормам.
Так как в данном случае отклонение сомнительных вариант от среднего значения составляет 31,74 - 22,0 = 9,74, а s = 3,343, то
τmin = (M - xmin)/ s = 9,74/3,343 = 2,914.
В табл. 4.1 находим, что критическое значение τ05(100) составляет 3,40. Поскольку τmin < τ05, нулевая гипотеза о принадлежности рассматриваемых трех вариант к данной совокупности не может быть отвергнута. Если нулевая гипотеза отвергается, то это значит, что сомнительные варианты квалифицируются как «артефакты». В таком случае их следует выбрасывать из дальнейшей обработки.
При большом объеме выборки вопрос об исключении «артефактов» не стоит особенно остро, так как относительный «вес» нескольких сомнительных вариант при вычислении усредненных параметров сравнительно невелик. Если же выборка мала, то даже одно неправильное значение может заметно исказить результат усреднения.
 |
Рис. 4.1
4.3. Сравнение эмпирического распределения с теоретическим (критерий "хи-квадрат")
При решении вопроса о различии между эмпирическим распределением и теоретическим нулевая гипотеза заключается в том, что генеральная совокупность, выборкой из которой является данное эмпирическое распределение, распределена по предполагаемому теоретическому закону, а отклонение эмпирического распределения от теоретического есть просто отклонение выборочного распределения от генерального (из-за случайного характера образования выборки).
Проверку гипотез о законах распределения производят с помощью специально разработанных критериев. Один из них - критерий согласия c2 (предложен К.Пирсоном в 1890 г.) - нашел широкое применение в лесном хозяйстве. Критерий представляет собой сумму квадратов отклонений эмпирических частот n от теоретических n', отнесенную к теоретическим частотам:
 . (4.2)
. (4.2)
Распределение вероятных значений случайной величины c2 является непрерывным и асимметричным. Оно зависит от числа степеней свободы k и приближается к нормальной кривой по мере увеличения числа испытаний N. Для того, чтобы оценки были более точными, выборка должна содержать не менее 50 вариант. Поэтому часто считают, что применение критерия c2 требует того, чтобы в крайних классах вариационного ряда содержалось не менее пяти вариант. Если в крайних классах содержится меньше, чем пять вариант, то вычисленные и эмпирические частоты объединяются до указанного минимума и соответственно уменьшают число классов вариационного ряда. Число степеней свободы устанавливают по вторичному числу классов с учетом ограничений свободы вариации, которая бывает разной. Так, при оценке эмпирических распределений, следующих нормальному закону, число степеней свободы k=N-3 (с учетом трех ограничений вариации этого закона).
Для проверки нулевой гипотезы нужно фактически полученную величину cф2 сравнить с ее критическим значением cst2. Если cф2³cst2, то нулевая гипотеза должна быть отвергнута на принятом уровне значимости a с числом степеней свободы k. Значения теоретических критериев cst2 приведены в Приложении 3.
Пример 4.3. Проверим гипотезу о согласии между теоретическим (логнормальная модель) и эмпирическими рядами распределения диаметра из табл. на рис. 4.2. Вычисленное в MS Excel значение cф2 = 2,78. Число степеней свободы k= 8-3=5. Табличное значение критерия при k =5 при a=0,1 равно c012 = 15,09. Следовательно, вычисленная статистическая характеристика попадает в зону допустимых значений, и гипотеза о соответствии ряда распределения логнормальному закону не отвергается.
4.4. Сравнение средних значений двух эмпирических совокупностей (критерий Стьюдента)
Английский математик В. Госсет в 1908 г. нашел закон распределения величины
 ,
,
 |
Рис. 4.2.
в которой генеральный параметр s заменен на его выборочную характеристику s, т.е. нашел закон распределения значений
 . (4.3)
. (4.3)
Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:
 для -¥ < t< +¥, (4.4)
для -¥ < t< +¥, (4.4)
где
С - константа, зависящая только от числа степеней свободы;
k = n -1.
Из приведенной зависимости следует то, что t -распределение зависит только от объема выборки n, причем с увеличением n t -распределение быстро приближается к нормальному с параметрами m=0 и s=1 и уже при n ³30 не отличается от него.
Для практического использования t -распределения составлена специальная таблица, в которой содержатся критические значения t st для разных уровней значимости a и чисел степеней свободы k (Приложение 1). Сравнивая друг с другом две независимые выборки, взятые из нормально распределенных совокупностей с параметрами m1 и m2, обозначим m1 - m2 = D, а дисперсию этой разницы s2D. Значения генеральных параметров неизвестны, однако можно найти величины выборочных средних M1, M2, разность между ними M1 - M2 = d и ошибку разницы sd. Ошибка разности средних sd определяется по следующим формулам:
 (4.5)
(4.5)
или
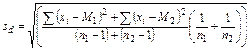 .
.
Так как, согласно H0 - гипотезе m1 - m2 = 0, то t -критерий выражается в виде отношения разности выборочных средних к своей ошибке, т.е.
t = d / s d . (4.6)
H0 - гипотезу отвергают, если фактически установленная величина t -критерия t ф превысит или окажется равной критическому значению t st для принятого уровня значимости a и числа степеней свободы k = n1 + n2 -2, т.е. t ф³ t st .
Вышеизложенное применение t -критерия предполагает, что дисперсии сравниваемых групп одинаковы. Если это не так, то величину критерия и число степеней свободы находят по формулам:
 , (4.7)
, (4.7)
 . (4.8)
. (4.8)
Пример 4.4. Необходимо выяснить эффективность воздействия двухприемных постепенных рубок главного пользования на естественное лесовозобновление в сухих лишайниковых сосняках. Опыт может быть поставлен следующим образом: в качестве контроля закладывается делянка, на которой проводится сплошная рубка деревьев, в качестве опытного варианта служит двухприемная постепенная рубка. Площадки по учету возобновления одного размера размещаются в систематическом порядке вдоль делянок. При подсчете возобновления сосны получились результаты, приведенные на рис. 4.4, из которых следует, что средние значения для опытной и контрольной делянок не совпадают. Однако это еще не дает основания считать доказанной эффективность применения постепенных рубок в лишайниковых сосняках.
На рис. 4.3. приведена последовательность нахождения значений t -критерия t ф = 2,01 и числа степеней свободы k=26 рассматриваемой задачи с использованием программы MS Excel. Так как t ф< t 01 (26)» 2,7 (см. Приложение 1), то нулевая гипотеза не отвергается. Следовательно, расхождение между опытом и контролем можно считать незначимым, т.е. применение постепенных рубок в сухих лишайниковых сосняках не обеспечивает увеличения естественного возобновления леса.

Рис. 4.3.
Пример 4.5. Каждый из двух сортов условной растениеводческой продукции высевался на семи делянках одного размера. На рис. 4.4 приведена урожайность в кг. Урожай сорта II на одной из делянок был поврежден и поэтому не включен в дальнейшую обработку. Там же приведена последовательность нахождения значений t -критерия рассматриваемой задачи с использованием программы MS Excel.
Так как средний урожай сорта I (M1 = 8,27) выше, чем для сорта II (M2 = 6,78), то напрашивается вывод, что вообще сорт I более урожайный. Но такой вывод может оказаться ложным, т.к. каждое из чисел 8,27 и 6,78 есть не генеральное, а выборочное среднее. Другая случайная выборка, также состоящая из 7 делянок, наверняка дала бы для M1 значение, отличное от 8,27; в частности, это новое значение могло бы оказаться меньше, чем 8,27. С другой стороны, и для M2 выборка дала бы значение, отличное от 6,78, в частности, могло бы получиться число большее, чем 6,78. Поэтому повторение всего опыта с обоими сортами могло бы дать результат M1 < M2. Очевидно, вероятность такого исхода тем меньше, чем больше отношение M1 - M2 к sd.
Таким образом, опять приходим к критерию Стьюдента для оценки значимости того, что M1 превышает M2. Значение t -критерия t ф = 3,15, а число степеней свободы k =11. Так как t ф> t 01 (11)» 2,17 (см. Приложение 1), то нулевая гипотеза отвергается.

Рис. 4.4.
Date: 2016-07-25; view: 909; Нарушение авторских прав