Семейство кривых распределения Джонсона

Это семейство включает три типа кривых, представляющих распределение неограниченных случайной величины (тип SU), ограниченных с одной стороны (SL) и ограниченных с двух сторон (SB). В общем виде семейство кривых Джонсона требует знания параметра положения x, параметра масштаба l и двух параметров формы - g и d.

Для выбора конкретной кривой необходимо установить, к какому типу принадлежит эмпирическое распределение. Для этой цели на основании ряда распределения вычисляют выборочные значения b₁ и b₂ и по графику (рис. 3.8) устанавливают тип распределения. Выборочные распределения, для которых b₁ и b₂ лежат вблизи и на линии SL, относятся к этому типу; лежащие ниже линии SL - к типу SU, а выше, исключая критическую область, - типу SB. Затем по выборке оценивают параметры данного типа распределения и вычисляют выравнивающие частоты.

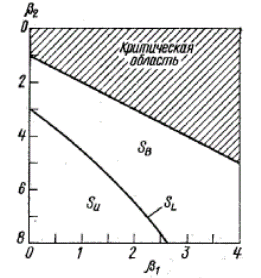Рис. 3.8.

Тип SL. Кривая распределения ограничена слева точкой x, а значения x ³x. Этот тип распределения зависит только от трех параметров d, x и g*=g-dlnl. Плотность распределения для нормированных значений величины x путем замены y =(x -x)/l имеет следующий вид (y ³0):

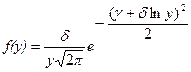. (3.18)

Положив d=1/s и g*= M /s, получаем трехпараметрическое логнормальное уравнение, поэтому аппроксимация этого распределения возможна методом, рассмотренным в п. 3.3.

В практике использования типа SZ может встретиться два случая:

· величина x известна;

· величина x неизвестна.

В большинстве задач по аппроксимации величин в лесном деле, особенно для свертки информации, начало кривой распределения, т. е. величина x, как правило, может быть установлена (например, в качестве x можно использовать нижнюю границу первого класса ряда распределения). Если значение x известно, то, вычислив значения

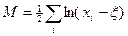, (3.19)

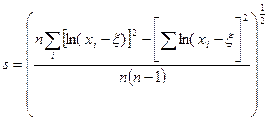, (3.20)

находят два неизвестных параметра d=1/s и g*= M/s формулы (3.18).

Если значение x неизвестно, то из формулы преобразования исходного распределения с плотностью f (x) к нормированной нормально распределенной величине z имеем:

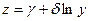(3.21)

заменой g*=g-dln(x-x) находят

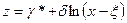. (3.22)

Так как по выборке необходимо оценить параметры g*, d и x, составляют три уравнения, приравнивающих три выборочных квантиля трем соответствующим квантилям нормированной нормально распределенной величины z

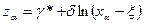, (3.23)

где

z _a и x _a - соответственно теоретические и выборочные квантили.

Целесообразно выбирать два симметричных квантиля, что упрощает расчеты, в противном случае приходится решать нелинейное уравнение. Вполне приемлемо брать a=0,05; 0,5 и 0,95 (выбор других близких квантилей мало меняет результаты). Так как для нормированного нормального распределения z _0,05=1,645, z _0,5=0 и z _0,95=1,645, решением системы трех уравнений (3.24) находят:

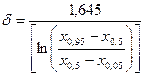, (3.24)

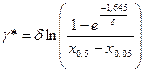, (3.25)

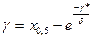. (3.26)

Поскольку техника вычисления выравнивающих частот по уравнению типа SL по сути одинакова для обоих описанных выше случаев, рассмотрим ее на примере аппроксимации при неизвестном x,.

Пример 3.7. Вычислим выравнивающие частоты для ряда распределения диаметра из рис 3.9. Имеем b₁= 1,0300 и b₂=4,3262, т. е. распределение принадлежит к типу SL семейства кривых Джонсона. Для определения параметров d, g* и x выберем квантили, соответствующие вероятностям 0,05; 0,5; 0,95. Они соответственно равны 10,57; 17,31 и 29,74. По (3.24) - (3.26) получаем: d=2,688, g*=-7,229 и x=2,588.

Теоретические частоты по вычисленным выборочным оценкам определяют по формуле (3.22) с использованием в качестве квантилей границ классов эмпирического распределения. По условию z= g*+ d×ln(x_p-x) - нормированная нормально распределенная случайная величина. По таблицам F (z) или непосредственно в пакете прикладных программ (в MS Excel с помощью функции НОРМСТРАСП ()) находим накопленную вероятность, соответствующую верхним границам классов ряда распределения, откуда умножением на общее количество наблюдений n =558 переходят к выравнивающим (накопленным) частотам. Вычисления в среде пакета MS Excel приведены на рис. 3.9, откуда следует, что расхождения между теоретическими и эмпирическими частотами относительно невелики.

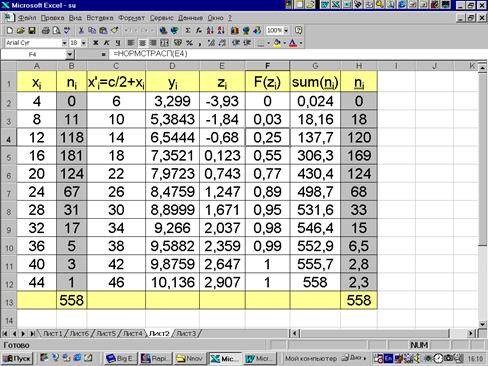
Рис. 3.9.

Тип SB. Преобразование и плотность кривых распределения типа SB имеют следующий вид:

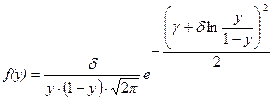. (3.27)

представляет случайные величины, ограниченные с двух сторон значениями x= x ₁ и х ₂=x+l, где параметр x - начало кривой, а l - размах распределения, или расстояние между крайними значениями. Кривая типа SB может принимать различную форму (рис. 3.10).

При аппроксимации кривыми типа SB возможны три случая:

· известны оба крайних значения;

· одно из них;

· ни одного.

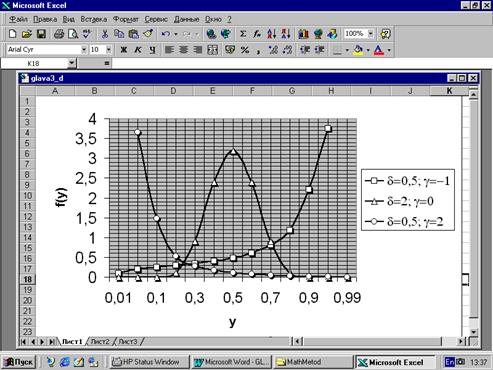
Рис. 3.10.

Если оба крайних значения известны, то остается оценить g и d. Как и для типа SL, оценки находят приравниванием теоретических и выборочных квантилей.

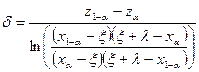; (3.28)

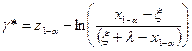. (3.29)

Если известно одно крайнее значение x, то для оценки трех параметров составляют систему из трех уравнений, в третьем из которых обычно в качестве соответствующих квантилей используют медиану. Тогда оценки d, g и l находят решением системы (3.28)-(3.29) с добавлением третьего уравнения для определения

.

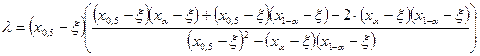(3.30)

Техника аппроксимации типом SB такая же, как и типом SL:

1) находят выборочные значения квантилей для некоторых выбранных заранее вероятностей (один квантиль - медиана, два других - симметричные);

2) по формулам (3.28)-(3.30) находят выборочные значения d, g* и l (или по формулам (3.28)-(3.30), если x известно);

3) по схеме, аналогичной примеру 3.7, вычисляют квантили z _p, соответствующие квантилям x _р - границам классов аппроксимируемого ряда распределения;

4) по таблице нормированного нормального распределения (или непосредственно в пакете прикладных программ) вычисляют значения накопленных вероятностей, от которых переходят к теоретическим частотам.

Пример 3.8. В первых двух колонках табл. на рис. 3.11 приведен ряд распределения высоты (в сантиметрах) жизнеспособного 3-летнего самосева ели. В качестве жизнеспособного учтен самосев высотой от 0,5 см. Аппроксимируем этот ряд при помощи кривых семейства кривых Джонсона.

Определим для ряда моменты (см. рис. 3.9). Если в качестве начального значения взять x _о=4, то начальные моменты m ₁=-0,7442, m ₂=6,2053, m ₃=-0,8768, m ₄=69,3000; центральные m ₂=5,6515, m ₃=12,1529, m ₄=86,3899; основные r ₃=0,9045, r ₄=2,7048. Отсюда b ₁=0,8181, b ₂=2,7048, т. е. по графику рис. 3.8 имеем тип SB. Примем, что начало кривой x =0,5. Для вычисления d, g* и l используем квантили a =0,05; 0,5 и 0,95. По (2.10) или с использованием функции МЕДИАНА() MS Excel имеем: x _0,05=0,65; x _0,5=2,48; x _0,95=8,21. Подставив значения квантилей x _0,05 и x _0,95=8,21 и использовав табличные значения z _0,05 и z _0,95, находим: l= 9,5; d =0,59; g* =0,78.

Дальнейшие вычисления идут по схеме аналогично примеру 3.7. Значение z= g*+ d×ln(x_p-x/l+x - x_p). В целом аппроксимацию можно считать приемлемой.

Если неизвестны все крайние значения, то по числу неизвестных параметров составляют четыре уравнения, в которых четыре выборочных квантиля приравнивают к соответствующим квантилям нормированного нормального распределения. Оценки параметров d, g*, l и x определяют из системы нелинейных уравнений. Случаи с четырьмя неизвестными параметрами в лесном деле крайне редки, а в задачах свертки информации практически исключаются. Поэтому более детально тип SB здесь не рассматривается.

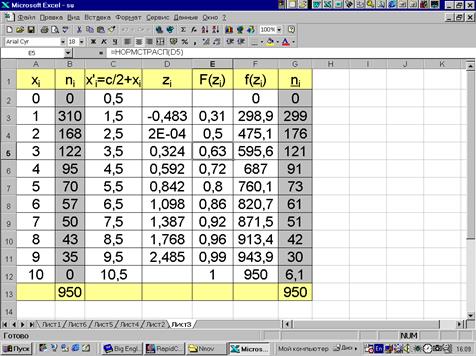
Рис. 3.11.

Тип SU. Плотность кривых распределения типа SU (рис. 3.12) имеют следующий вид (¥< y <¥):

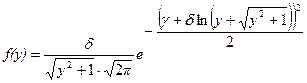. (3.31)

В задачах аппроксимации кривыми этого типа требуется оценка всех четырех параметров. Как и в аналогичном случае типа SB, составляют систему уравнений, в которых приравнивают четыре выборочных и четыре теоретических квантиля. Это приводит к нелинейной относительно искомых параметров системе, поэтому Н. Джонсон предложил таблицы для нахождения по значениям b ₁ и b ₂ оценок параметров d и g*. Величины l и x вычисляют по формулам:

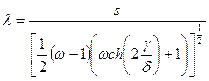; (3.32)

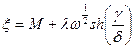, (3.33)

где

;

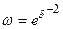ch x = (e^x+e^-x)/2; ch(- x)=сh(x);

sh x = (e^x - e^-x)/2; sh(-х) =-sh(x).

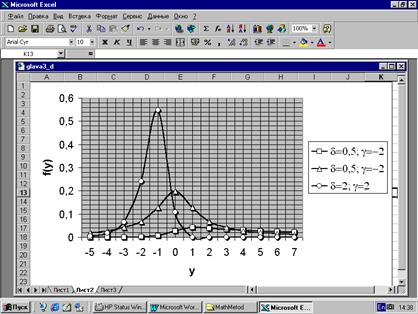
Рис. 3.12.

Техника вычислений иллюстрируется следующим примером:

Пример 3.9. На рис. 3.13 приведен ряд распределения, составленный но результатам 250 случайных замеров диаметра стволов деревьев на высоте груди. Статистики ряда следующие: M =29,43 см; s =0,4454 см; b ₁=0,0527; b ₂=4,96. По таблицам Джонсона (Приложение 5) находим g =-0,1972; d =1,86. По (3.32) и (3.33) вычисляем l=0,706 и x=29,34. Значения y=(x’-x)/l, а z=g+d*arcsh(y). Значение гиперболического косинуса вычисляется в MS Excel с помощью функции ASINH (), а стандартного нормального интегрального распределения F(z) - НОРМСТРАСП ().Как видно из сравнения частот n и n, в целом кривая типа SU хорошо аппроксимирует эмпирический ряд.

Date: 2016-07-25; view: 1704; Нарушение авторских прав