Логнормальное распределение

Формируется в условиях, аналогичных предыдущему. Величина x распределена логнормально, если логарифмы ее значений u = ln x имеют нормальное распределение:

, (3.5)

где

u - среднее ln x;

s_u - дисперсия ln x.

Распределение зависит от двух параметров (среднего и дисперсии логарифмов значений x), хотя можно ввести один или два параметра, ограничивающие размах распределения с одной или двух сторон.

Кривая распределения имеет правостороннюю асимметрию (рис. 3.2), которая возрастает с увеличением s_u, поэтому хорошо аппроксимирует распределения с положительной косостью. Если для величины x известно среднее M и дисперсия s², то параметры логнормального распределения можно вычислить непосредственно по формулам:

s_u² = ln(s²/ M ² +1), (3.6)

M _u = ln M - s_u²/2, (3.7)

а плотность логнормального распределения величины x

. (3.8)

Уравнение (3.8) задано на интервале [0, ¥].

Имеются многочисленные примеры использования логнормального распределения как модели при свертке лесоводственной информации.

Пример 3.3. Вычислим выравнивающие частоты для ряда распределения диаметра табл. 2.1. Среднее значение и дисперсия этого ряда соответственно равны M =18,36 (см), s²=34,215 (см²), а s=5,85 (см). По (3.6) и (3.7) находим о_u=0,311, M_u=2,862. Сравнение эмпирических и вычисленных частот свидетельствует о хорошем соответствии принятой модели ряду распределений (рис. 3.3).

Рис. 3.2.

Рис. 3.3.

3.4. Гамма - и бета- распределения

Принадлежат к числу основных моделей, используемых при изучении распределений. Оба они связаны с одним из наиболее общих распределений - раcпределением Маркова, из которого можно получить практически все встречаемые в приложениях распределения как предельные стохастические кривые. Условия, при которых формируются гамма- и бета-распределения, весьма широки, в зависимости от величины входящих в них параметров. Как правило, они могут описывать любую практическую ситуацию из приведенных в настоящем параграфе, а ряд рассмотренных распределений может быть получен как частные случаи гамма- и бета- распределений.

3.4.1. Гамма-распределение - одна из основных статистических моделей для представления распределений случайных величин, ограниченных с одной стороны:

x³0, a>0, b>0, (3.9)

где

b - параметр формы,

а - параметр масштаба,

Г(b) - интеграл Эйлера первого рода:

(3.10)

Форма и масштаб кривых распределения зависят от величины и соотношения параметров а и b. Если b£1, то плотность гамма- распределения - убывающая кривая, если b>1, то распределение представлено одновершинной кривой с максимумом в точке (b -1)/ а.

Для практического вычисления параметров а и b используют метод моментов, дающий приближенные, но, как правило, вполне приемлемые результаты. Cреднее значение гамма- распределения M = b / a, а дисперсия s²= b / a ².

Вычислив на основании выборки значения M и s и приравнивая их соответствующим соотношением параметров, находим выборочные оценки а и b:

a = M / s ² , (3.11)

b = a M. (3.12)

Пример 3.4. Аппроксимируем при помощи гамма- распределения ряд распределения диаметра (из табл. 2.1) в среде пакета MS Excel. Для нашего примера a =18.36/34.22=0.5365, а b =0.5365×18.36=9.85. Далее используем встроенную функцию ГАММАРАСП().

Синтаксис функции:

ГАММАРАСП (x; альфа;бета;интегральная),

где

x - значение, для которого требуется вычислить распределение;

aльфа - параметр распределения, соответствующий b в (3.9);

бета - параметр распределения, соответствующий 1/a в (3.9);

интегральная - это логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция ГАММАРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

Сравнение эмпирических и вычисленных частот свидетельствует о неплохом соответствии принятой модели ряду распределений (рис. 3.4).

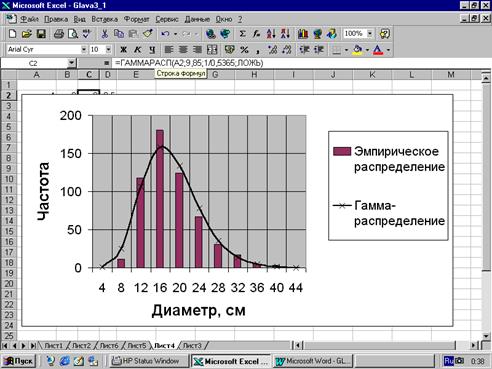
Рис. 3.4.

Бета-распределение

a>0, b>0, (3.13)

часто называют основным распределением для величин, ограниченных с двух сторон. Это удобная модель для многочисленных приложений, поскольку кривая бета- распределения может принимать самую различную форму в зависимости от величины параметров (рис. 3.5). Кроме того, посредством бета- распределения можно вычислять другие важные распределения. Если а > b >1 или b > a >1, то распределение одновершинное с максимумом в точке х =(а- l)/(a + b- 2) с левосторонней асимметрией в первом и

правосторонней во втором случае; если а <1, b <1, то распределение имеет U-образную, а при а ³1, b <1 I-образную форму. При а <1, b³1 кривая распределения убывающая. Если а = b, то распределение симметрично. В качестве примеров случайных величин, подчиняющихся бета - распределению, можно привести выработку бригады и др. за определенный

срок (смену, сутки), распределение большинства биометрических признаков деревьев и древостоев и др.

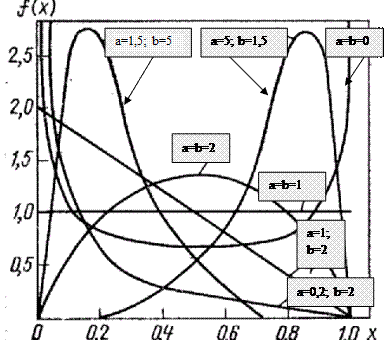Рис. 3.5

Выражение

называют В- функцией или интегралом Эйлера II рода. Так как В- функция выражается через Г-функцию, то ее обычно вычисляют при ручном счете по таблице значений Г-функции (Приложение 4).

Соотношения между параметрами бета - распределения и моментами, в частности средним и дисперсией, можно использовать для аппроксимации бета - распределения:

(3.14)

(3.15)

где

M - выборочное среднее;

s ² - выборочная дисперсия.

Формула плотности (3.13) задает бета- распределение на интервале [0,1]. В конкретных задачах интервал обычно ограничен некоторыми значениями [x₁,x₂]. В этом случае плотность задается следующей формулой:

a>0, b>0. (3.16)

Пример 3.5. Аппроксимируем при помощи бета - распределения ряд распределения диаметра (рис. 3.6) в среде пакета MS Excel. Имеем x1=0,54 и x2=0,78 (начало и конец ряда), среднее M=0,6596 и дисперсию s²=3,7712. Замена x '=(x -0,54)/(0,78-0,54) дает M '=0,4983, величина разряда с=0,02/0,24=0,0833, дисперсия s'²=(cs)²=0,02619. Для нашего примера b =(0,5017/0,02619)(0,4983×0,5017-0,02619)= 4,2873, а a =(0,4983/0,5017)4,2873=4,2582. Умножив (3.13) на n/c и прологарифмировав полученное выражение, получим

lg(n_i) =3,6459+3,2582 lg(x’_i)+ 3,2873 lg(1-x’_i).

Схема вычисления n _i по последнему выражению приведена на рис. 3.6.

Ряд распределения диаметра можно аппроксимировать и при помощи встроенной функции бета- распределения БЕТАРАСП() по аналогии с примером 3.4.

Синтаксис:

БЕТАРАСП (x;альфа;бета;A;B),

где

X - это значение в интервале между A и B, для которого вычисляется функция.

Альфа - это параметр распределения.

Бета - это параметр распределения.

A - это необязательная нижняя граница интервала изменения x.

B - это необязательная верхняя граница интервала изменения x.

Рис. 3.6.

Основные типы дискретных распределений.

Обычно дискретные распределения применяют как модели подгонки. Все они так или иначе связаны с вероятностями появления событий по схеме Бернулли: при проведении серии из п независимых испытаний в каждом из них может произойти либо не произойти событие Л. Вероятность события остается на протяжении всех испытаний постоянной и равна р. Представляют интерес и встречаются в практических приложениях многочисленные задачи, связанные со схемой Бернулли.

Date: 2016-07-25; view: 1526; Нарушение авторских прав