
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормальное распределение
|
|
Этот тип непрерывного распределения, открытого в 1733 г. Муавром, имеет плотность распределения:
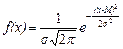 (3.1)
(3.1)
и функцию распределения (т. е. функцию накопленной вероятности):
 , (3.2)
, (3.2)
где
M - среднее значение;
s - среднее квадратическое отклонение.
Этими двумя параметрами нормальное распределение определяется однозначно, так как p =3,142… и е =2,718... - общеизвестные константы.
Графически плотность распределения f (x) представляет собой симметричную относительно точки х = M колоколообразную кривую, форма которой зависит от величины среднего квадратического отклонения s, являющегося параметром масштаба, а положение определяется величиной M (рис. 3.1). Кривая имеет один максимум 1/ 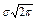 , две точки перегиба на расстоянии ± σ от M и асимптотически приближается к оси х на ±¥. Пользуясь формулами (2.2), (2.13), можно выразить моменты нормального распределения через его параметры. В частности, имеем m 0=1, m 1==0, m 2= σ 2, m 3=0 (нулю равны все нечетные моменты), m 4=3 σ 4. Поэтому равенство нулю показателей косости и крутости - необходимое и достаточное условие, чтобы некоторое распределение было нормальным.
, две точки перегиба на расстоянии ± σ от M и асимптотически приближается к оси х на ±¥. Пользуясь формулами (2.2), (2.13), можно выразить моменты нормального распределения через его параметры. В частности, имеем m 0=1, m 1==0, m 2= σ 2, m 3=0 (нулю равны все нечетные моменты), m 4=3 σ 4. Поэтому равенство нулю показателей косости и крутости - необходимое и достаточное условие, чтобы некоторое распределение было нормальным.
Закон нормального распределения играет особую роль как в теории статистического анализа, так и в его приложениях. Центральная предельная теорема утверждает, что распределение суммы независимых случайных величин (i=1,2,..., N) стремится к нормальному при неограниченном увеличении n, если все величины имеют конечные средние и дисперсии и ни одна из них по своему значению резко не отличается от других.
Непосредственное вычисление вероятностей по (3.1) и (3.2) было достаточно трудоемкой операцией в эру отсутствия ЭВМ. Для "ручного" счета составить таблицы для всевозможных значений x и M было практически невозможным делом. Поэтому применялись таблицы значений f (x) и F (x), составленные для так называемого нормированного распределения, в котором M =0 (перенос точки отсчета) и σ = 1 (изменение масштаба). Конкретное распределение «нормируют» путем замены переменных
z = (x - M)/σ, (3.3)
Определение вероятности попадания любого взятого наугад дерева в заданный интервал подтверждается примером 3.1.
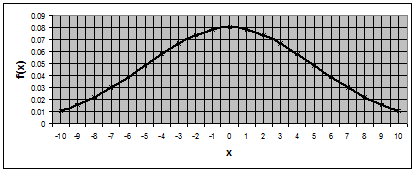

Рис. 3.1.
Пример 3.1. Диаметр деревьев в однородном древостое распределен по нормальному закону со средним M =35 см и s=6 см. Определить вероятность того, что наугад взятое дерево попадает в интервал: 1) 30…40 см; 2) M ±s, 3) M ±2s, 4) M ±3s.
Решим поставленную задачу с использованием пакета MathCAD. Для определения первой вероятности проинтегрируем (3.1) в пределах от 30 до 40:
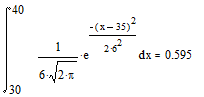 |
Таким образом, около 60% деревьев рассмотренного древостоя попадают в диапазон диаметров от 30 до 40 см. Аналогично производим расчеты для других трех случаев:
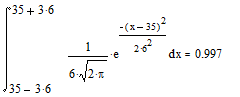 |
Последние расчеты демонстрируют справедливость так называемых правил "одной сигмы", "двух сигм" и "трех сигм". Можно доказать, что в выборке достаточно большого объема из нормальной совокупности в среднем 68% наблюдений не отличаются от значения среднего больше, чем на величину ±σ. Аналогично имеем р (M —2σ< х < M +2σ)=0,95, для M ±3σ -соответствующая вероятность - 0,997. Приведенное правило можно применять для приближенного решения ряда задач. Так, в большой выборке наименьшие и наибольшие значения случайной величины приближенно могут быть найдены как Х ±3σ (правило трех сигм).
Расчет теоретических частот эмпирического ряда производят следующим образом:
1. Находят значения функции плотности вероятности нормального распределения (Приложение 2) для соответствующих величин нормирован-ного отклонения (3.3);
2. Вычисляют теоретические частоты ряда распределения ni' по соответствующим данным объема выборки N, σ при величине классового промежутка i по формуле:
ni' = 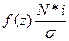 . (3.4)
. (3.4)
Наряду свычислением теоретических частот необходимо установить меру соответствия теоретически полученной кривой эмпирическому распределению по критерию χ2 Пирсона (Приложение 3).
Пример 3.2. Вычисление теоретических частот ni' и критерия соответствия эмпирического распределения нормальному χ2
| Xi | ni | z | f(z) | n’i | ni - n’i | (ni - n’i)2 | 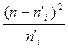
| |
| Факт. | Округ. | |||||||
| 2,07 | 0,04682 | 2,07 | ||||||
| 1,63 | 0,10567 | 4,66 | 0,2 | |||||
| 1,18 | 0,19886 | 8,78 | 0,11 | |||||
| 0,74 | 0,30339 | 13,39 | 0,08 | |||||
| 0,30 | 0,39876 | 17,61 | -2 | 0,22 | ||||
| 0,14 | 0,39505 | 17,44 | 0,06 | |||||
| 0,58 | 0,33530 | 14,81 | -1 | 0,07 | ||||
| 1,02 | 0,23713 | 10,47 | -1 | 0,1 | ||||
| 1,46 | 0,13542 | 5,98 | ||||||
| 1,91 | 0,06438 | 2,84 | ||||||
| 2,35 | 0,02522 | 1,11 | ||||||
| Σ | χ2 = 1,84 |
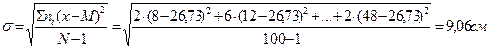
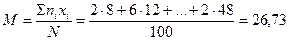 см
см
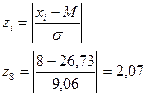
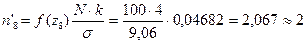
Cумма всех частных дает значение χ2 = 1,84 при (11-3) = 8 степенях свободы вариации. Табличное значение 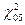 = 2, 73 (по табл. Приложения 3). Так как
= 2, 73 (по табл. Приложения 3). Так как 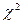 = 1,84 меньше
= 1,84 меньше 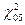 =2,7 3, то делаем заключение о подчинении распределения эмпирических частот закону нормального распределения.
=2,7 3, то делаем заключение о подчинении распределения эмпирических частот закону нормального распределения.
В целом предположение о том, что эмпирическое распределение строго соответствует нормальному закону, подтверждается относительно редко. Например, если в условиях, близких к требуемым по центральной предельной теореме, некоторые факторы влияют сильнее, чем другие, то распределение случайной величины становится несимметричным, хотя кривые распределения напоминают общие контуры нормальной кривой. Такие распределения (близкие к нормальным) обычны для лесного опытного дела. Далее рассмотрим одно из такого рода распределений – логарифмически нормальное.
Date: 2016-07-25; view: 714; Нарушение авторских прав