Сравнение частот взвешенных рядов по критерию

Колмогорова

При помощи критерия Колмогорова сравнивают лишь взвешенные ряды, как теоретические с эмпирическими, так и эмпирические между собой. Число наблюдений при этом должно быть достаточно большим, объединять их в очень крупные разряды (классовые промежутки) нельзя, а рассматриваемая случайная величина должна иметь распределение непрерывного типа.

Расчетное значение критерия Колмогорова К (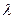) сравнивают с теоретическим значением для трех уровней доверительной вероятности 1,36 (Р₁=0,95); 1,63 (Р₂= 0,99); 1,95 (Р₃=0,999).

Если величина расчетного критерия меньше теоретического значения на 5-ти процентном уровне значимости, то различия считаются не существенными, если больше теоретического на однопроцентном уровне значимости, то устанавливается факт неслучайного (строгого) различия между двумя рядами распределения.

Критерий Колмогорова более удобен, чем критерий c-квадрат, в частности тем, что позволяет обходиться без таблиц теоретических значений c² и учета числа степеней свободы.

Пример 4.7. Вычисление критерия Колмогорова при сравнении частот эмпирического ряда с теоретическим, соответствующим кривой нормального распределения.

Ступень толщины
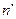
1	2	3	4	5	6	7	8
					0,02	0,02	0,00
					0,08	0,07	0,01
					0,18	0,16	0,02
					0,32	0,29	0,03
					0,48	0,47	0,01
					0,66	0,64	0,02
					0,80	0,79	0,01
					0,89	0,89	0,00
					0,95	0,95	0,00
					0,98	0,98	0,00
					1,00	1,00	0,00

d_max = 0,03

В столбце 8 вычислена разница без знака построчно между частостями эмпирического и теоретического рядов. Для дальнейших расчетов необходима лишь одна разность из этого столбца – максимальная, которая в данном случае равна 0,03. Рассчитываем значение критерия с объемом эмпирического ряда – N.

(4.10)

Полученное число меньше теоретического значения равного 1,36 при Р ₁ =0,95, поэтому делаем вывод, что кривая нормального распределения соответствует эмпирическому распределению.

Посредством критерия Колмогорова можно сравнить любые два эмпирических ряда.

Пример 4.8. Вычисление критерия Колмогорова при сравнении частот двух эмпирических рядов.

Ступень толщины	N1	N2	å n1	å n2
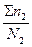
1	2	3	4	5	6	7	8
					0,02	0,02	0,00
					0,08	0,07	0,01
					0,18	0,16	0,02
					0,32	0,27	0,05
					0,47	0,44	0,03
1	2	3	4	5	6	7	8
					0,65	0,62	0,03
					0,79	0,77	0,02
					0,88	0,86	0,02
					0,94	0,92	0,02
					0,98	0,97	0,01
							0,01
	N1 = 341	N2 = 329					dmax = 0,05

Полученная в столбце 8 максимальная разность без знака подставляется в формулу расчета критерия

. (4.11)

Полученное число меньше критического значения, равного 1,36 при Р₁=0,95, что свидетельствует об отсутствии существенных различий между сравниваемыми эмпирических рядами распределения.

Date: 2016-07-25; view: 412; Нарушение авторских прав