Функции нескольких переменных

Пусть – множество упорядоченных пар действительных чисел .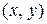

Определение 1. Если каждой упорядоченной паре чисел по некоторому закону поставлено в соответствие единственное действительное число , то говорят, что задана функция двух переменных или 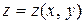. Числа называются при этом независимыми переменными или аргументами функции, а число – зависимой переменной.

Значение функции в точке 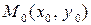обозначают 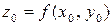или 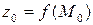и называют частным значением функции двух переменных.

Совокупность всех точек 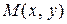, в которых определена функция , называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями. Например, область определения функции – вся плоскость, а функции 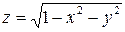– единичный круг с центром в начале координат ( или .

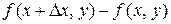Пусть задана функция двух переменных . Дадим аргументу приращение , а аргумент оставим неизменным. Тогда функция получит приращение , которое называется частным приращением по переменной х и обозначается :

.

Аналогично, фиксируя аргумент х и придавая аргументу прираще-ние , получим частное приращение функции по переменной :

.

Величина называется полным прира-щениием функции в точке .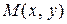

Определение 2. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю (если этот предел существует).

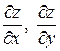Обозначается частная производная так: или , или .

Таким образом, по определению имеем:

,

.

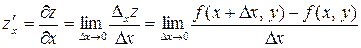Частные производные функции вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной х считается постоянной, а при дифференцировании по переменной постоянной считается х.

Пример 1. Найти частные производные функций:

а) ; б) .

Решение: а) Чтобы найти , считаем постоянной величиной и дифференцируем как функцию одной переменной х:

.

Аналогично, считая х постоянной величиной, находим :

;

б) ;

.

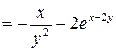Определение 3. Полным дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.

.

Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. , формулу полного дифференциала можно записать в виде

или .

Пример 2. Найти полный дифференциал функции .

Решение. Так как , то по формуле полного дифференциала находим

.

Частные производные и называют частными производными первого порядка или первыми частными производными.

Определение 4. Частными производными второго порядка функции называются частные производные от частных производных первого порядка.

Частных производных второго порядка четыре. Они обозначаются следующим образом:

или ; ил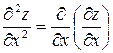и ;

или ; или .

Заметим, что в случае, когда смешанные производные непрерывны, то имеет место равенство .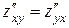

Пример 3. Найти частные производные второго порядка функции .

Решение. Частные производные первого порядка для данной функции найдены в примере 1:

. Дифференцируя и по переменным х и y, получим:

;

;

;

.

Определение 5. Точка 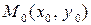называется точкой минимума (максимума) функции , если существует такая окрестность точки 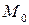, что для всех точек 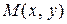из этой окрестности выполняется неравенство , ().

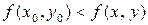Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).

Теорема 1 (необходимые условия экстремума). Если – точка экстремума дифференцируемой функции , то ее частные производные и в этой точке равны нулю: .

Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция может иметь экстремум, а может и не иметь.

Теорема 2 (достаточное условие экстремума). Пусть функция : а) определена в некоторой окрестности критической точки , в которо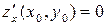й и ; б) имеет непрерывные частные производные второго порядка 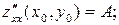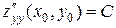. Тогда, если , то функция 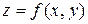в точке имеет экстремум: максимум, если А<0; минимум, если А>0; если , то функция 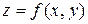в точке экстремума не имеет. В случае 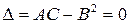вопрос о наличии экстремума остается открытым.

При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:

1. Найти частные производныепервого порядка: 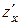и .

2. Решить систему уравнений и найти критические точки функции.

3. Найти частные производные второго порядка: , , .

4. Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.

5. Найти экстремумы функции.

Пример 4. Найти экстремумы функции .

Решение. 1. Находим частные производные и :

, .

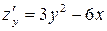2. Для определения критических точек решаем систему уравнений:

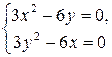или

Из первого уравнения системы находим: . Подставляя найденное значение y во второе уравнение, получим

, , ,

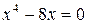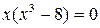откуда

.

Находим значения y, соответствующие значениям . Подставляя значения в уравнение , получим: .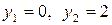

Таким образом, имеем две критические точки: и .

3. Находим частные производные второго порядка:

; ; .

4. Вычисляем значения частных производных второго порядка в каждой критической точке. Для точки имеем:

, , .

Так как , то в точке экстремума нет.

В точке : , , и, следовательно, . Значит, в силу достаточного условия экстремума, в точке функция имеет минимум, так как в этой точке и .

5. Находим значение функции в точке :

.

Date: 2016-07-25; view: 331; Нарушение авторских прав