НеоПРЕДЕЛЕННЫЙ иНТЕГРАЛ

Определение 1. Функция 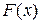называется первообразной для функции на интервале 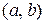, если она дифференцируема на 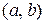и для любого выполняется равенство

.

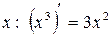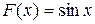Например, функция является первообразной для функции на всей числовой прямой, так как при любом значении , т. е. выполняется равенство ; функция является первообразной для функции 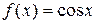на всей числовой прямой, так как в каждой точке .

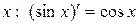Определение 2. Множество всех первообразных функций для функции 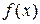на интервале 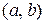называется неопределенным интегралом от функции 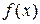на этом интервале и обозначается символом 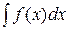, где – знак интеграла; – подынтегральная функция; 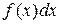– подынтегральное выражение; 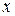– переменная интегрирования.

Таким образом:

,

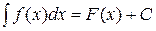где 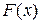– некоторая первообразная для на интервале 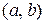; C – произвольная постоянная. Например, поскольку функция является первообразной для функции 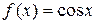, то .

Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию.

Date: 2016-07-25; view: 268; Нарушение авторских прав