
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Общая схема построения графика функции
|
|
1. Находим область определения функции.
2. Исследуем функцию на периодичность, четность или нечетность.
3. Исследуем функцию на монотонность и экстремум.
4. Находим промежутки выпуклости и точки перегиба.
5. Находим асимптоты графика функции.
6. Находим точки пересечения графика функции с осями координат.
7. Строим график.
Прежде чем перейти к примерам, напомним определения четности и нечетности функции.
Функция у = f (х) называется четной, если для любого значения х, взятого из области определения функции, значение (– х) также принад-лежит области определения и выполняется равенство f (х) = f (– х). График четной функции симметричен относительно оси ординат.
Функция у = f (х) называется нечетной для любого значения х, взятого из области определения функции, значение (– х) также принадлежит области определения и выполняется равенство f (– х) = – f (х). График нечетной функции симметричен относительно начала координат.
Пример 5. Построить график функции 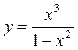 .
.
Решение:
1. D (у) = (–¥; –1) È (–1; 1) È (1; +¥).
2.  – функция нечетная. Следовательно, график функции будет симметричен относительно начала координат.
– функция нечетная. Следовательно, график функции будет симметричен относительно начала координат.
3. Исследуем функцию на монотонность и экстремум:

3 х 2 – х 4 = 0, х 2 · (3 – х 2) = 0, х 1 = 0, х 2 = 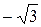 , х 3 =
, х 3 =  .
.
| х | (–¥;  ) )
| 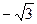
| (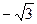 ; 0) ; 0)
| –1 | (–1; 0) | (0; 1) | (1;  ) )
| 
| ( ; +¥) ; +¥)
| ||
| у' | – | + | – | + | + | – | + | – | |||
| у | 
| 2,6 | 
| – | 
| 
| – | 
| –2,6 | 
|
min max
4. Исследуем функцию на выпуклость и точки перегиба:


х = 0 – точка, подозрительная на перегиб.
| х | (–¥; –1) | –1 | (–1; 0) | (0; 1) | (0; +¥) | ||
| у'' | + | – | – | + | – | – | |
| у | выпукла вниз | – | выпукла вверх | выпукла вниз | – | выпукла вниз | |
| перегиб |
5. Найдем асимптоты функции:
а) х = –1, х = 1 – вертикальные асимптоты.
Действительно:

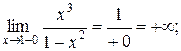
б) у = kx + b.
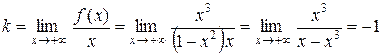 ,
,

Þ у = –1 х + 0 = – х – наклонная асимптота.
6. Найдем точки пересечения с осями координат:
х = 0 Þ у = 0 Þ (0;0) – точка пересечения с осями координат.
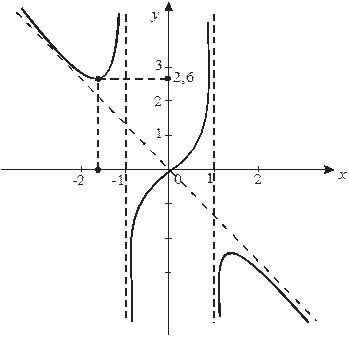
7. Строим график:
Date: 2016-07-25; view: 442; Нарушение авторских прав