
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Исследование функций
|
|
Пусть задана функция у = f (х) на множестве Х и х 0 – внутренняя точка множества Х. Обозначим через U (х 0) окрестность точки х 0. В точке х 0 функция f (х) имеет локальный максимум, если существует такая окрестность U (х 0) точки х 0, что для всех х из этой окрестности выполнено условие f (х) £ f (х 0).
Аналогично: функция f (х) имеет в точке х 0 локальный минимум, если существует такая окрестность U (х 0) точки х 0, что для всех х из этой окрестности выполнено условие f (х) ³ f (х 0).
Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них – локальными экстремумами функции.
Точками, подозрительными на экстремум функции f (x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х 0 = 0:

 f '(0) = 0 f '(0) $ f '(0) = ¥
f '(0) = 0 f '(0) $ f '(0) = ¥
Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f (x) дифференцируема в некоторой проколотой окрестности U (x 0) точки х 0 (проколотая окрестность означает, что сама точка х 0 выбрасывается из окрестности) и непрерывна в точке х 0, тогда:
1) если  (1)
(1)
то в точке х 0 – локальный максимум;
2) если 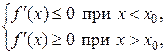 (2)
(2)
то в точке х 0 – локальный минимум.
Пример 1. Исследовать на монотонность и локальный экстремум функцию  с помощью производной первого порядка.
с помощью производной первого порядка.
Решение. Найдем стационарные точки функции:

Þ х 2 –1 = 0 Þ х 1 = –1, х 2 = 1.
Заметим, что данная функция не определена в точке х = 0. Следовательно:
| х | (–¥; –1) | –1 | (–1; 0) | (0; 1) | (1; +¥) | ||
| у' | + | – | – | – | + | ||
| у | 
| –2 | 
| – | 
| 
|
max min
то есть функция  возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке
возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке
х 1 = –1, равный у max (–1) = –2; имеет локальный минимум в точке х 2 = 1, равный у min (1) = 2.
Теорема 2 (второе достаточное условие экстремума). Пусть функция f (x) дважды непрерывно дифференцируема. Если х 0 – стационарная точка
(f '(х 0) = 0), в которой f ''(х 0) > 0, то в точке х 0 функция имеет локальный минимум. Если же f ''(х 0) < 0, то в точке х 0 функция имеет локальный максимум.
Пример 2. Исследовать на экстремум функцию  с помощью второй производной.
с помощью второй производной.
Решение. В примере 1 для данной функции мы нашли первую производную  и стационарные точки х 1 = –1, х 2 = 1.
и стационарные точки х 1 = –1, х 2 = 1.
Найдем вторую производную данной функции:

Найдем значения второй производной в стационарных точках:
 Þ в точке х 1 = –1 функция имеет локальный максимум;
Þ в точке х 1 = –1 функция имеет локальный максимум;
 Þ в точке х 2 = 1 функция имеет локальный минимум (по теореме 2).
Þ в точке х 2 = 1 функция имеет локальный минимум (по теореме 2).
Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая: равенство производной нулю, производная не существует, равна бесконечности в подозрительных на экстремум точках.
Теорема 3 (достаточное условие выпуклости). Если f (х) – дважды непрерывно дифференцируема на интервале (a, b) и
1) f ''(х) > 0,  х Î (a, b), то на (a, b) функция f (х) выпукла вниз;
х Î (a, b), то на (a, b) функция f (х) выпукла вниз;
2) f ''(х) < 0,  х Î (a, b), то на (a, b) функция f (х) выпукла вверх.
х Î (a, b), то на (a, b) функция f (х) выпукла вверх.
Точка х 0 называется точкой перегиба функции f (х), если $ d – окрест-ность точки х 0, что для всех х Î (х 0 – d, х 0) график функции находится с одной стороны касательной, а для всех х Î (х 0, х 0 + d) – с другой стороны касательной, проведенной к графику функции f (х) в точке х 0, то есть точка х 0 – точка перегиба функции f (х), если при переходе через точку х 0 функция f (х) меняет характер выпуклости.
Теорема 4 (необходимое условие существования точки перегиба). Если функция f (х) имеет непрерывную в точке х 0 производную f '' и х 0 – точка перегиба, то f '' (х 0) = 0.
Теорема 5 (достаточное условие перегиба). Если функция f (х) дважды непрерывно дифференцируема в окрестности точки х 0 и при переходе через точку х 0 производная f ''(х) меняет знак, то точка х 0 является точкой перегиба функции f (х).
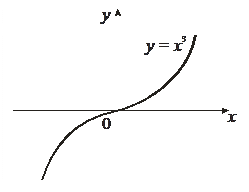 Пример 3. Исследовать на выпуклость и найти точки перегиба функции у = х 3.
Пример 3. Исследовать на выпуклость и найти точки перегиба функции у = х 3.
Решение: у' = 3 х 2, у'' = 6 х = 0 Þ х 0 = 0 – точка, подозрительная на перегиб.
В точке х 0 = 0 функция у = х 3 имеет перегиб:
| х | (–¥; 0) | (0; +¥) | |
| у'' | – | + | |
| у | выпукла вверх | выпукла вниз | |
| точка перегиба |
Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты.
Прямая х = х 0 называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов f (х 0 – 0) или f (х 0 + 0) равен бесконечности.
Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f (х) при х ® +¥ или х ® – ¥, если f (х) = kx + b + α(х),  , то есть если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® – ¥.
, то есть если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® – ¥.
Теорема 6. Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f (х) при х ® +¥ или х ® – ¥, необходимо и достаточно существование конечных пределов:
 (3)
(3)
Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.
Пример 4. Найти асимптоты функции  .
.
Решение:
а) функция неопределенна в точках х 1 = –1, х 2 = 1. Следовательно, прямые х 1 = –1, х 2 = 1 – вертикальные асимптоты данной функции.
Действительно, 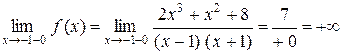 .
.
 ;
;
б) у = kx + b.


Следовательно, у = 2 х + 1 – наклонная асимптота данной функции.
Ответ: х 1 = –1, х 2 = 1 – вертикальные, у = 2 х + 1 – наклонная асимп-тоты.
Date: 2016-07-25; view: 370; Нарушение авторских прав