Основные правила дифференцирования

Теорема 1. Если функции u = u (x) и v = v (x) дифференцируемы в точке х, то функции u + v, uv, 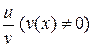дифференцируемы в этой точке, причем:

1) 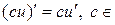R;

2)

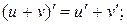
3) ;

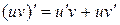4)

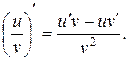
Теорема 2 (производная сложной функции). Если функция g (x) дифференцируема в точке х ₀, а функция f (у) дифференцируема в точке у ₀ = g (x ₀), то сложная функция f (g (x)) дифференцируема в точке х ₀ и

или .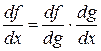

Таблица основных производных

1) с' = 0, с R;

2) х ' =1;

3) (хⁿ)' = nx^n-1, n R;

4) (а^х)' = а^х ln а, 0 < a ¹ 1;

5) (e^x)' = e^x;

6) 0 < a ¹ 1, х > 0;

7) х > 0;

8) (sin x)' = cos x;

9) (cos x)' = – sin x;

10) 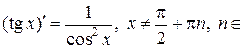N;

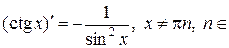11) N;

12) ;

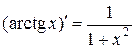13) ;

14) ;

15) .

Пример 3. Найти уравнения касательной и нормали к графику функции f (x)= 3 х ² + 4 в точке х ₀ = 2.

Решение

Найдем производную функции f (x): f ' (x) = 6 х.

Для того чтобы составить уравнения касательной и нормали (4) и (5), необходимо найти значения функции и ее производной в точке х ₀ = 2:

f (2) = 3 × 2² + 4 = 16,

f ' (2) = 6 × 2 = 12.

Следовательно, уравнение касательной имеет вид:

у = 12 (х – 2) + 16,

уравнение нормали:

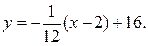
Ответ: у = 12 (х – 2) + 16,

Пример 4. Найти производные функций:

а) ;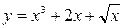

б) ;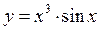

в) ;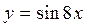

г) .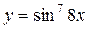

Решение:

а) ;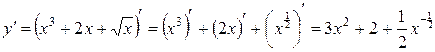

б) ;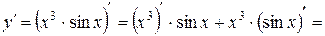

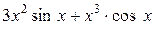в) ;

г)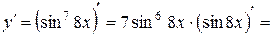

В примере г) мы вначале взяли производную степенной функции, затем производную sin 8 x, а в конце производную 8 х.

Логарифмическое дифференцирование.
Производная неявной функции.
Производные высших порядков

Логарифмическое дифференцирование применяют тогда, когда нужно найти производную выражения, содержащего произведения, корни, степени, то есть выражения, которое легко логарифмируется, а также для нахождения производной степенно-показательной функции u (x) ^{v ( x )}.

Пример 5. Найти производную функции:

а) ;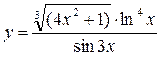

б) .

Решение:

а) прологарифмируем функцию у

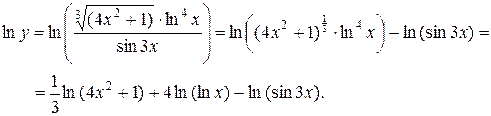
Находим производную левой и правой частей данного выражения, учитывая, что :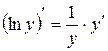

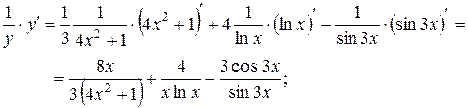
Þ

б) прологарифмируем степенно-показательную функцию 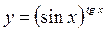(степенно-показательная функция – это функция, у которой функциями являются и основание, и показатель степени):

.

Находим производную левой и правой частей данного выражения:

.

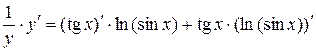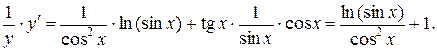
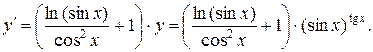
Функция называется заданной неявно, если она представлена в виде

F (x, y) = 0,

то есть «у» не выражен явно, или его, в принципе, нельзя выразить явно через х. В этом случае производная находится, учитывая, что «у» – функция. Например, .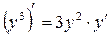

Пример 6. Найти производную:

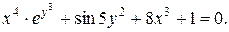
Решение

Продифференцируем данное выражение

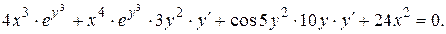
Þ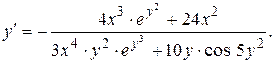

Второй производной от функции у = f (x) называется производная от ее первой производной у' = f ' (x). Обозначается вторая производная следующим образом: у'', f '', 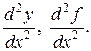Аналогично определяются производные третьего и более высоких порядков. Например, производная сотового порядка обозначается как у ⁽¹⁰⁰⁾ или .

Пример 7. Найти производные функции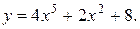

Решение:

у' = 20 х ⁴ + 4 х,

у'' = 80 х ³ + 4,

у''' = 240 х ²,

у ⁽⁴⁾ =

у ⁽⁵⁾ = 480,

у ⁽⁶⁾ = 0.

Заметим, что для степенной функции количество производных, отличных от нуля, равно наивысшей степени функции. В данном примере пять производных не равны нулю.

Date: 2016-07-25; view: 334; Нарушение авторских прав