Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
В. Метод интегрирования по частям
|
|
Пусть 
и 
– две дифференцируемые функции. По свойству дифференциала
,
или
.
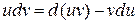Интегрируя обе части последнего равенства и учитывая, что 
, получаем
. (2)
Формула (2) называется формулой интегрирования по частям.
В некоторых случаях для нахождения искомого интеграла формулу интегрирования по частям приходится применять несколько раз.
Большая часть интегралов, берущихся по формуле (2), может быть разбита на три группы:
1. К первой группе относятся интегралы вида
, 
, 
, 
, 
, 
,
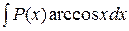где 
– многочлен. Для их вычисления следует применить формулу (2), полагая в ней 
равным одной из указанных выше функций, а 
.
2. Ко второй группе относятся интегралы вида
, 
, 
,
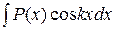где – многочлен; 
– некоторое число. Для их вычисления следует положить 
, а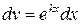 
, 
, 
соответственно.
3. К третьей группе относятся интегралы вида
, 
, 
, 
,
где 
и 
– некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям, причем за можно принимать любой из сомножителей. В результате получим уравнение первого порядка относительно исходного интеграла.
Пример 5
Date: 2016-07-25; view: 321; Нарушение авторских прав