Задачи для самостоятельного решения

Непрерывность функции в точке

1. Исследовать следующие функции на непрерывность в указанных точках:

а) б) .

2. Доказать, что функция f(x) = ax² + bx + c непрерывна в любой точке х ₀ Î R.

3. Найти точки разрыва следующих функций и определить их тип:

а) б)

4. Найти точки разрыва следующих функций:

а) ; б) .

ПРОИЗВОДНАЯ ФУНКЦИИ

Пусть функция f (х) определена в некоторой окрестности точки х ₀.

Производной функцииf (х) в точке х ₀ называется число, обозначаемое f ¢ (х ₀) и равное

, (1)

если этот предел существует.

Так как х = х ₀ + ∆ х, х – х ₀ = ∆ х, то предел (1) может быть записан в виде:

, (2)

то есть производная функции f (x) в точке х ₀ есть предел отношения ее приращения ∆ f (х ₀) в этой точке к соответствующему приращению аргумента ∆ х, когда ∆ х стремится к нулю.

Для обозначения производной функции f (x) в точке х ₀ используют следующие выражения:

.

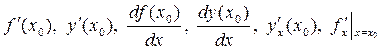Правой производной называется число

. (3)

Аналогично определяется левая производная .

Заметим, что существование производной функции в точке равносильно равенству ее односторонних производных в этой точке.

Пример 1. Используя определение производной, найти для функции f (x) = 4 x ² – 1.

Решение

Ответ: = 24.

Пример 2. Найти односторонние производные функции f (x) = | x | в точке х ₀ = 0.

Решение

Таким образом, функция f (x) = | x | в точке х ₀ = 0 не имеет производной, так как односторонние производные не совпадают.

Ответ: = 1, .

(4)

– уравнение касательной к графику f (x) в точке х ₀, причем,

,

где α – угол наклона касательной к положительному направлению оси 0 х.

Следовательно, с геометрической точки зрения, производная функции f (x) в точке х ₀ численно равна тангенсу угла, образованного касательной к графику функции f (x) в точке х ₀ и положительным направлением оси 0 х.

Прямая, перпендикулярная к касательной графика функции f (x) в точке , называется нормалью к кривой, определяемой функцией f (x), в точке х ₀. Учитывая, что для перпендикулярных прямых k ₁ k ₂ = –1, из (4) получаем уравнение нормали к графику функции f (x) в точке х ₀:

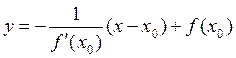. (5)

Операция вычисления производной функции называется дифференцированием. Функция, имеющая производную в точке, называется дифференцируемой в этой точке.

Date: 2016-07-25; view: 289; Нарушение авторских прав